撰文:luffy
最近,Paradigm 研究合夥人Dave White、Dan Robinson 與Uniswap 創始人Hayden Adams 一起合作設計了一個全新的做市模型「時間加權做市商TWAMM」(The Time-Weighted Average Market Maker)。根據其發表文章介紹,TWAMM 可以在以太坊上有效地交易大額訂單,工作原理是將長期大額訂單分解為無限多個無限小的虛擬訂單,在一定時間內使用嵌入式AMM 平滑地執行這些交易。
關於TWAMM 的虛擬交易所涉及的數學,Dave White 在文中並沒有多費筆墨,只在最後給出了非常簡單的數學結論,這對於理解TWAMM 的數學原理非常不利。本文將重點對TWAMM 的數學原理進行嚴格的論證和解釋,至於TWAMM 模型詳細的設計原理,可以前往Paradiagm 官網查看,本文不再做詳述。
定義
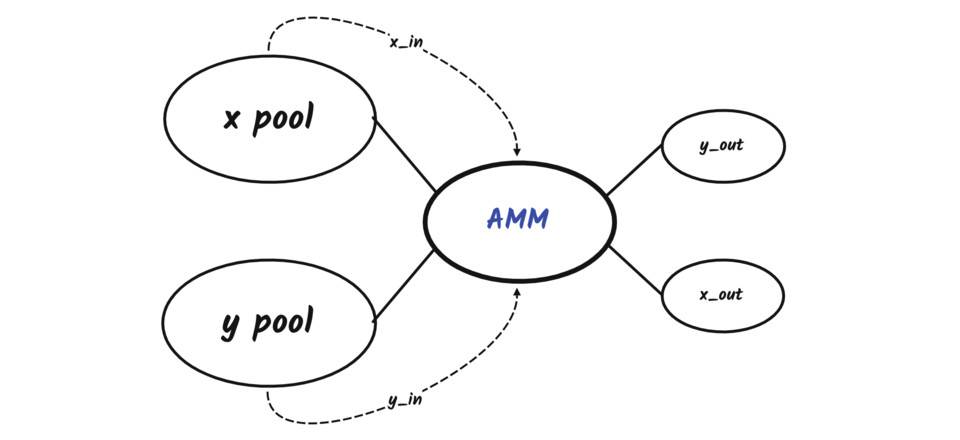
假設TWAMM 執行大額虛擬交易需要N 個區塊,出售X 的池子以每區塊xrate 的速率出售,而出售Y 的池子以每個區塊yrate 的速率出售。因此,在整個期間售出的X 總量為xin=Nxrate,售出的Y 總量為yin=Nyrate。
同時,我們將此時間段嵌入AMM 的初始儲備xreserve 和yreserve 分別表示為x0=xammStart 以及y0=yammStart。
按照TWAMM 的設計,大額訂單是隨著區塊進行交易的,每個區塊出售xrate 得到yout,或者出售xrate 得到yout,同時AMM 會更新xreserve 和yreserve 的值,整個過程總共交易N 次。
值得注意的是,AMM 的每個區塊交易總是遵循恆定乘積做市。
官方的
首先,在執行第n-1 區塊的交易後,我們假設此時AMM 的xreserve 和yreserve 值分別為xn-1 和yn-1。
接下來執行第n 區塊的交易,X-Pool 和Y-Pool 分別向AMM 輸入xrate 和yrate,命:
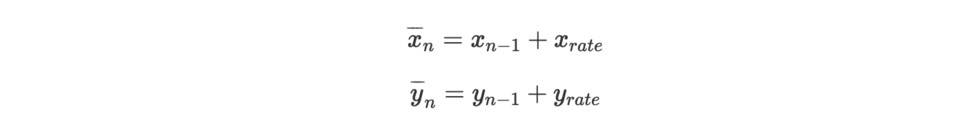
因為xrate 和yrate 非常微小,且區塊的交易AMM 遵循恆定乘積做市商,我們可以得到,
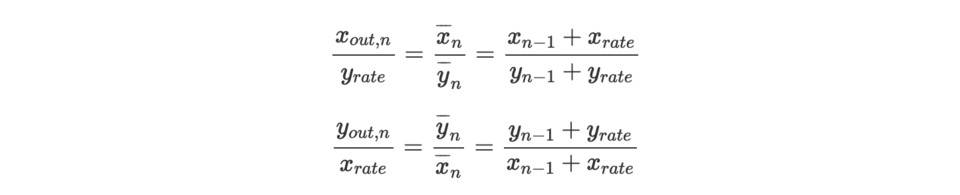
化簡,
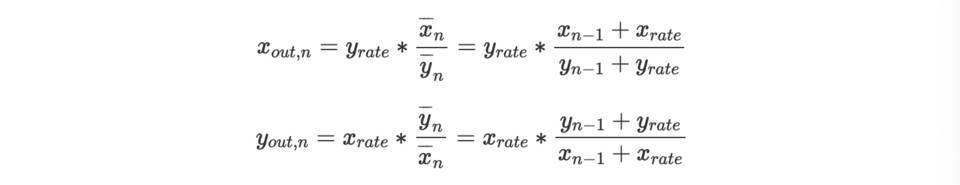
在得到xout,n 和yout,n 的值後,我們進一步可以獲得n 區塊的交易後AMM 的xreserve 和yreserve 值xn 和yn,
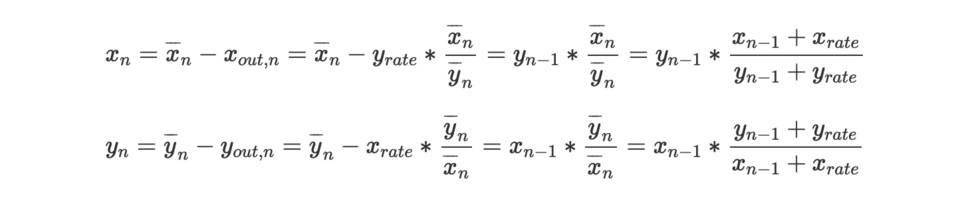
通過觀察,我們發現xn*yn=xn-1*yn-1,這正好符合AMM 的循恆定乘積做市的前提要求。
令, xn*yn=xn-1*yn-1=…= x1*y1=x0*y0=k,這是一個常數。
分式線性遞歸
先對xn 求得一般公式,並獲得xammEnd=xN 的值,yn 同理。
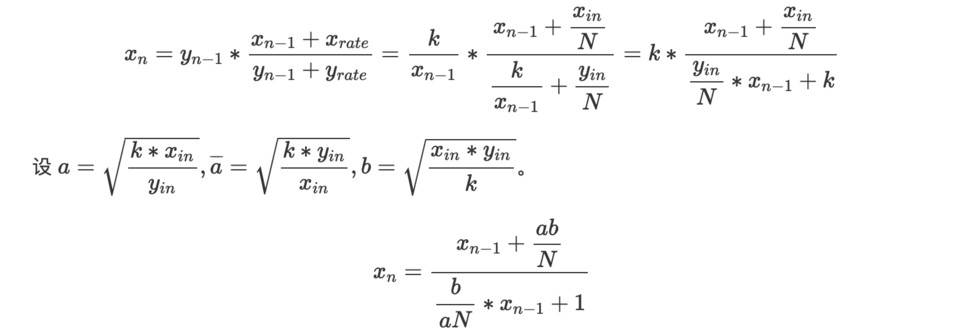
yn 的分式線性遞歸表達式如下:
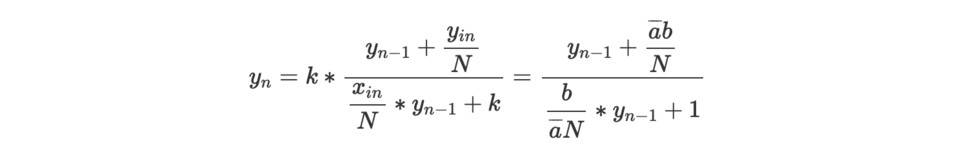
解
首先,若yin 等於0,xin 不等於0,則
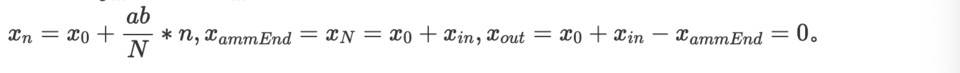
而
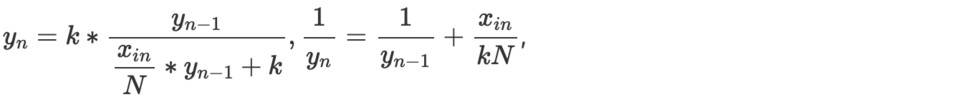
計算得到,
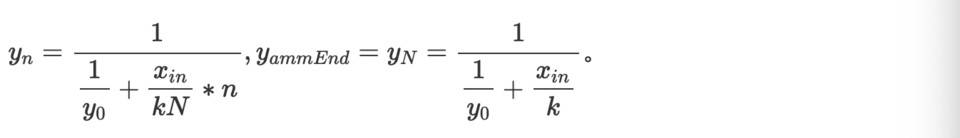
而,
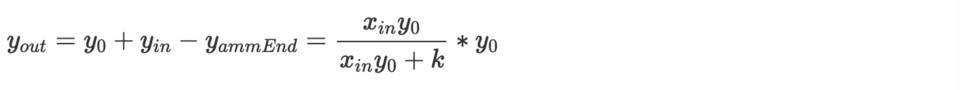
xin 等於0,yin 不等於0 時,討論同上。
若xin 和yin 都不等於0,對於一般的分式線性遞歸,我們可以採用不動點的方法求解。
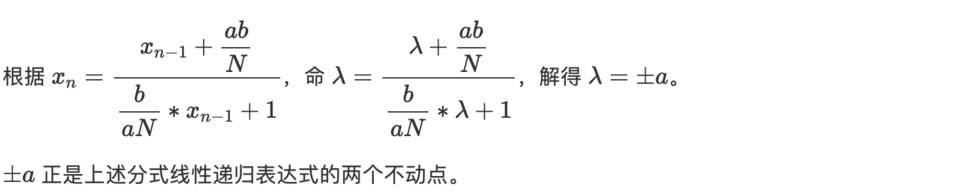
進一步計算,
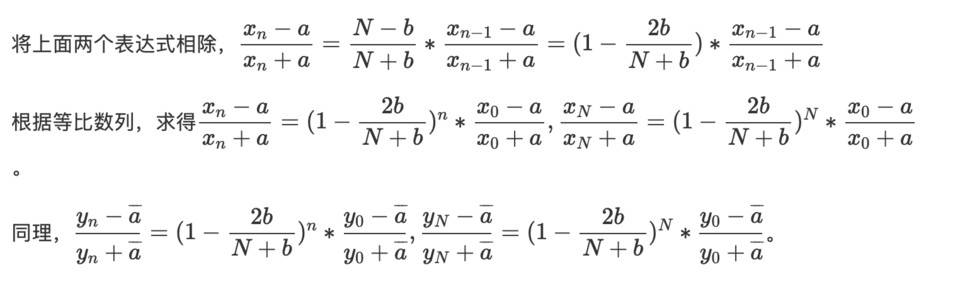
極限
TWAMM 的基本假設是將長期大額訂單分解為無限多個無限小的虛擬訂單,也即是N 可以取無窮大,這時候可以獲得xN 的極限值。
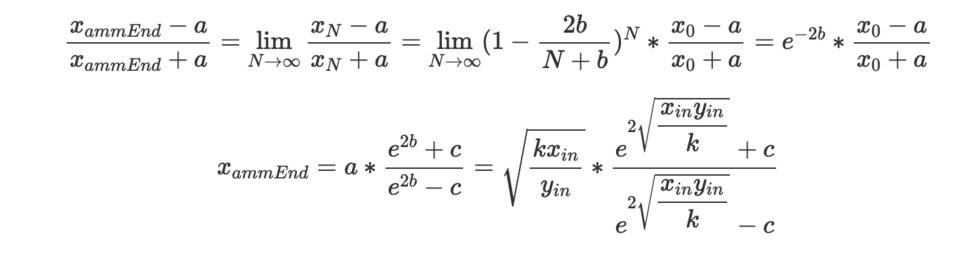
其中,
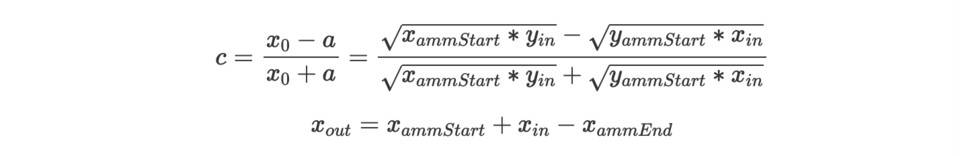
相似的,
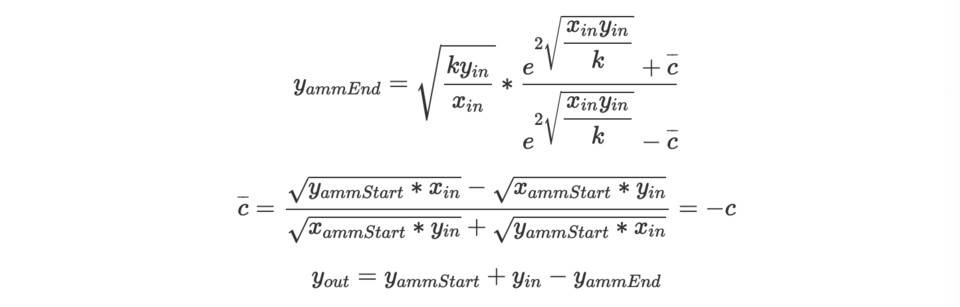
最後,經過簡單的驗證xammEnd*yammEnd=xammStart*yammStart=k, 依然滿足AMM 的恆定乘積。
至此,我們完成了TWAMM 的數學原理嚴格的論證和解釋,並得到了與 「時間加權做市商TWAMM」 一文完全相同的結論。