基於哈希的密碼學:通往量子安全的數學路徑(下)
八、一次性簽名方案
一次性簽名(OTS)方案是由三種算法組成的:一種用於生成一次性密鑰對,一種用於計算一次性簽名,還有一種用於簽名驗證。一個OTS方案的實例有一個特定的密鑰對(P,S),其中P是公鑰,S是私鑰。
OTS方案和Merkle樹(如下所述)都使用哈希函數。一個重要問題是,同一哈希函數是否可以安全地用於這兩種結構。事實上,通過在每個哈希中包括一點額外的數據(這被稱為域分離domain separation),我們基本上可以把一個散列函數當作許多不同的散列函數。換句話說,如果我們使用SHA-256來生成OTS實例,我們仍然可以安全地使用SHA-256來構建Merkle樹。
多次或完整,基於哈希的簽名方案使用哈希樹來有效地結合OTS方案的許多實例。
九、基於哈希的密碼學是如何工作的?
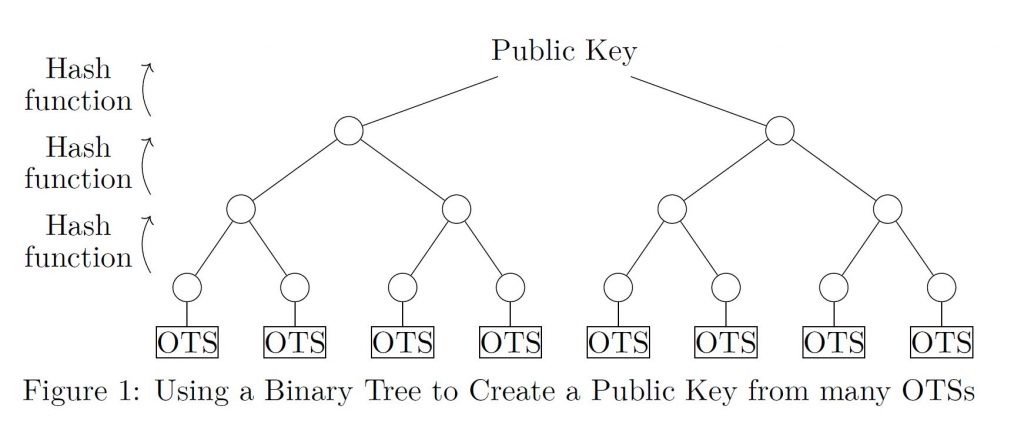
我們現在將討論Merkle如何使用二進制樹-如圖1所示的二進制樹-結合許多個OTS來創建一個基於哈希的多次簽名方案的公鑰。雖然從這些OTS中構建樹的初始步驟(可以離線完成)與許多其他抗量子的構建相比通常很慢,但簽名卻很快。
十、二叉樹
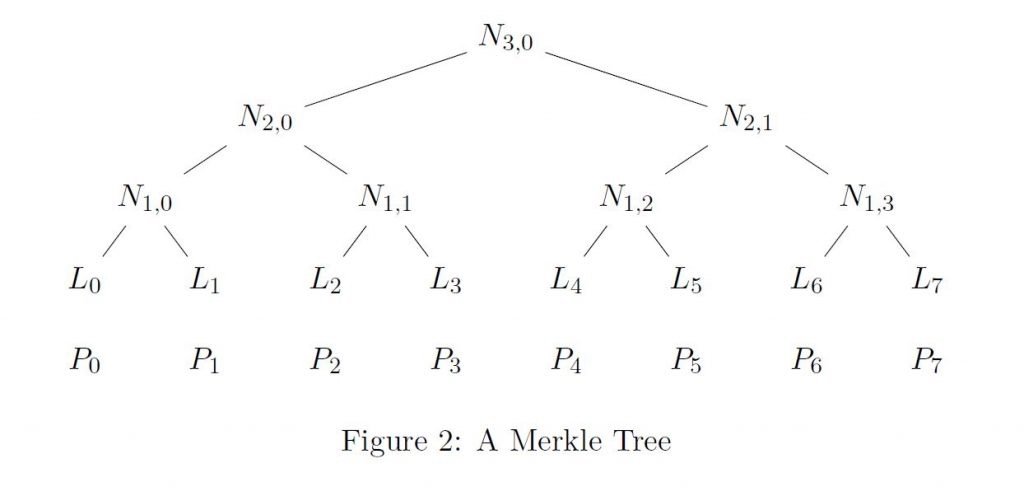
在一棵標準的二叉樹中,所有的節點(除了最上面的節點)都是成對出現的,它們上面有一個節點,從最下面的節點到最上面的節點的距離總是相同的。另一個節點的正上方是其父節點,父節點的正下方是其子節點,一對具有相同父節點的子節點被稱為兄弟姐妹節點。例如,在圖2和圖3中,N(1,0)和N(1,1)是兄弟姐妹節點。它們也是N(2,0)的子節點;也就是說,N(2,0)是它們的父節點。
最上面的節點被稱為根節點。樹的底部沒有子節點的節點被稱為葉節點。葉節點表示為L0, …. ,圖2中的L7。
一個節點的級別是它與底部的距離。我們的意思是葉子節點有0級,圖2中的節點N(j,i)有j級。根節點的級別,通常表示為h,稱為樹的高度。例如,圖2中的樹的高度為3。 Merkle使用二進制樹來組合OTS,更具體地說:每個葉子節點來自一個(不同的)OTS實例的公鑰,而樹上的每個其他節點都是由它的兩個子節點計算出來的。我們現在將描述這些節點是如何使用加密散列函數計算的。
十一、加密哈希函數(Cryptographic Hash Functions)
簡單地說,加密哈希函數H是一個將任意數量的數據映射到一個合理的、通常是固定長度的輸出的函數,在這種情況下,實際上不可能找到一個映射到特定輸出的輸入(或兩個給出相同輸出的輸入)。
直觀來講,我們可以認為默克爾樹是使用哈希函數將一個有序的數值集壓縮成一個單一的數值,其方式是很容易證明一個數值屬於原來的數值集。更具體地說,Merkle樹可以從O的公鑰的一個有序集合P0 …Pm的OTS的公鑰和哈希函數H,以如下方式構造:
- 每個葉子節點是一個OTS公鑰的哈希輸出。換句話說,讓底部一行的第i個條目為L(i) = H(P(i));見圖2。
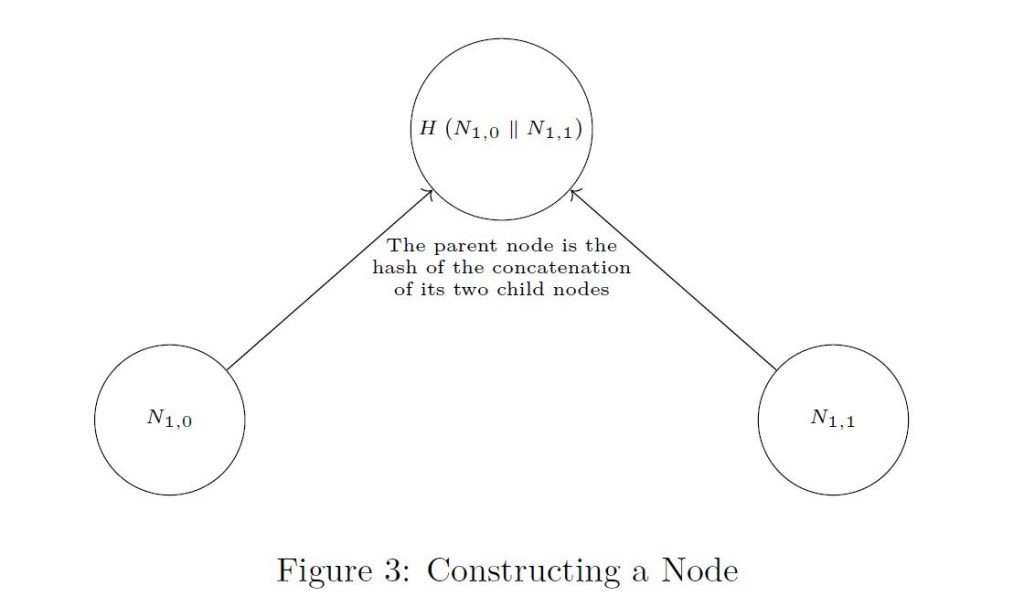
- 樹上的每一個其他節點都是其兩個子節點的哈希值(連接)。例如,如圖3
N(1,0) = H(L(0) || L(1)) 和 N(2,1)= H(N(1,0) || N(1,1))
通用表達如下:
N(1,i)= H(L2(i) || L2(i+1)) and N(j+1,i)= H(N(j,2i) || N(j,2i+1)) )
Merkle簽名算法的公鑰是根節點。在圖2中,根節點(公鑰)是N(3,0)
哈希樹是Merkle樹的一個概括,其中P(i)是任意數據而不是OTS公鑰,見圖2。
由於你無法找到哈希函數的逆運算,所以實際上不可能從樹中較高的節點中找到樹中較低的節點。因此,給定樹中的任何一組節點,特別是給定根節點,都不可能找出關於OTS簽名鑰匙的信息。
十二、驗證路徑
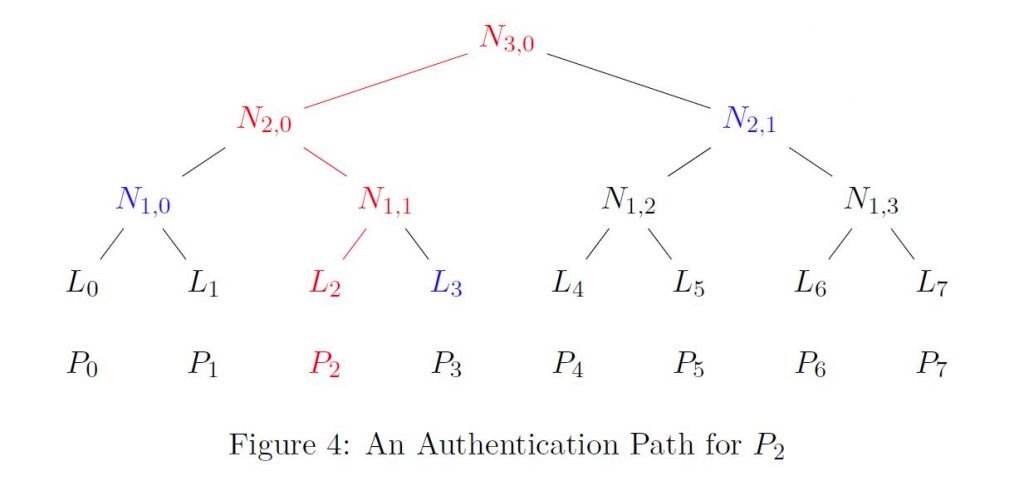
請注意,對於任何用於創建Merkle樹的P(i),都有一條從葉子節點L(i)到根節點(公鑰)的唯一路徑。例如,在圖4中,從L(2)到頂部的路徑是用紅色畫的。給定P(i),如果你能構建一個這種形式的路徑,那麼這幾乎可以肯定地證明P(i)是用來創建Merkle樹的值之一。這源於這樣一個事實,即找到具有特定輸出的哈希函數H的輸入在計算上是不可行的,因此你不能從樹中較高的節點找到樹中較低的節點。
然而,我們實際上是利用葉子到根的路徑節點的同級節點來檢查路徑是否被合法地構建。出於這個原因,我們引入了P(i)的認證路徑的概念,即從L(i)到根節點的路徑中的兄弟節點的有序集合。在圖4中,P(2)的認證路徑(藍色)是L(3), N(1,0), N(2,1)。給出P(i)(一個OTS的公鑰),以及P(i)的認證路徑,我們可以驗證(認證)P(i)對應的是一個葉子節點。也就是說,如果P(i)確實被用於生成樹,那麼鑑於認證路徑,重建從P(i)到根節點的路徑應該很簡單。
參照圖4,我們可以證明P(2)被用來創建Merkle樹的公鑰,只需給它的認證路徑(藍色)L(3), N(1,0) , N(2,1),通過構建一個從P(2)到根節點(公鑰)的路徑。
要做到這一點,我們只需檢查值:
H(P(2)), H(L(3) || H(P(2))), H(N(1,0) || H(L(3) || H(P(2)) )), H(N(2,1) || H(N(1,0) || H(L(3) || H(P(2)))))
給出一個路徑,其中最後一個值H(N(2,1) || H(N(1,0) || H(L(3) || H(P(2))))) 是多次簽名算法的公鑰(即根節點)。由於P(2)實際上是用來構建Merkle樹的,所以構建H(N(2,1) || H(N(1,0) || H(L(3) || H(P(2))))) = N(3,0)。
如果上述計算得到了公鑰,那麼我們就證明了P(2)是最初用於創建哈希樹的OTS密鑰之一(因為找到一個非法的認證路徑需要解決尋找哈希函數的反圖像這一計算上難以解決的問題)。
十三、基於狀態哈希的簽名方案一覽
多次方案的一般構造總結如下。
- 密匙生成(Secret Key Generation)
- 創建m = 2^h個OTS公私鑰對(Pi, Si)。直觀地講,我們可以認為多次秘鑰(many-time scheme)是生成OTS密鑰對所需的材料。
- 公鑰生成(Public Key Generation)
- 為P1,……,Pm創建如上所述的哈希樹,根節點是基於哈希的簽名方案的公鑰。
- 簽名(Signatures)
- 為了簽署一個信息,選擇一個以前從未使用過的索引i。用Si(OTS簽名密鑰)對消息進行簽名,得到一次性簽名,併計算出Pi的認證路徑。該信息的簽名是一次性簽名以及Pi的認證路徑。
- 驗證(Verification)
- 為了驗證一個消息的簽名,我們首先使用消息和運行一次性驗證方案。接下來,檢查Pi的認證路徑是否提供了一個從Pi到基於哈希的簽名的公鑰(根節點)的有效路徑。如果是這樣,則接受該消息和簽名為真實的。
- 時間/空間的權衡(Time/Space Tradeoffs)
- 由於樹可以從P1 …Pm生成,存儲整個樹並不總是必要的。決定存儲多少樹以及如何管理樹,會導致各種CPU/內存等資源消耗的權衡。此外,所有的密鑰P1…Pm也可以從一個單一的短種子再生,進一步減少所需的長期存儲量。
- 簽名的數量(Number of Signatures)
- 如果樹的高度是h,那麼它可以用來簽署多達2^h的信息。
- 有狀態的簽名(Stateful Signatures)
- 由於每個OTS簽名密鑰最多只能使用一次,在一個有狀態的基於哈希的簽名方案中,跟踪哪些一次性密鑰對被使用是很重要的。
參考文獻:
[1] David Cooper、Daniel Apon、Quynh Dang、Michael Davidson、Morris Dworkin 和 Carl Miller。 基於有狀態散列的簽名方案的建議。 技術報告,美國國家標準與技術研究院,2019 年。
[2] 安德烈亞斯·赫爾辛等人。 SPHINCS+。 NIST 後量子密碼標準化第 2 輪提交,2019 年。
[3] A Hülsing、D Butin、S Gazdag、J Rijneveld 和 A Mohaisen。 XMSS:擴展默克爾簽名方案。 加密論壇研究組 RFC。 rfc-editor.org/info/rfc8391,2018 年。
[4] 大衛·麥格魯、邁克爾·庫西奧和斯科特·弗魯勒。 基於 Leighton-Micali 哈希的簽名。 加密論壇研究組 RFC。 rfc 編輯器。 組織/信息/rfc8554,2019。
[5] 拉爾夫·默克爾。 保密、認證和公鑰系統。 博士論文,斯坦福大學,1979。
展開全文打開碳鏈價值APP 查看更多精彩資訊