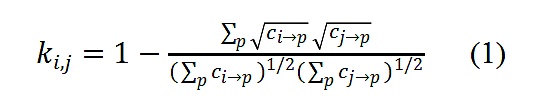背景介紹
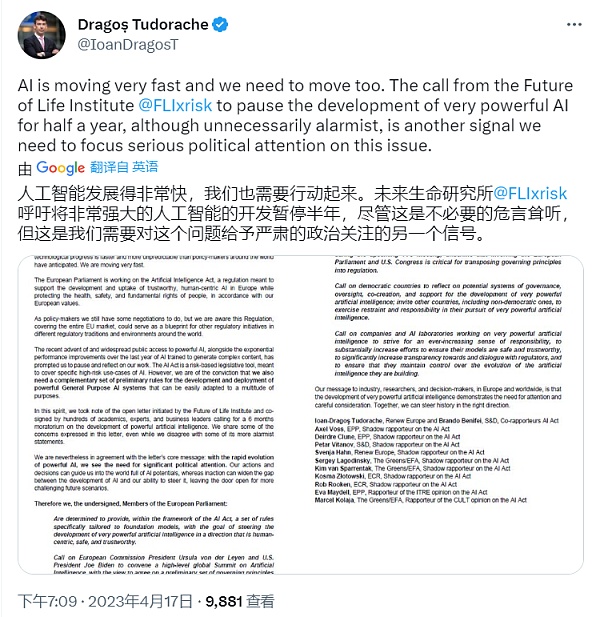
自2018年以來,Vitalik一直主張二次方融資(QF)作為一種在去中心化的、自組織的生態系統中生成最優公共產品供應的方法(Buterin、Hitzig和Weyl, 2018)。 QF面臨的最具挑戰性的問題之一是共謀。例如,一個參與者或一組協調的參與者可能控制多個地址或共謀“遊戲系統”,並在QF中提取不合理的補貼。
自2019年以來,Gitcoin Grants已經運行了多輪的QF。 Gitcoin Grants使用了一種創新的方法:雙界協調補貼(pairwise-bounded coordination subsidies)(Buterin,2019)。然而,Zoudavid認為Buterin(2019)中的不協調係數(discoordination coefficient)的說明不是很直觀,也不太令人信服。此外,Buterin(2019)中的可調整參數(tweakable parameter)主要用於約束任何一對投資者的可提取價值,但在調整他們之間的共謀方面做得不夠。在《關於改善配對協調補貼的提議》(A Proposal to Improve Pairwise Coordination Subsidies)一文中,Zoudavid提出了一種新的方法來改進具有豐富經濟意義的配對協調補貼(pairwise coordination subsidies)。
不協調係數的一種新規範
採用Buterin(2019)的符號,Zoudavid提出了一種新的不協調係數的規範:
其中
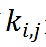
是向量i和j的不協調係數,
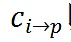
以及
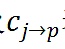
表示投資者i和j對項目p的投資,
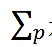
是所有項目的總和。不協調係數衡量的是衡量的是一對投資者在作出投資決策時的獨立性。有兩種視角來理解等式(1)的經濟含義。
一種視角是,考慮兩個向量
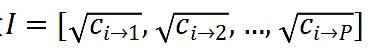
以及
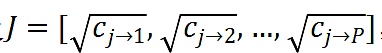
,其中p表示項目的總數。
令
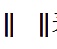
表示向量的模:
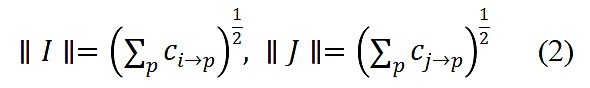
令
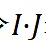
表示兩個向量的內積,
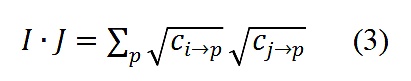
令
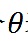
表示兩個向量之間的角度,則有,
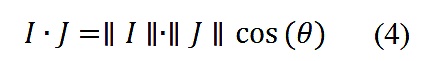
如果這兩個向量是正交的(如,
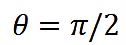
),那麼
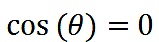
並且
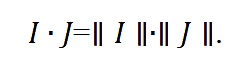
從(1)-(4),很容易可以看出,
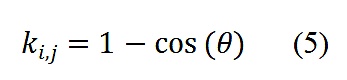
對於(5)來說,先考慮兩種比較極端的案例。
案例#1:對於每一個p,
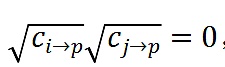
,這意味著和沒有共有的投資,這就符合
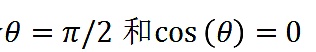
和
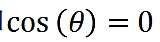
(如,正交的向量)。在這個例子中,
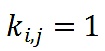
,意味著i和j有最大的不協調性。
案例#2:如果存在一個
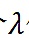
使得對於每一個p,有
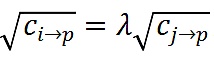
,這意味著i和j做了同樣的投資決策。儘管他們可能有不同的投資金額,但有相同的資產配置決策的百分比。這符合
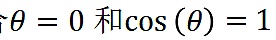
的情況(如,同一方向的向量)。在這種情況下,
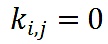
,也就是和有最大的協調性。
其他的例子都落在案例#1和#2之間:
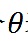
0 總和
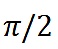
之間,
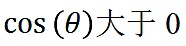
小於1。因此,
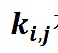
在0到1之間。
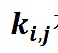
越大,不協調性越大。
另外一種視角是從概率論的角度理解
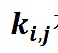
的含義。在事前,每個投資者的投資決定都是一個隨機變量。因此,向量
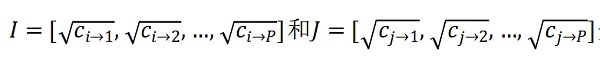
分別是i和j的事後現實的投資決策。在等式(1)中,
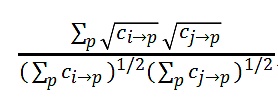
只是對他們的投資決策之間的相關係數進行了抽樣估計。協調係數越大,不協調係數就越小。
不協調係數調整後的補貼
對於項目p來說,在協調調整過i和j的補貼是
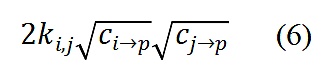
當
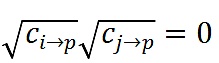
或者說i和j是完美協調(perfect correlated)時,這個補貼為0。
從等式(6),Zoudavid定義了i和j從所有項目中提取的不協調係數調整後的補貼(discoordination adjusted subsidy,DAS)為
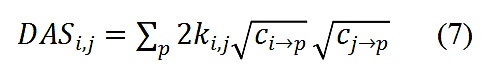
值得指出的是,要用(1)估計
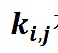
,可以使用前幾輪二次方融資的樣本數據,而不僅僅是本輪。這樣,可以使不協調係數的估計更穩健,並減少對當前樣本量的限制。
對配對邊界的調整
假設對於任何一對投資者從所有項目中提取的總補貼引入一個上限。設B是普遍適用的上限。 B類似於Buterin(2019)中的可調整參數。
給
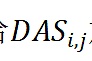
加上上限B:與Buterin(2019b)相似,Zoudavid使用了下面的公式:
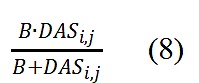
顯然,
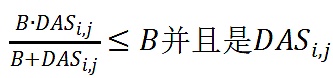
。同樣與Buterin(2019)類似T,如果存在總補貼的特定水平,需要在滿足下列約束的情況下求解出B(N是投資者總數):
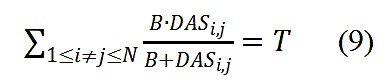
用數值方法不難求出等式(9)的解。
與現有方法相比
考慮一種情況:i和j做出了同樣的投資決策(如,存在一個
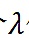
使得對於每一個p,有
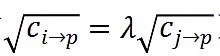
)。用Zoudavid的方法,他們將不會得到任何補貼。但用目前的方法,他們可以獲得大量的補貼,只是被可調整的參數所縮減。
用Buterin(2019)中描述的景象舉例。假設k個經過協調的代理人都向一個項目貢獻了一筆很大數額的資金w。由於他們是完美協調的,用Zoudavid的方法他們可以提取的資金是0。然而,用現存的方法他們可以提取的資金是
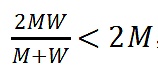
,其中M是可調整的參數。
Vitalik建議了這樣一種情況:假設有兩個贈款者A和B和三個項目A,B和C,其中有相同字母的捐贈者和項目對是相互串通的。現在假設A捐贈了X 0 X,以及B捐贈了0 X X。
在這個例子中,
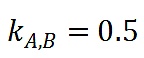
。如果使用過去幾輪二次方融資的數據,
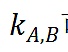
可能會有不同的估計,而且可能會更準確。
不協調係數調整後的補貼是
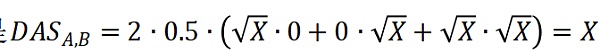
,這正好是當前方法的一半水平。在把上界納入考慮之後,總的補貼是。用當前方法,總的補貼是
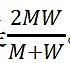
。
從上面的例子中可以清楚地看到,在當前的方法中,沒有對不協調的調整,只有對邊界的調整。
針對該方法的多方觀點
(1)優勢
Vbuterin認為該提議是非常有趣的洞見,其有趣之處在於用點積(dot product)來直接估計多個協調者之間的不相關關係。
(2)存在的不足
一方面,Vbuterin認為,本質上來說,任何一個代理人A總是可以通過簡單地創建一個項目並對他自己和代理人B進行一筆大金額的捐贈來提高他和B的不協調係數。如果每一個A都創建一個項目
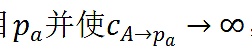
,那麼其點積就不會受到任何影響。因為不會有其他的人向
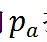
捐贈,但這會增加他們的
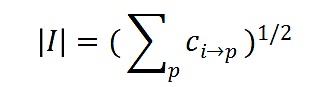
價值到無限大,使得分式為0並且對於所有的j
來說
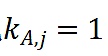
。
Vbuterin提出了約束的相關係數(bound-based correlation coefficient),其屬性是,兩個參與者向同一個項目捐贈會增加他們的相關分數(correlation score),但兩個參與者向不同的項目捐贈不會減少他們的相關分數。他認為如果Zoudavid想有一個系統,其中兩個參與者捐贈給不同的項目將減少他們的相關分數,那麼需要以某種方式擊敗發送至自身的攻擊(send-to-self attack)。
而Zoudavid有針對性地提出,發送至自身的攻擊(send-to-self attack)並不會帶來很大的問題。並給出了三點理由。
首先,自發送攻擊代價高昂,因為攻擊者需要在他的“假”項目中鎖定大量資金。而與此同時,其回報將是有限的。假設攻擊者創建了一個只有他投資而沒有其他投資者投資的項目。的確,通過增加對這個項目的投資,他可以增加對他和其他投資者之間相關性的估計。然而,他可以從他的“假”項目中提取的補貼仍然是0。對於其他項目,由於攻擊而增加的補貼應該是非常有限的,而且這種增加不能被攻擊者獨享。
其次,在計算不協調係數時,可以簡單地排除任何只有一個投資者的項目。例如可以認為這些項目融資失敗,沒有資格獲得QF補貼。在法幣眾籌中,通常有一個門檻機制:任何一個項目在一定時間內無法獲得足夠的支持或資金承諾將被認為是失敗的,之後任何資金承諾將被返還。 Zoudavid認為QF可以納入類似的機制。
最後,可以利用前幾輪QF的數據來估計不協調係數,使其估計受單個數據點的影響更小。
另一方面,Peter Watts察覺到協調懲罰(Coordination penalties)似乎依賴於一個假設:誠實的用戶會將資金分散到多個項目中,完美地反映出他們的偏好(即按比例為每個他們將獲得價值的項目提供資金)。而實際上,他懷疑許多用戶會因為方便或強烈的偏好而只投資一小部分。因此,真正的公共產品將會有很多高度相關的資助者,而得不到足夠的補貼。
(3)進一步探討
Vbuterin提出了一個方法,就是將重點再移開一步,不關注項目本身,而是關注向同一項目捐贈的一對捐贈者,並提出用3條規則來判斷:
1. 如果代理人i和j都向項目p捐贈那麼他們是更加相關的;
2. 如果代理人i和j都向項目p和q捐贈,而存在某個代理人k也是都捐贈了p和q,那麼i和j是更加相關的;
3. 如果代理人i和j都向項目p和q捐贈,而存在某個代理人k只捐贈了p或者q中的一個,那麼i和j的相關性變弱。
規則(3)將在所有代理中進行匯總,因此,捐贈給你自己的項目比捐贈給其他100人也捐贈的項目所帶來的不相關要少得多。
Vbuterin提出用更複雜的矩陣乘法的使用來描述這個問題。如果M是一個(非正方形)矩陣,將個人貢獻的平方值映射到項目上,那麼
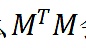
會給出個人之間的原始相關性,然後可以做一些其他的事情來計算出高階測量,但是這個方法需要進一步考慮。
針對Vbuterin“高階相關測度(higher-order measures of correlation)”的建議,Zoudavid做了一些初步的研究。基本上,除了不同投資者之間的相關性,還應該考慮不同項目之間的相關性。就像協調的投資者傾向於做出相似的投資決策一樣,相關的項目也傾向於吸引相似的投資者群體。在利用投資數據估計投資者之間的相關性時,應該意識到項目之間的相互依賴性。對於此,Zoudavid提出奇異值分解(Singular Value Decomposition,SVD)是研究這一問題的合適工具。然而,該解決方案可能過於復雜,難以與投資者社區溝通。此外,解決方案可能容易過擬合。
Peter Watts認為當試圖減少欺詐時,最重要的是不要失去CLR的核心租戶。在完全基於協調懲罰的局部最大值確定之前,可能還有更多的機制可以探索,要么補充協調懲罰,要么取代它們。衡量成功的標準不應僅僅是減少欺詐的程度,還應是資金分配到真正的公共產品的程度。針對這個問題,他提出了幾個想法:
負的偏好(Negative preferences)
對於每個用戶來說,項目實際上可以分為三類:
A)我願意資助的項目(高價值感知)
B)我沒有資助的項目,但不介意他們是否得到補貼(小價值感知)
C)我不想要補貼的項目(沒有/負價值)
目前,還沒有辦法區分B和C。也許UI可以允許用戶對某些項目投反對票(downvote),這些信息會影響補貼。其反對票只會影響沒有資助的項目之間的補貼分配。因此,否決所有其他項目就相當於否決零。而這源於這樣一個現實,即用戶不會為每一個能讓他們受益的項目提供資金。公共產品的本質是,它們中的許多人都喜歡給予小的、間接的好處,因此更容易識別那些明顯是欺詐性的或不可能以任何方式使之受益的項目。
給一些獨特貢獻者更高的權重
大多數攻擊通過貢獻大量的資源來利用執行超額影響的能力。這是因為在一個抗盜版的系統中,它比捐助者更容易積累資金。因此,降低“假”項目有效性的一個簡單方法是,為有更多貢獻者的項目提供更高的補貼。這限制了強烈偏好的影響,但值得權衡。
一個極端是,有CLR,它允許強烈的偏好,但很容易被共謀。另一個極端是,可以根據一個項目收到的獨特貢獻者的數量來劃分補貼。 Peter Watts的想法是用一個係數來選擇這個光譜上的最佳點。
結論
為解決在去中心化自治組織中最優公共產品供應的方法中存在的共謀問題,在Buterin(2019)提出了配對協調補貼的基礎上,Zoudavid提出了一種新的方法對這一具有豐富經濟意義的配對協調補貼進行了調整和改進,他提出了一種新的不協調係數的規範,並對配對邊界進行了調整,使得估計結果更加穩健。其與當前現有的方法相比,在對不協調進行調整之外,還對邊界進行了調整,使得補貼更為嚴格。該方法用點積來直接估計多個協調者之間的不相關關係,是一個突出亮點,但也同時存在潛在的應對發送至自身的供給的問題,以及真正的利益相關者得不到足夠補貼的問題。針對這一方法,還有很多值得探討和進一步深入挖掘的方向,包括“高階相關測度”和懲罰協調的機制等。
參考文獻
[1] Buterin、Vitalik、Zoë Hitzig 和 E. Glen Weyl,2018 年,“自由激進主義:慈善匹配基金的靈活設計”。 網址:https://papers.ssrn.com/sol3/papers.cfm?abstract_id=32436561
[2] Buterin, Vitalik, 2019b,“配對協調補貼:一種新的二次融資設計”。 URL:成對協調補貼:新的二次資助設計
原文作者: Zoudavid
討論者:Vitalik、Vbuterin、Peter Watts
貢獻者:演示,DAOctor @DAOrayaki
譯文: 改善成對協調補貼的建議