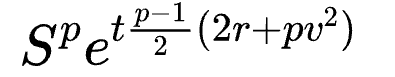Paradigm 近日設計了一種基於價格N 次方的新型永續合約。本文暫譯為乘方永續合約。整個DeFi 衍生品賽道還處於萌芽期，Paradigm 每次的設計和思考都站在前沿，值得學習。
原文標題：Power Perpetuals
作者：戴夫·懷特、丹·羅賓遜、祖賓·科蒂查、安德魯·萊昂、亞歷克西斯·高巴、阿帕納·克里希南
翻譯：路遙
簡介
本文介紹了一種新型的衍生品– 乘方永續合約（Power Perpetual）。
如果ETH 的價格翻倍，ETH 的2 次方永續合約翻4 倍，ETH 的3 次方永續合約翻8 倍，ETH 的5 次方永續合約翻32 倍。
當然，這種不對稱的上漲並不是免費的。那些做多乘方永續合約的人需要定期支付溢價收益，給那些做空的人。
乘方永續合約提供了類似於全球期權的風險敞口，而不需要行權價或到期日，使其有可能將大部分期權市場的流動性，整合到單一的工具中。
從不少方面來講，乘方永續合約都是永續期權合理的下一步。據我們所知，除我們外，研究人員Wayne Nilsen 和lllvvuu 也各自獨立發現了這種產品。
機制
前提條件
乘方永續合約是永續期權論文（鏈接見文末）中介紹的永續衍生品的一個特殊系列。
在本文接下來的內容中，我們將假設讀者已經熟悉永續期權和永續期貨的基本機制。
定義
乘方永續合約是指與某些標的資產價格的乘方掛鉤的永續衍生品。在本文中，我們將假設這個標的資產是以太幣。
對於任何乘方p，ETH^p 乘方永續合約都是通過定期（如每天）支付的資金費用來維持的。如果在註資時，乘方永續合約的當前價格是$MARK，做多乘方永續合約的人必須向做空的人支付$(MARK-INDEX) = $(MARK-ETH^p)。
在乘方永續合約裡，我們把這種資金費用稱為溢價收益(premium yield)。因為這種費用通常是由多頭向空頭支付的溢價，以換取類似期權的風險敞口。
例子
考慮ETH^2 乘方永續合約。
為簡單起見，假設ETH 的交易價格為$3，而在支付資金時，ETH^2 乘方永續合約的交易價格為$9.09。那麼每份合約多頭都將不得不向空頭支付$ (MARK-INDEX) = $(MARK-ETH^2) = $(9.09-3^2) = $9.09 – $9.00 = $0.09。
定價
概述
乘方大於1 的永續合約具有正的凸性，這意味著當價格對他們有利時，持有者賺錢更快，而當價格對他們不利時，虧錢則更慢。用期權的話說，我們說它們有正的伽馬值(gamma)。
就像期權通常以其內在價值的溢價交易一樣，ETH^p 的乘方永續合約通常以ETH 價格的p 次冪的溢價交易。
推導
按照永續期權論文中的方法，我們可以先對即將到期的乘方衍生品進行定價，然後這些衍生品的組合進行定價，這個組合剛好相當於所需的永續合約。
下面我們將使用Black-Scholes 假設來推導我們的價格。這些當然不是最合適的假設，但應該可以作為一個例子來說明做市商如何去給乘方永續合約估值。
在Black-Scholes 假設下給一個即將到期的乘方衍生品定價要比給期權定價簡單得多。有興趣的讀者可以在StackExchange 這裡找到一個快速推導。其價格為
其中S 是現貨價格，p 是乘方數，t 是到期時間，r 是漂移（drift）或者叫無風險利率，v 是年化波動率。
結合永續期權論文附錄B 中的永續期權定價方法，並對所得的幾何數列進行求和，我們可以得到每期支付一次資金的乘方永續合約的價格表達式如下（假設數列收斂– 見下文）：
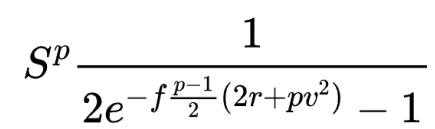
其中f 是以年為單位的注資期。
這可以解釋為指數S^p 乘以調整係數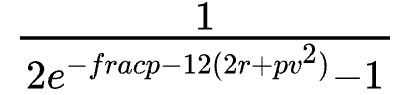
，該係數考慮了乘方永續合約的嵌入式期權性。需要注意的是，當注資期接近0 時，這個調整係數接近1。
溢價收益（我們對融資率的新術語）可以計算為：
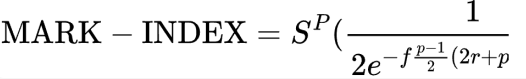
收斂性
我們總是可以對股票永續期權進行定價，而與之不同的是，配置不好的乘方永續合約可能會出現價格無法收斂的情況。特別是，我們只有在以下情況下才可以對乘方永續合約進行定價：
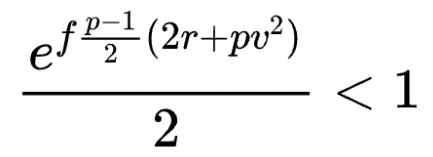
直觀地說，乘方數和波動率越高，長期的臨期乘方期貨就越有價值；注資期越長，乘方永續合約的價值就越集中於長期的乘方期貨。對某些組合來說，同等的投資組合可以變得無限有價值。
這個問題在實踐中可以通過選擇一個足夠小的注資期來輕鬆避免。
例子
ETH^2 乘方永續合約
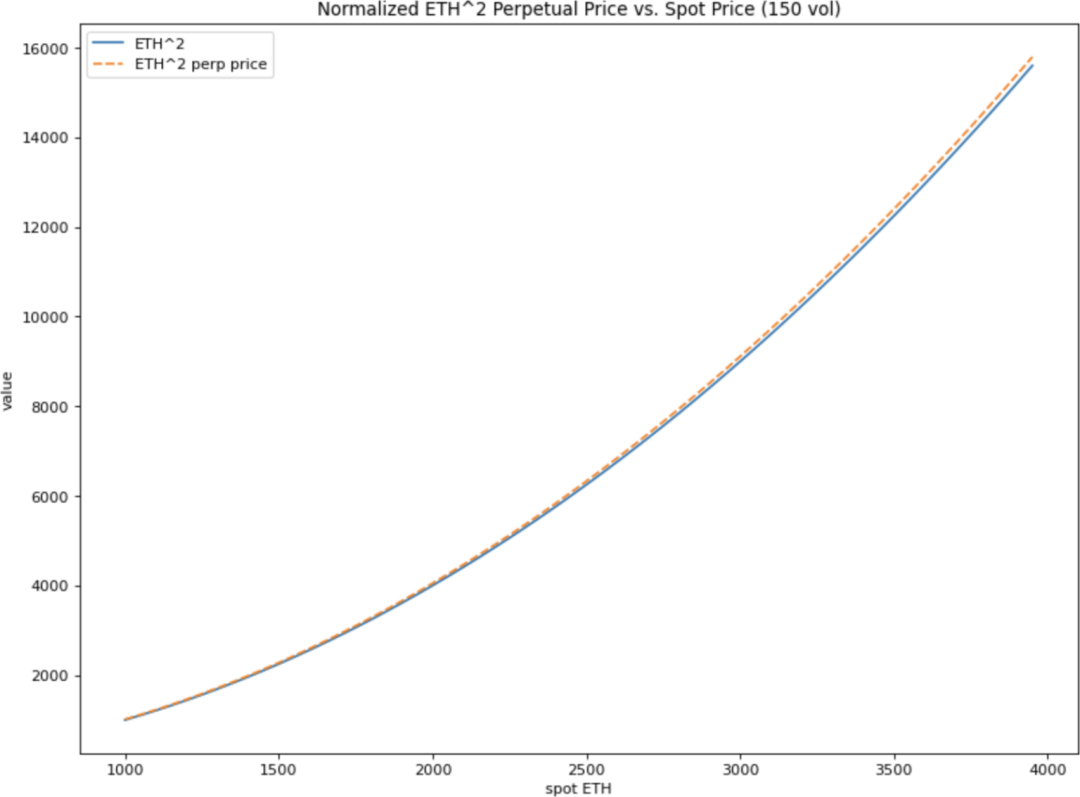
見 
https://github.com/para-dave/powerperps/blob/master/power_perp_prices.ipynb
在Black-Scholes 假設下，ETH^2 乘方永續合約的價格為
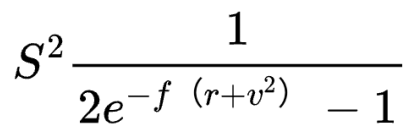
在其他條件相同的情況下，當ETH 價格4 倍時，它會翻16 倍。
它有一個很方便的特性，就是有一個恆定的伽馬值，即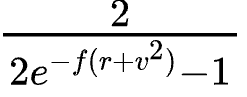
，這意味著無論ETH 的價格如何，它都能提供恆定的期權性。
我們親切地稱它為”squeeth”，是”ETH 平方” 的簡稱。
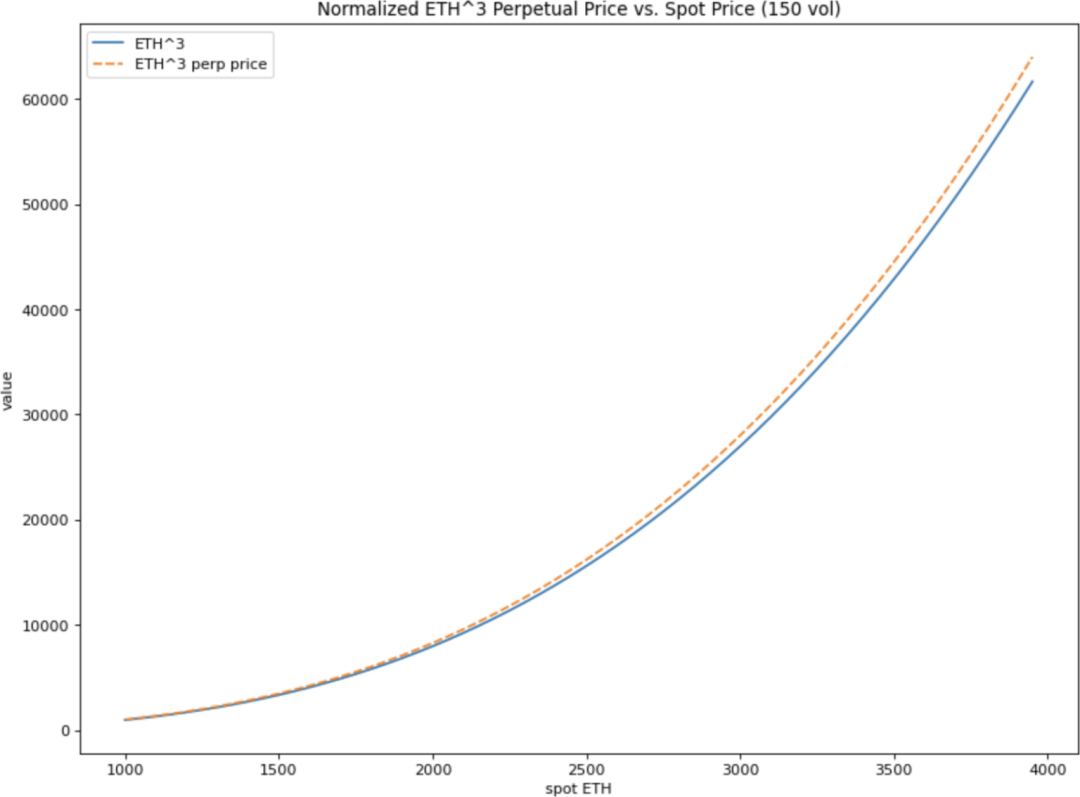
ETH^3 乘方永續合約
見 https://github.com/para-dave/powerperps/blob/master/power_perp_prices.ipynb
ETH^3 乘方永續合約的價格為
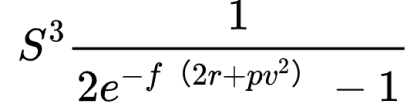
在其他條件相同的情況下，ETH 價格翻4 倍時，它將翻64 倍。
你可以從圖中清楚地看到永續合約的交易價格比其指數ETH^3 要高，因為它為持有者提供了期權。
Python 定價實現
你可以在 https://github.com/para-dave/powerperps/ 看到乘方永續合約定價的Python 實現，包括根據經驗證明正確性的測試。
總結
乘方永續合約仍處於起步階段，但我們從一開始就對其進行了深入的研究，並仍對其潛力感到非常興奮。
如果你和我們一樣對這種新東西感到好奇，我們很想听聽你的想法。你可以發郵件給dave@paradigm.xyz，或在Twitter 上給我發私信，或通過squeeth@opyn.co，聯繫Opyn。
鳴謝：lllvvuu、Wayne Nilsen、Wade Prospere、Grug、Lily Francus、Benn Eifert 博士、Jeff Wang、Mewny
鑑於微信無法給外鏈，文中有些外鏈在這裡給出：
-
永續期權論文
https://www.paradigm.xyz/2021/05/everstanding-options/ -
永續期權論文PDF
https://www.paradigm.xyz/papers/everlasting_options.pdf -
永續期貨
https://research.paradigm.xyz/cartoon-guide-to-perps -
StackExchange 上的價格推導
https://math.stackexchange.com/questions/1015926/derivatives-pricing-w-squared-and-cubed-stock-prices/3954177#3954177 -
Python 實現
https://github.com/para-dave/powerperps/
展開全文打開碳鏈價值APP 查看更多精彩資訊
