隱私比較是指在不暴露雙方具體數值的前提下,獲取雙方數值的大小關係。本文則主要介紹一種在當前效率比較高的隱私比較協議。
隱私比較是指在不暴露雙方具體數值的前提下,獲取雙方數值的大小關係。最早起源於姚期智的百萬富翁問題:有兩個百萬富翁想要比較下誰更富有,但是又不想透露自己有多少錢,如何在沒有可信第三方的情況下進行比較?這個問題是由中國第一個也是目前為止唯一一個圖靈獎獲得者姚期智在1980年代提出的,他是中國計算機學術和教育的第一人,為現代密碼學打開了一道新的大門。
在之前的文章《優雅的求職——隱私比較算法實例》中已經通過求職案例介紹了隱私比較的應用場景以及如何實現,本文則主要介紹一種在當前效率比較高的隱私比較協議。
該協議是[1] CrypTFlow2: Practical 2-Party SecureInference中提出的一個子協議,並基於此協議實現DRelu激活函數應用於神經網絡中。
–相關技術–
該協議主要使用了布爾秘密分享和不經意傳輸兩種技術進行構建:
▲ 不經意傳輸
不經意傳輸(OT,Oblivious Transfer)是指數據發送方有n個數據,數據接收方接收其中的一個數據,且數據接收方不能獲取其他的數據,數據發送方也不知道接收方選擇接收的數據具體是哪一個。在之前的文章《基於安全多方計算(MPC)的隱私計算技術(一)》中已介紹過一種實現方案,故本文不再贅述。
▲ 布爾秘密分享
在安全多方計算中會使用秘密分享將數據進行拆分後分享出去,每一方拿到每個數據的相應碎片,對於原始數據的計算邏輯都會轉為對碎片的計算,在整個計算邏輯完成後,再將碎片的計算結果進行匯聚還原以獲取原始數據的計算結果。
布爾秘密分享是指將一個布爾值b拆分成兩個碎片b0、b1,將兩個碎片匯聚到一起即可還原出原始數據b。
碎片生成:隨機生成一個布爾值b0,並和b執行異或計算出b1=b0⊕b
碎片還原:對兩個碎片執行異或操作
b=b0⊕b1
異或運算:布爾秘密分享在異或操作上是滿足同態性質的,在本地通過對碎片進行異或操作再還原就等價於對原始數據的異或操作
a=a0⊕a1,b=b0⊕b1
a⊕b=(a0⊕b0)⊕(a1⊕b1)
與運算:布爾秘密分享對於與操作不滿足同態性質,使用不經意傳輸技術以實現安全的與操作:
Alice持有碎片a0和b0,Bob持有碎片a1和b1,通過與運算使得Alice獲取c0,Bob獲取c1,c0⊕c1=(a0⊕a1)∧(b0⊕b1),並保證雙方碎片的安全;
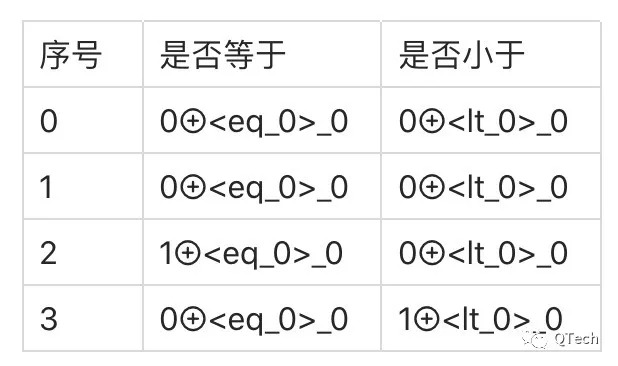
Alice作為不經意傳輸的發送方,隨機生成一個布爾值r作為c0,並按下圖生成不經意傳輸的輸入:
圖片
Bob作為不經意傳輸的接收方將自己的碎片a1,b1拼接成a1||b1作為不經意傳輸的選擇項獲取數據r⊕((a0⊕a1)∧(b0⊕b1))作為c1;
可驗證c0⊕c1= r⊕r⊕((a0⊕a1)∧(b0⊕b1))=(a0⊕a1)∧(b0⊕b1);
本質是將與運算的所有可能性羅列出來,加入隨機項後由另一方根據自己的數據選擇混淆後的計算結果。
–實現思路–
▲ 明文比較
首先不考慮比較運算的隱私性,平常情況下兩個數是如何比較大小的:
將兩個數對齊為相同長度的數字數組,長度不夠的則在前面補0
a=123,b=5879,a=>[0,1,2,3],b=>[5,8,7,9]
對兩個數組裡面的數字進行順序比較,如果對應位的數字相等,則繼續比較下一位,直到有一位不相等,最早不相等那位的比較結果即為兩個數據的比較結果,若所有位的數字都相等,則兩個數據相等。整個過程可歸納為以下公式:
X,Y都是長度為n的數據,1{X X=x0||x1||x2||…||x(n-1),Y=y0||y1||y2||…||y(n-1),xi,yi表示拆分後的第i位數據 Xi=xi||…||x(n-1),Yi=yi||…||y(n-1),用於表示去除前i-1位後的數據 1{X 1{X1 … 1{X(n-1) ▲ 不安全的隱私比較 如果要將上述比較方案轉為隱私比較,最容易想到的方案是將兩個最小比較單位的數的比較隱私化,在之前的文章《優雅的求職——隱私比較算法實例》中已經介紹過:對於兩個最小比較單位的比較可通過不經意傳輸協議來完成。這樣確實是保證了單個最小比較單位的安全性,但是對於某些情況,會暴露出數據的一些情況: a=1230 b=1231,對於這兩個數字的比較,如果b作為ot的接受方也就是最小比較單元數據比較結果的獲取方,按照上述方案進行比較,會有兩點額外信息被洩露: 1)在前幾位相同的情況下:b會知道a的前三位是123; 2)兩個最小單元的數據是最小單元範圍的兩端數據:b會知道a的最後一位是0; 而根據以上兩個信息b甚至可以直接反推出a的數據,在這種情況隱私比較也就不隱私了。 本論文中的隱私比較協議,整個比較思路和上面不安全的隱私比較是一致的,但是該協議引入了秘密分享技術,在通過不經意傳輸協議獲取比較結果時發送方對每個數據都混淆上一個隨機項,這樣雙方都不會獲取到最小比較單元數據的比較結果,而是比較結果的碎片,並使用碎片按照明文比較的流程遞歸的進行比較,所有最小比較單元都比較完成後,再將比較結果的碎片進行還原以獲取整個數據的比較結果。 由於最小單元的比較結果都是碎片,到比較結束才會還原遞歸計算的結果,就避免了獲取最小比較單元比較結果導致的信息洩露。 –協議流程– Alice擁有數據x,Bob擁有數據y,數據的二進制長度為l,最小比較單元的二進制長度為m,劃分的最小比較單元個數為q=l/m,最小比較單元的十進制最大值為M=2^m-1 1)雙方分別劃分數據:x=x0||…||x(q-1),y=y0||…||y(q-1) 2)對於所有的最小比較單元xi(0<=i Alice作為不經意傳輸的發送方准備數據:隨機生成布爾值 sij= tij= Bob將yi作為輸入分別執行兩個不經意傳輸實例,獲取兩個比較結果的碎片: 例如當m取2時,Alice的第一個最小比較單元x0=2,Bob的第一個最小比較單元y0=1,Alice隨機生成 Bob使用y0作為兩個不經意傳輸的選擇項,獲取: 3)所有最小比較單元比較完成後,雙方都獲取了對應的最小比較單元間是否小於和是否等於的布爾分享碎片,即可按照明文比較流程,使用碎片遞推計算出最終比較結果的碎片。 對於碎片的異或操作,只需要進行本地對碎片進行異或就行。對於碎片的與操作,則需要按照上面介紹的方案通過不經意傳輸計算出結果的碎片。 在遞推過程中主要有兩個地方需要執行與操作: 當前面所有比較單元相等,需要比較下一個時: 1{x0||x1 = y0||y1 } ∧ 1{x2 < y2 } 計算前面所有比較單元是否都相等時: 1{x0||x1 = y0||y1} = 1{x0 = y0 } ∧ 1{x1 = y1 } –總結– 該協議整體思路和明文的比較流程一致,並使用不經意傳輸和秘密分享技術保證數據的隱私性,也是當前效率比較高的協議。 對於單個元素的比較,與運算的OT實例,無法通過OT擴展進行優化,因為需要進行遞歸的計算,前後有依賴關係。對於批量元素的比較則可在縱向對於相同位置與運算的OT實例通過OT擴展來優化效率。 作者簡介 劉敬趣鏈科技數據網格實驗室BitXMesh團隊 參考文獻 原論文:Rathee D, Rathee M, Kumar N, et al. CrypTFlow2: Practical 2-party secure inference[C]//2020 年 ACM SIGSAC 計算機和通信安全會議論文集。 2020 年:325-342。 展開全文打開碳鏈價值APP 查看更多精彩資訊▲ 消除不安全
 圖片
圖片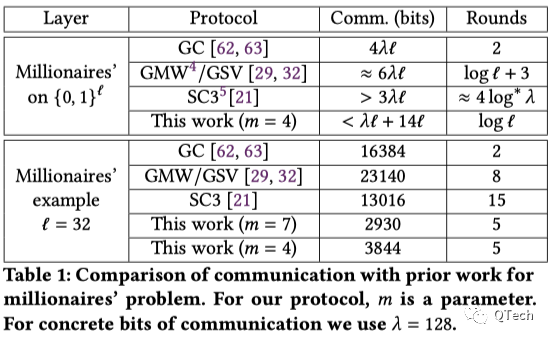 圖片
圖片

