在本文中,我們將首先回顧由Bancor、Uniswap、Balancer 和Curve 協議實現的四種自動做市商(AMM) 算法。還將討論AMM 算法的最新發展、可能的改進和未來。
本文總共分為上、中、下篇闡述自動做市商算法、現狀及未來迭代的思考,本文為上篇。
目錄
-
Bancor Network的聯合曲線概念和交易公式
-
Uniswap 的無常損失計算
-
當價格變動在2ρ之間時的正向收益
-
流動性分佈、流動性注入、Uniswap V3 範圍訂單
-
Balancer 的做市函數和交易公式
-
智能訂單路由(SOR)算法
……
Bancor Network 的聯合曲線概念和交易公式:
Bancor¹利用聯合曲線的概念來確定價格。聯合曲線是代幣價格與其總供應量之間的關係。
班科¹
Bancor 協議通過其智能合約為加密代幣提供持續流動性
https://storage.googleapis.com/website-bancor/2018/04/01ba8253-bancor_protocol_whitepaper_en.pdf
聯合曲線Bonding Curve:
聯合曲線模型可以理解為描述“代幣買賣價格”與“代幣發行總量”之間的函數關係,可以由智能合約以去中心化的方式自動執行。
https://medium.com/linum-labs/intro-to-bonding-curves-and-shapes-bf326bc4e11a
Bancor Network選擇的不變量是F,稱為連接權重。在第一個表達式中R是指流動性池中的儲備代幣數量,S是流動性池外的BNT總供應量,P是BNT和儲備代幣的相對價格。我們可以代入P的方程,對兩邊積分²得到P和S之間的關係。這是一個指數表達式,其中指數α與連接權重F有關(F在0和1之間)。 F越小,α越大,這意味著價格相對於BNT的總供應量變化得更快。
兩邊積分²
Bancor 系統的公式
https://drive.google.com/file/d/0B3HPNP-GDn7aRkVaV3dkVl9NS2M/view?resourcekey=0-mbIgrdd0B9H8dPNRaeB_TA
使用這個表達式和簡單的積分,我們可以導出T(購買的BNT代幣)和E(支付的儲備代幣)之間的關係,其中R0,S0是R和S的當前值。
如果我們想在代幣A和代幣B之間交換,則將代幣A出售給代幣B。我們首先需要使用代幣A從池A購買BNT代幣(注:如果我們沒有BNT代幣)。接下來,我們需要使用BNT從池B購買代幣B。下面是計算我們將收到多少代幣所需的精確公式。代幣A和代幣B之間的相對價格可以用BNT代幣和代幣A/B之間的相對價格表示。

優點:Bancor 允許在某些池中進行單邊流動性的注入,這由Bancor治理決定。可以存入多少單邊流動性是有限制的,這也是由Bancor治理決定的。在限額內,當用戶以其他代幣的形式存入單邊流動性時,Bancor將補充等值的BNT 代幣。這使得用戶提供的有效流動性加倍。如果達到限額,如果人們想要存單邊流動性,就得等有人提取單邊流動性,或者有人把BNT做為單邊流動性注入。
Bancor 協議以BNT部分賺取的手續費補償用戶在存入單邊流動性時的無常損失(將在後面討論)。如果交易費用不能完全補償無常損失,Bancor將鑄造BNT以確保無常損失為零。因此,流動性提供者如果將流動性存入一定的時間(存入滿100天可全額補償),就可以享受穩定的收入。
缺點:如上所述,所有交易都需要BNT 代幣作為中介。因此,我們將經歷兩次滑點。由於相同的原因,所有流動性池都由BNT 和另一個代幣組成,因此缺乏多樣性。 BNT 代幣價格也可能受到影響,因為需要彈性供應才能實現無常損失補償和單邊流動性存款。
Bancor 引入了連接代幣BNT 的概念,它連接到所有具有不同連接權重的代幣,對應不同決定價格的聯合曲線。
Uniswap 的無常損失計算:
Uniswap 使用恆定乘積做市商(CPMM) 來決定價格。在我們深入研究Uniswap V2 和V3 使用的算法之前,讓我們先了解什麼是無常損失(IL) 以及如何計算它。
恆定乘積做市商(CPMM)
恆定產品做市商
強制要求兩種資產儲備量的乘積必須始終保持不變x*y=k
https://ethresear.ch/t/improving-front-running-resistance-of-xyk-market-makers/1281
無常損失
無常損失
是指資金在流動性池中面臨的損失。
https://finematics.com/impermanent-loss-explained/

如果AMM 函數是凸的(注:價格隨著我們買入而增加/ 價格隨著我們賣出而減少),那麼沒有交易費用補償的單筆交易總是會導致流動性提供者賠錢。假設一筆交易導致AMM 函數從點1 移動到點2。點1 和點2 的現貨價格(函數導數的絕對值)是P1 和P2。 P3 為實際交易價格。由於凸函數的性質,P1 > P3 > P2。無常損失定義為交易後池中流動性提供者代幣的當前價值與流動性提供者的代幣當前價值之間的差值,如果他只是持有他的代幣而不將它們用於流動性提供,則表示為V 和Vheld。為方便起見,無常損失和價格將以代幣Y 表示(1 個代幣Y 的價格為單位1)。經過一些簡單的推導,很容易證明無常損失總是小於零(x2 > x1,P2 < P3)。
Uniswap³ V2 使用一個簡單但功能強大的公式來確定交易。池代幣儲備數量的乘積是一個常數。與Bancor 相比,它擺脫了連接代幣的依賴。交易完全由流動性池中的代幣數量決定。
Uniswap³
Uniswap V2 核心
https://uniswap.org/whitepaper.pdf

由於此函數的性質,池中兩個代幣的價值將始終相同(我們在本文中使用的價格將始終是相對價格)。
使用相同的邏輯,不難計算Uniswap V2中單筆無手續費的無常損失。假設交易將價格從P更改為Pk。以百分比衡量的無常損失可以單獨表示為k的函數。

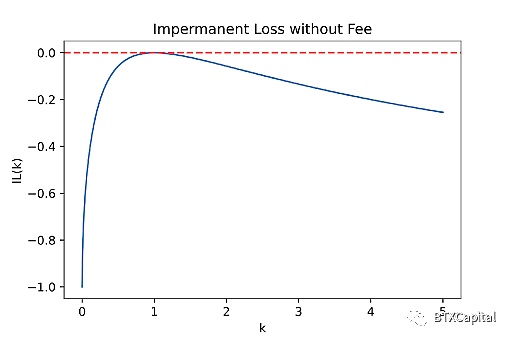
毫不奇怪,這個函數總是小於或等於零,正如我們從上面沒有費用的無常損失圖中可以看出的。如果在對數空間中繪製橫軸,則IL(k) 將是對稱的。結論是:相對價格變化越大,無常損失就越大。這可以解釋為流動性提供者的更有價值的代幣從池中被買出,留給他們更多價值較低的代幣。
當價格變動在2ρ之間時的正向收益:
接下來,讓我們看看如果我們添加交易費用,IL(k) 會如何表現:

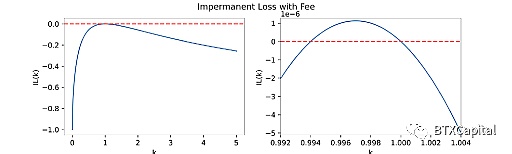
導出的無常損失函數IL(k, ρ) 看起來與無費用的無常損失函數非常相似。我們可以通過將ρ設置為零來進行合理性驗證,得出相同的結果。典型的Uniswap V2 費用百分比為ρ= 0.3%。在繪製無常損失函數時,我們可以看到在大約k= 0.994 到1(大約2ρ跨度)之間有一個高於零的部分。在該地區,無常損失是正的,這意味著流動性提供者實際上獲得了價值(在該地區賺取的交易費用優於損失)。通過引入交易費,當價格在一定範圍內波動時,流動性提供者將獲得正收益。
當價格變動更加波動時,流動性提供者似乎總是會出現虧損。然而,實際情況並非如此。我們知道Dave White4(注:Paradim風險投資基金研究員)等人解決了這個難題。遺憾的是,它超出了這篇介紹性論文的範圍。我們打算在未來進一步研究這個問題。
戴夫懷特4
Uniswap 的金融煉金術
https://research.paradigm.xyz/uniswaps-alchemy
至於其他流行的AMM 算法(包括Uniswap V3)的無常損失推導,我們向讀者推薦Jiahua Xu⁵等人的這篇論文。這些推導將是下一次的主題。
Jiahua Xu⁵
SoK:具有自動做市商 (AMM) 協議的去中心化交易所 (DEX)
https://arxiv.org/abs/2103.12732
優點:第一個用池中代幣數量的凸函數來確定價格。
缺點:流動性供應均勻分佈於所有價格範圍,這意味著資本效率較低。
流動性分佈、流動性注入、Uniswap V3 範圍訂單:
為了提高流動性效用並降低無常損失風險,Uniswap⁶ V3 允許用戶僅在特定價格範圍內提供流動性。
Uniswap⁶
Uniswap V3 核心
https://uniswap.org/whitepaper-v3.pdf
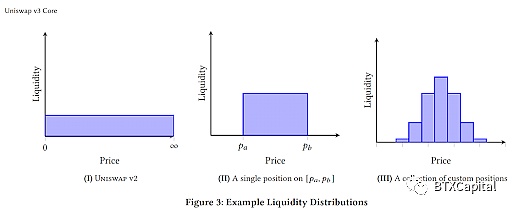
來自 Uniswap V3 白皮書
這是通過對Uniswap V2 函數進行平移來實現的:
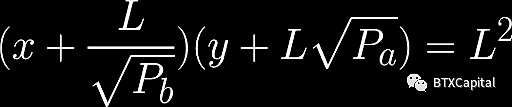
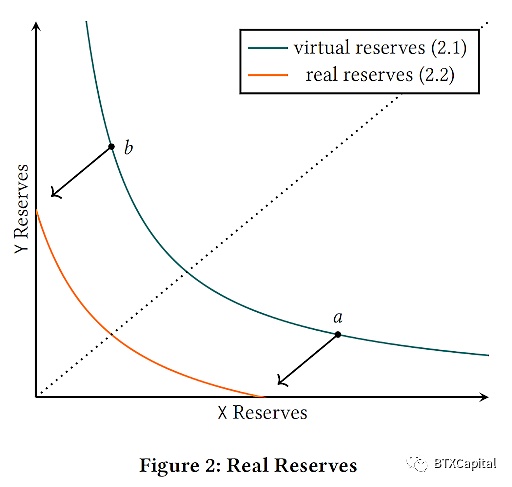
來自 Uniswap V3 白皮書
將函數向下平移a點的y值,向左平移b點的x值,如上圖和等式所示,確保a 和b之間的有效交易結果,就像我們使用綠色曲線作為我們的價格決定函數。當價格超出此範圍時,其中一個代幣儲備將被售罄,從而有效地將流動性集中到此價格範圍內。
Dan Robinson⁷ (注:Paradim風險投資基金研究員主管)發表了一篇關於計算多個AMM 的流動性分佈的優秀論文。
丹·羅賓遜⁷
Uniswap V3:通用 AMM
https://www.paradigm.xyz/2021/06/uniswap-v3-the-universal-amm/

也可以簡單地證明,兩個流動性提供者在同一價格範圍內的流動性可以簡單地加在一起。
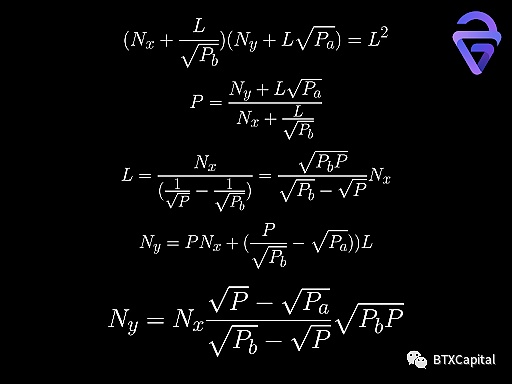
在存入流動性時,如上所示,Uniswap V3中每個資產的價值不一定相等。只有當P等於Pa和Pb 的幾何平均值時,每個資產的價值才相等。當P小於幾何平均值時,資產X的價值大於資產Y的價值。當P大於幾何平均值時,資產X的價值小於資產Y的價值。
噹噹前價格完全超出流動性提供者設定的價格區間時,Uniswap V3將流動性提供者的輸入算作範圍訂單(Range Order),只允許其存入一種代幣(類型取決於價格區間是否完全高於或低於當前價格)。例如,考慮一個由ETH 和Dai 組成的流動性池。如果設定的價格區間完全高於ETH 的當前價格,則只允許用戶存入ETH。如果價格區間完全低於ETH 的當前價格,則只允許用戶存入Dai。當價格完全越過流動性提供者設定的價格區間時,他存入的資產將全部轉換為另一種的代幣。由於用戶只能存入一種代幣,範圍訂單只能實現傳統限價訂單中四分之二的訂單(獲利訂單、買入限價訂單)。另一方面,買入止損訂單和止損訂單無法實現。截至目前,我們不知道限制範圍訂單代幣類型的目的是什麼。
範圍訂單
範圍訂單
本質上並不是真正的訂單,而是LP 向資金池某個特定價格點提供的聚合流動性。雖然不是真正的訂單,但「範圍訂單」所表現出的特性,卻很好地模擬了限價單的基本功能。
https://docs.uniswap.org/protocol/concepts/V3-overview/range-orders
優點:Uniswap V3 引入了流動性分佈的概念,允許其用戶在價格範圍內存入流動性。通過集中流動性,提高資本效率。當存入相同價值的資產時,可以獲得更高的流動性和更低的滑點。在某個價格範圍內提供流動性也在某種程度上降低了無常損失的風險。
缺點:用戶在進行範圍訂單時只能存入某些類型的代幣。因此無法實現買入止損訂單和止損訂單。
Uniswap V2 和V3 在其AMM 算法中引入了CPMM 和流動性分佈。提供價格範圍內的流動性本質上使Uniswap V3 成為一個通用的AMM,能夠通過改變其流動性分佈成為任何可能的AMM。
Balancer 的做市函數和交易公式:
Balancer⁸ 將Uniswap V2 的雙代幣池擴展到多代幣池。 Balancer 池中每種資產的價值都持有一個不變的權重,加起來為1。不難證明,這相當於每種資產的儲備數量的冪乘積是一個常數。資產n 相對於資產t 的價格也可以導出為資產t 和n 的儲備數量之間的比率,通過它們的權重進行歸一化。
平衡器⁸
非託管投資組合經理、流動性提供者和價格傳感器
https://balancer.fi/whitepaper.pdf

基於常數不變式,我們可以求導出有不同輸入值的交易公式(資產o 和資產i 之間的交易)。在這種記法標準中,資產o 始終是買出的資產。資產i 是賣出的資產。 A 和B 是打入/接收的代幣和當前的代幣儲備數量。我們還可以根據價格的變化計算打入的代幣或買出的代幣數量。
智能訂單路由(SOR)算法:
Balancer 還引入了智能訂單路由(SOR⁹) 算法。
SOR⁹
智能點餐路由器 V2
https://docs.balancer.fi/developers/smart-order-router
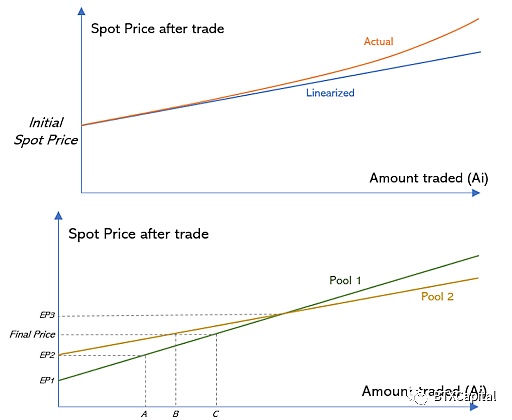
來源:https://docs.balancer.fi/v/v1/smart-contracts/sor/
該算法的總體思路是將一個訂單分成幾個小塊在不同的Balancer池中進行交易,以獲得更好的交易結果。假設我們要在代幣池1和代幣池2進行交易,如果我們要交易的總金額N低於上圖中的A,我們將只在代幣池1進行交易,因為代幣池1的價格總是比代幣池2價格好。如果總金額超過A,我們將部分訂單在代幣池1中交易,部分在代幣池2中交易。在每個代幣池中交易的數量將使每個池中的價格相等(B + C = N)。
很容易證明最優策略總是使每個池中的價格相等的策略(如果價格不相等,我們總是可以找到一個價格更好的池來改善我們的交易結果)。
價格函數,相對於交易量,通常是一個非線性函數。 Balancer 將價格函數簡化為線性函數。如果有n個代幣池,最優策略可以表示為:

如果存在一個價格函數總是大於或小於範圍(0, N) 的其餘價格函數,則應從上述計算中刪除該價格函數和相應的池,以確保結果有效。如果價格函數總是較小,那麼顯然的最佳策略將是在該池中交換所有代幣。
在這個計算中,不用考慮gas費用。實際上,最優策略應該是在路由收益和gas費用損失之間保持平衡。
SOR 算法,我們相信可以在更廣泛的背景下使用。例如,價格函數可以是其他AMM 協議池的函數。由於我們目前知識的限制,我們不確定實際的AMM 聚合器是否使用相同的邏輯來實現更好的價格。沒有任何價格函數近似的更通用的解決方案將在本文後面討論。
優點:Balancer 將2 個代幣池推廣到多個代幣池,並引入SOR 算法為其用戶實現更好的價格。
缺點:“流動性池的強度取決於其最弱的資產。” 一個池中的代幣類型越多,風險就越高。
Balancer 是一種多代幣投資組合管理工具,允許靈活的代幣價值分配,具有價格優化算法。
由於本論文過長,Curve的討論及後續內容將於中篇和下篇公佈。
原文鏈接:https://link.medium.com/ynEydZUihjb