撰文：Mellow Protocol
編譯：Blake
大家好，客套話就不說了，讓我們談談Uniswap V3 的數學邏輯吧！
我們將深入探討Uniswap V3 中流動性供應的工作原理，以及如何調整兩種代幣的投資組合，以便您產生最大的LP 頭寸，同時將IL 降至最低。接下來會有很多的公式和數字。
Uniswap V2 回顧：交易者的角度
Uniswap V2 是一個自動化的做市商，它允許：
- 交易者將一種資產換成另一種資產；
- 流動性提供者(LP) 提供流動性並賺取交易費用。
每個池有兩種代幣：X 和Y。如果池內有Xp 個X 代幣和Yp 的Y 代幣（也稱為池儲備），則池流動性L 定義為：
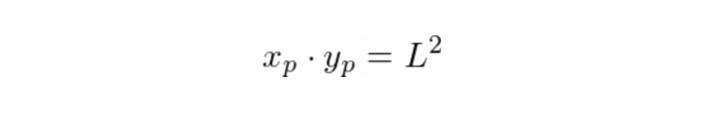
當前池中代幣的比例定義了當前的交換價格p：
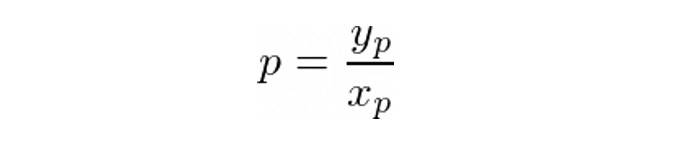
如果交易者想要交換y 個Y 代幣，他們將y 個代幣存入池中並收到x 個X 代幣。 x 由池使用以下等式決定：
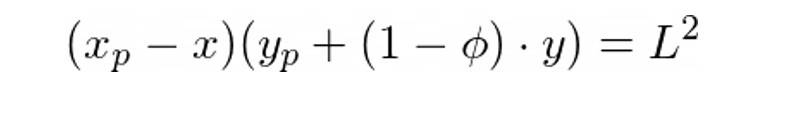
這裡的ϕ是池費。對於Uni V2 來說，它的數值是0.3%。
現在假設當ϕ= 0 時，讓我們看看如果當前價格p = 1，池儲備Xp=1，Yp=1，並且交易者想要交換y= 1 個單位的Y 代幣會發生什麼。
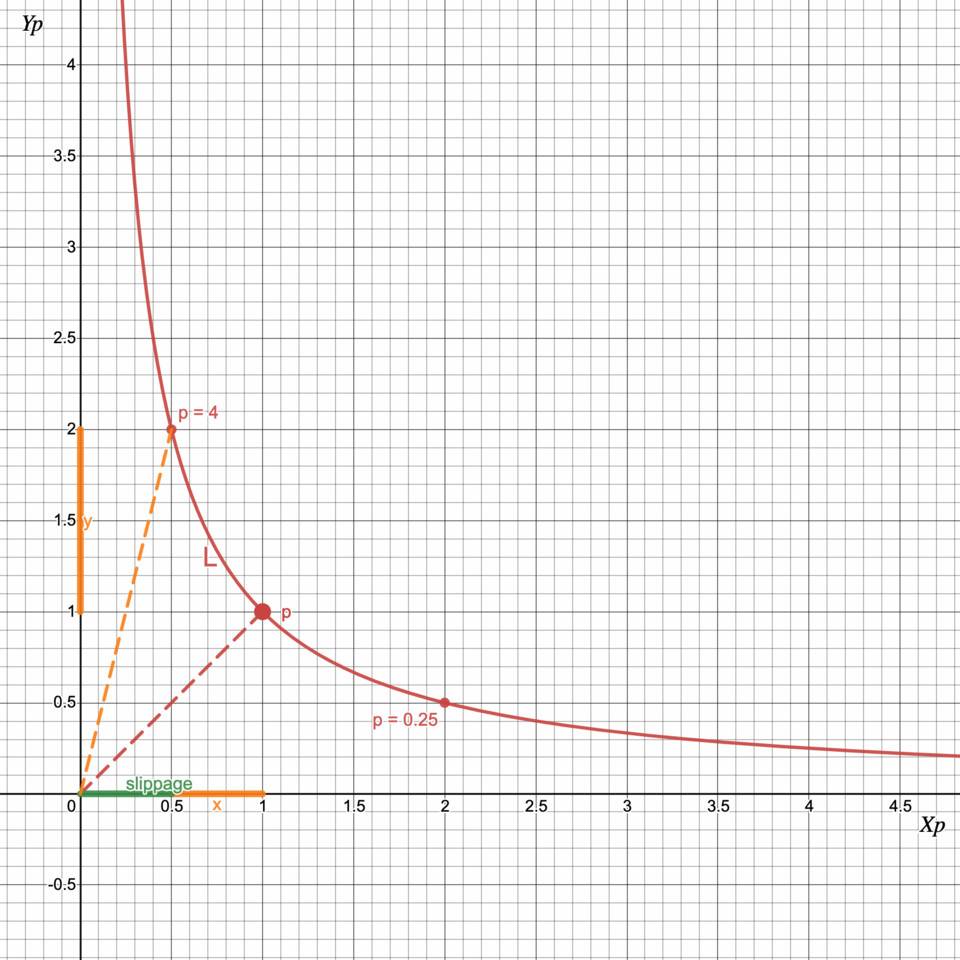
圖1：Uniswap V2 交易者的角度
交易者將收回X 的x = 0.5 代幣。池儲備和價格將更新為Xp = 0.5, Yp = 2, p = 4。
我們預計當前價格p = 1 時x = 1，但實際x 金額會受到損失，我們稱之為滑點（sl= 0.5）：
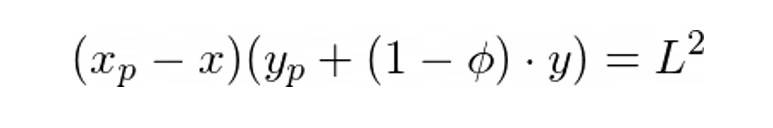
好消息是sl→0，因為池流動性L 增加或交換量減少，即對於足夠小的交換量，您以價格p 交換的費用較小。
Uniswap V2 回顧：流動性提供者的角度
現在讓我們看看如果p = 4，池準備金Xp = 0.5，Yp = 2，L = 1 並且流動性提供者想要放置x = 0.25 的代幣X 和y = 1 的代幣Y 會發生什麼。
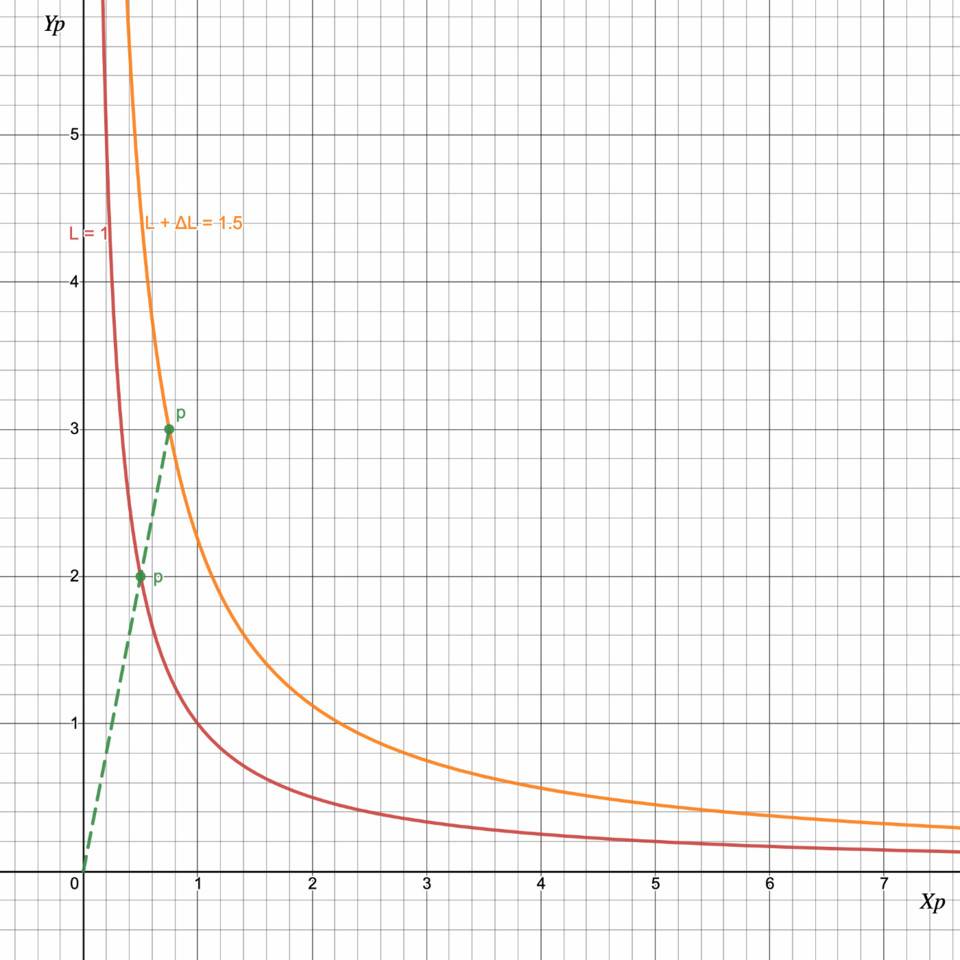
圖2：Uniswap V2 流動性提供者的角度
在這種情況下，池的新儲備將為Xp = 0.75、Yp = 3 和L² = Xp·Yp = 2.25，因此L = 1.5 並且流動性提供者以Uni V2 lp 代幣的形式收到ΔL = 0.5 的流動性。現在，在每筆交易中，流動性提供者將收到ΔL/L=1/3 份額的費用。
在這個例子中，我們故意使用x = 0.25 和y = 1 作為流動性提供者的投資，因此y / x = 4 = p。
如果y / x≠p 會發生什麼？在這種情況下，一部分代幣Δx 或Δy 會被返還給流動性提供者，使得剩餘比率(y-Δy)/ x = p 或y / (x-Δx) = p。如果流動性提供者想要充分利用他們的代幣並獲得最大的流動性，他們首先必須交易他們的代幣，以便y / x = p 然後將它們放入池中。
對於Uni V2，調整您的代幣組合以獲得最大流動性非常簡單。 Uni V3 會怎麼樣呢？事實證明這越來越複雜。
Uniswap V3：單倉
2021 年5 月，Uniswap 團隊推出了V3。在Uni V3 上，您可以將流動性置於任何價格區間 [pᵃ, pᵇ]。只要價格在 [pᵃ, pᵇ] 範圍內，您就有流動性L 並賺取費用。當價格超出範圍時，您不會賺取任何費用，直到價格回到範圍內。
讓我們看看它是如何運作的。首先，讓我們考慮只有一個持倉且價格區間為 [pᵃ, pᵇ] = [0.25, 4] 的礦池。當前池準備金為Xp = Yp = 0.5，價格為p = 1。在這種情況下，隨著交換發生且價格在變動，我們觀察到以下池行為：
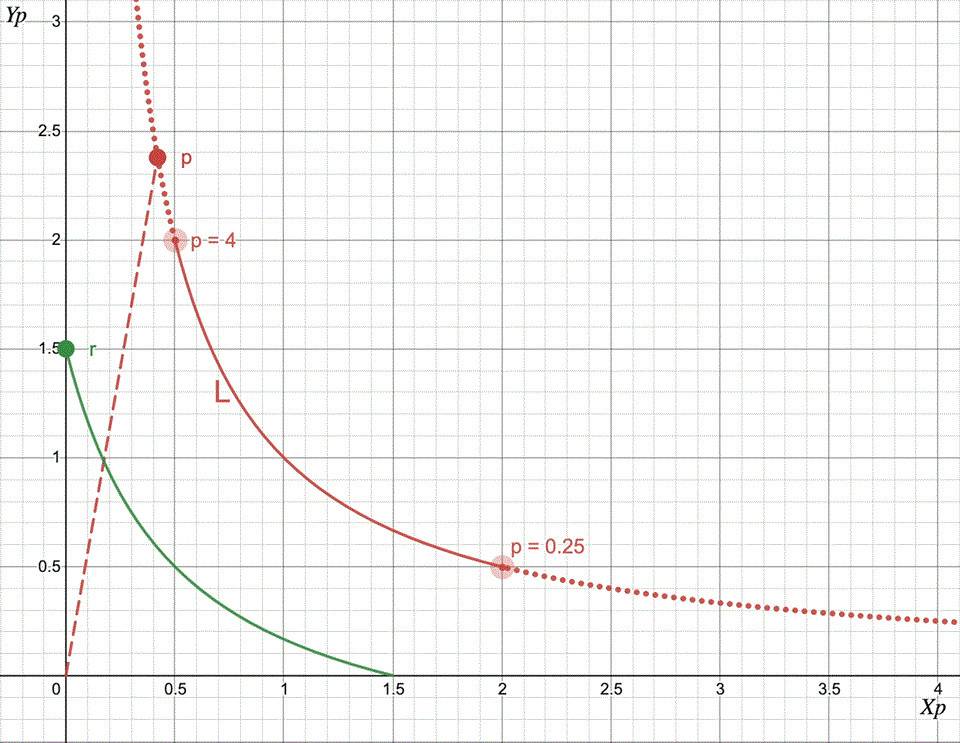
圖3：Uniswap V3 單倉
這裡綠色曲線是用於交換的實際代幣儲備（真實流動性曲線），紅色曲線是虛擬流動性曲線，模擬用戶在Uni V2 上進行交換。
只要價格在 [0.25, 4] 範圍內，池的行為就與擁有紅色流動性曲線的UniV2 池完全相同。當價格越界時，虛擬流動性降至零，實際流動性集中在X 或Y 代幣中，不用於交換。
Uniswap V3：多倉
現在讓我們看看如果在 [pᵃ₁, pᵇ₁] 上有兩個流動性投資x₁, y₁和在 [pᵃ₂, pᵇ₂] 上有x₂, y₂會發生什麼。這些投資中的每一個都意味著（我們將在後面的章節中看到）虛擬流動性L₁和L₂
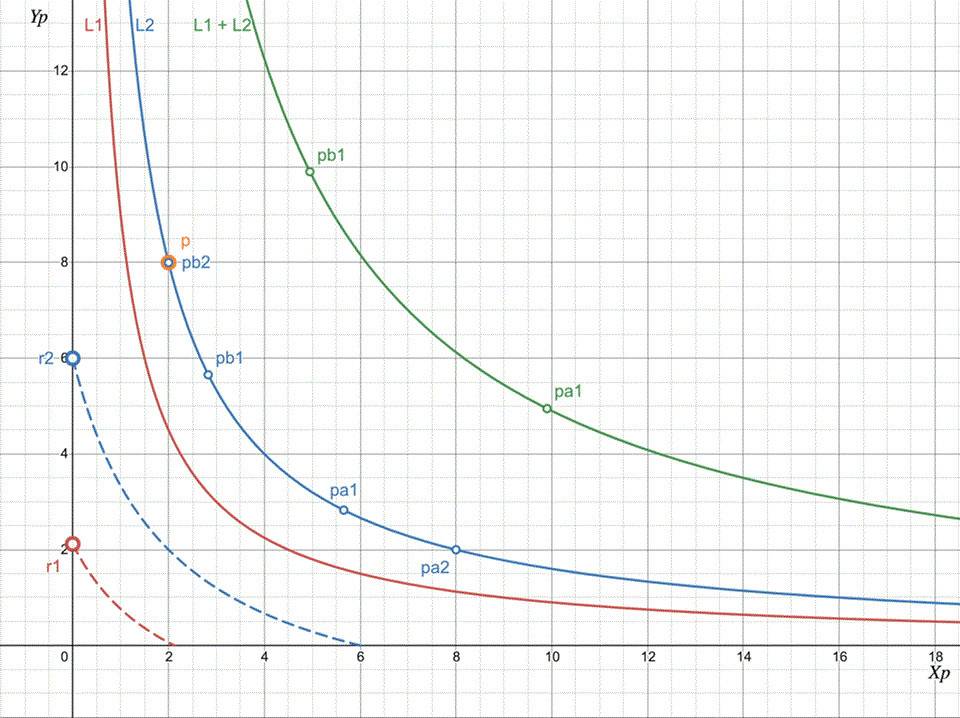
圖4：Uniswap V3 兩個倉位
可以看出，當兩個區間都覆蓋價格時，兩個實際儲備都被使用，池虛擬流動性等於流動性總和。當只有一個區間覆蓋價格時——僅使用其流動性。當價格在兩個區間之外時，池流動性為零（或者您不賺取任何費用）。
這為Uni V3 提供了一個獨特的特點——分段流動性函數。當價格沿著虛擬曲線移動時，流動性價值在某些價格點（即流動性頭寸的邊界）上變化了一些ΔL。您可以在圖3 中看到在價格pᵃ₁ 和pᵇ₁ 處發生這種跳躍。
刻度和刻度間距
Uniswap V3 的實際情況比上圖中顯示的要困難一些。在真正的Uni V3 中，您不能將流動性置於任意價格區間。取而代之的是，所謂的刻度在價格範圍內形成了一個離散的網格。刻度由公式定義（i 是整數）：
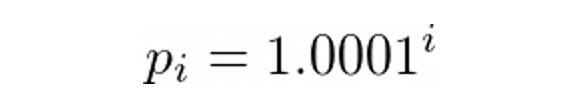
對於每個池，還有一個刻度間隔的概念。刻度間距是刻度之上的另一個網格，它限制了您可以放置流動性的刻度。例如，對於0.3%-費用的池刻度間隔是60，這樣你可以只在每個60 的刻度上放置流動性，例如，0, -60, 60, 120, -120, … 下圖顯示了刻度間距刻度（橙色）和刻度（黑色）
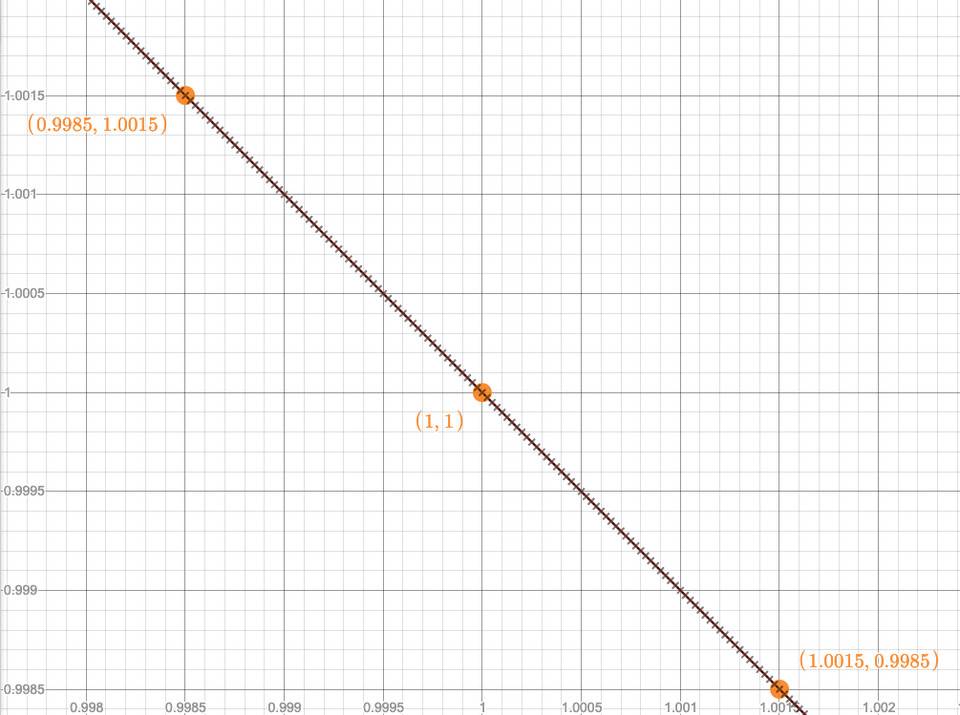
圖5：刻度和刻度間距
因為您的流動性價格區間界限只能是刻度間距刻度，所以任何空間刻度間隔內的流動性都是恆定的，並且只有在價格穿過刻度間距刻度時才會改變。
因此，我們有一個分段流動性函數，其中可能在刻度間隔刻度處發生跳躍（類似於圖2）。
倉位的流動性價值
讓我們看看流動性L 是如何計算的，給定初始代幣x 和y、價格區間 [pᵃ, pᵇ] 和當前價格p。
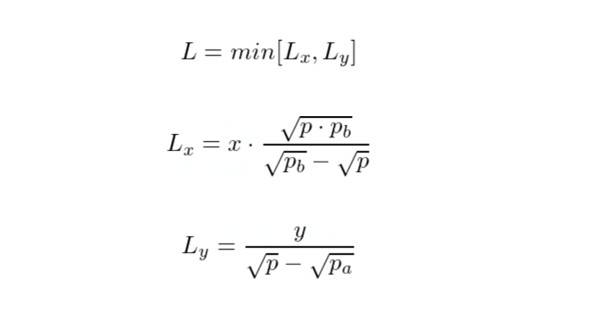
從這些等式中可以看出，如果x 和y 代幣的比例不正確（Lx≠Ly），則一些代幣將返回給流動性提供者。這與我們在Uni V2 中觀察到的行為類似。
但是對於Uni V3，它更複雜，因為我們有分段流動性函數，在刻度間隔刻度處跳躍。在下一章中，我們將展示如何在Uni V3 上以最有效的方式放置代幣。
有效的流動性提供
如果我們有一個由x 個代幣X 和y 個代幣Y 組成的投資組合，並且我們想為價格範圍 [pᵃ, pᵇ] 提供流動性，我們應該交換多少代幣X 或Y 以從中獲得最大的流動性？
為了回答這個問題，讓我們用R = y / x 來表示——我們投資組合中代幣的比率和rᵃᵇ(p)——最佳代幣比率，使得Lx = Ly。從Lx 和Ly 的公式我們可以得出：
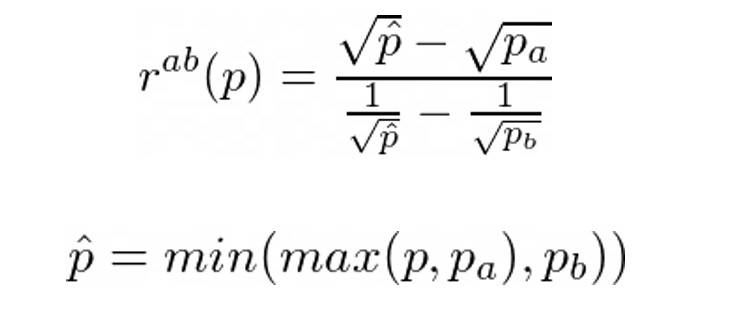
所以我們的目標是使R = rᵃᵇ。
然而，這項任務比僅僅將x 和y 對齊到指定的比率rᵃᵇ 稍微複雜一些。當我們開始將x 交換為y 或反之亦然時，池價格p 開始變化，rᵃᵇ 也是如此。這種行為如下圖所示：
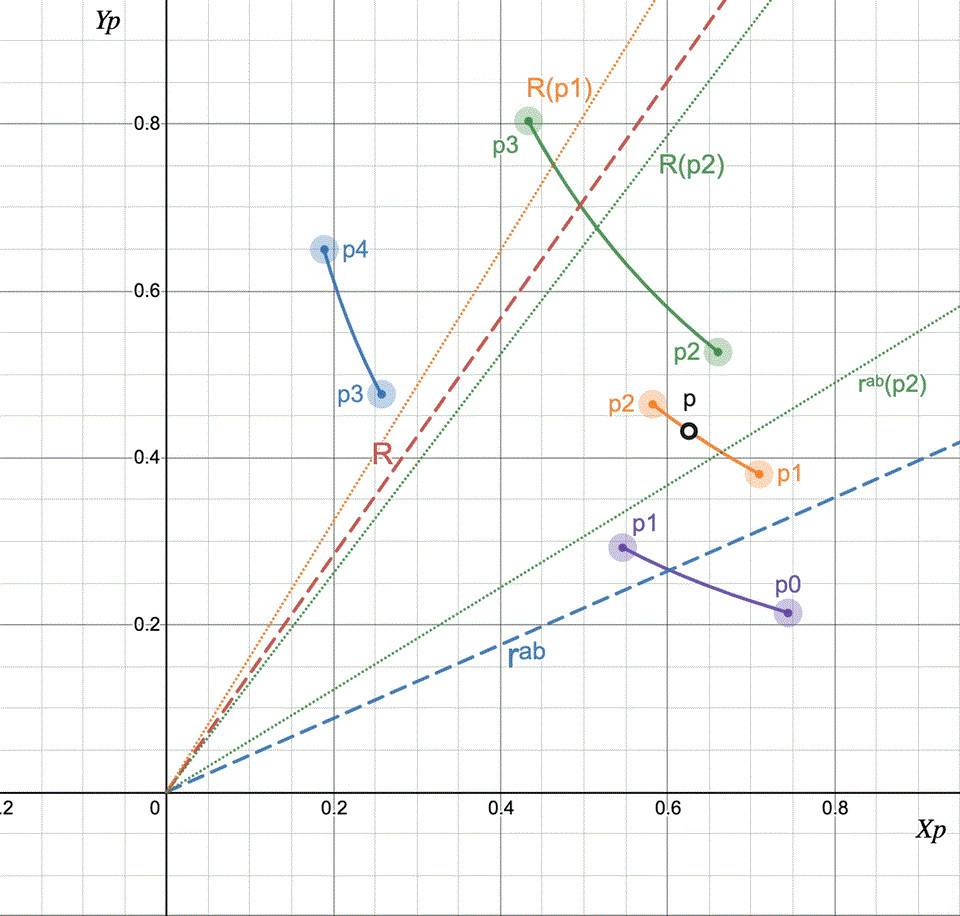
圖6：將R 對齊到rᵃᵇ
另一層複雜的是，隨著價格p 的變化以及跨越分時間隔分時池流動性L 也在變化！為了解決這個問題，讓我們首先了解在流動性L 不變的情況下，當我們用代幣Y 交換代幣X 時，比率R 如何演變。
從方程L²=xy 和p = y / x 很容易推導出：
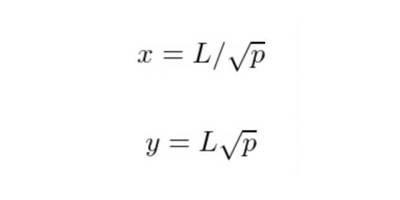
因此，如果我們用Y 交換X，從Y 中減去費用，交換後的價格結算為p₁ (p₁ > p₀)：
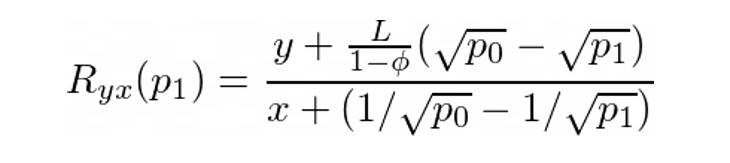
如果是用X 交換Y，則p₁< p₀，我們有：
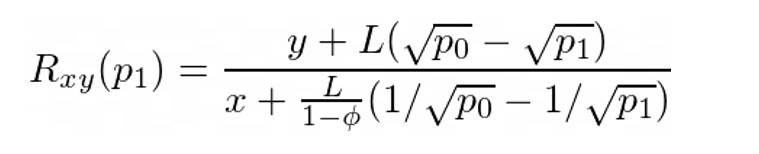
下一個問題是：
R 在什麼比率時會穿過刻度間隔以及產生流動性變化？
如果我們將R+ 表示為穿越上刻度的比率，R- 表示下刻度的比率，p₀是初始價格，p-、p+ 是各自在刻度上對應的價格，L 為刻度間隔的當前流動性，然後我們得到：
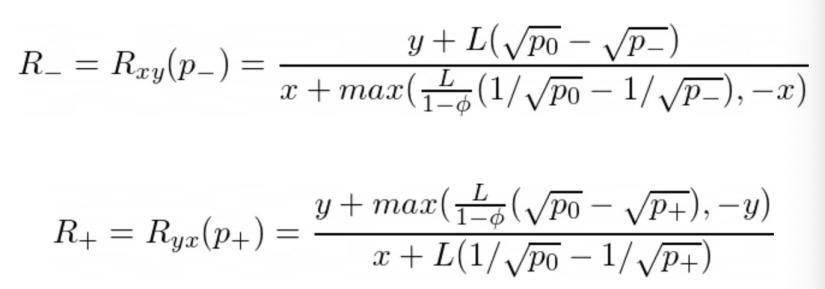
最後，我們已準備好解決問題。
首先，我們需要回答2 個問題：
- R > rᵃᵇ(p₀) 嗎？如果是，我們需要將Y 交換為X，否則的話將X 交換為Y。
- 當我們交換時——礦池價格會跨越一個刻度間隔刻度嗎？如果否- 我們可以立即解決問題。如果是-我們需要調整我們的值，就像我們一直交換到刻度間隔，然後在新的流動性上重複我們的算法。
這些問題的答案將我們帶到了4 個不同的案例中：
- 在一個刻度間隔內用Y 交換X：R > rᵃᵇ(p₀), R+ ≤ rᵃᵇ(p+)
- 在一個刻度間隔內用X 交換Y：R < rᵃᵇ(p₀), R- ≥ rᵃᵇ(p-)
- 在不同的刻度間隔中用Y 交換X：R > rᵃᵇ(p₀), R+ > rᵃᵇ(p+)
- 在不同的刻度間隔中用X 交換Y：R < rᵃᵇ(p₀), R- < rᵃᵇ(p-)
情況1：在一個刻度間隔內用Y 交換X：R > rᵃᵇ(p₀), R+ ≤ rᵃᵇ(p+)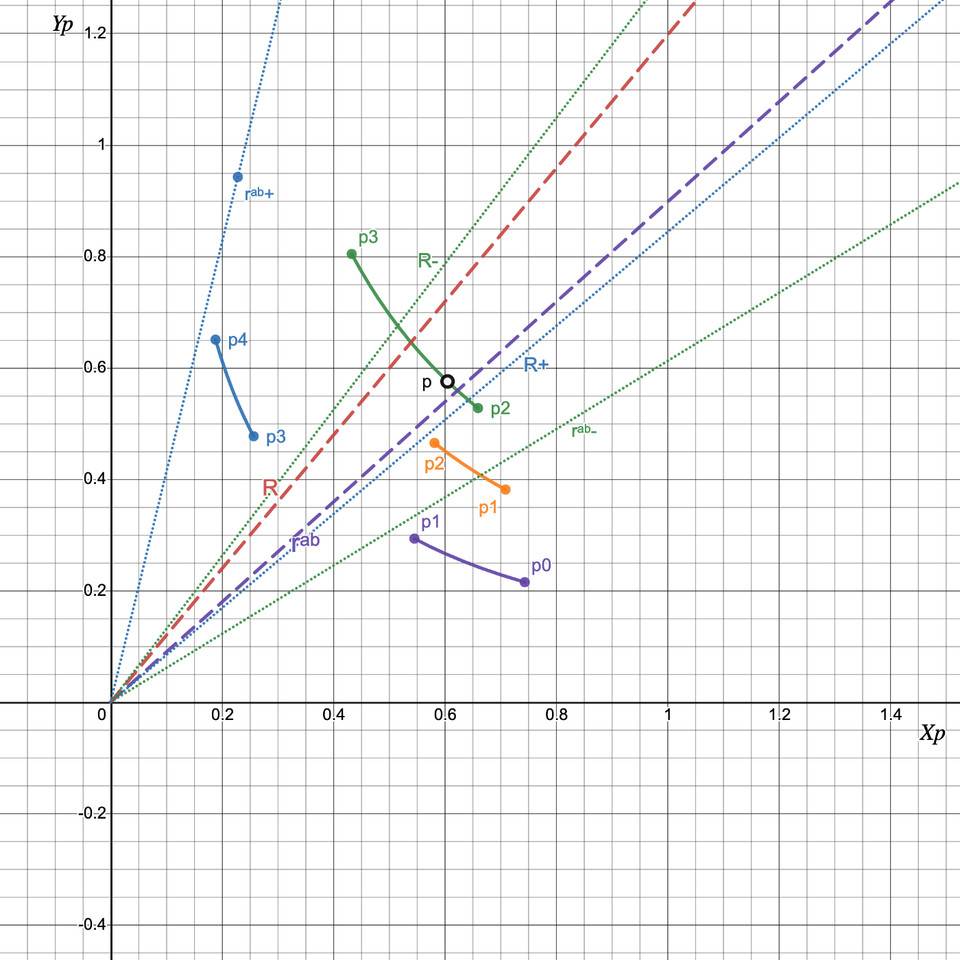
圖7：在一個刻度間隔內將Y 交換為X。當我們從Y 交換到X 時，價格增加到p₃，R 減少到R+，而rᵃᵇ 增加到rᵃᵇ+。由於最初R > rᵃᵇ 且R+ ≤ rᵃᵇ+，因此可以保證R = r 在刻度間隔內。
如果我們用y 交換x 並且交換後的價格穩定在p₁，我們只需要確保Ryx(p₁) = rᵃᵇ(p₁)：
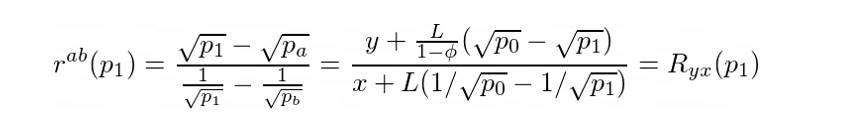
如果我們假設z = √p₁ 並重新排列方程的項，我們將得到一個二次方程：
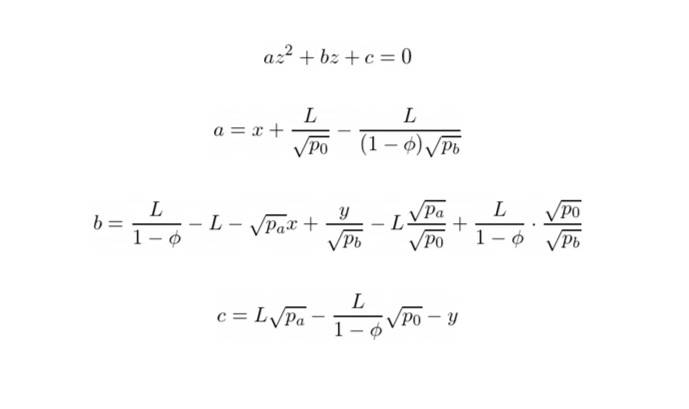
因此我們可以求解它並找到p₁：
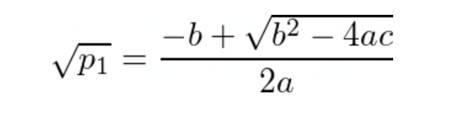
要交換的代幣Y 的數量是：
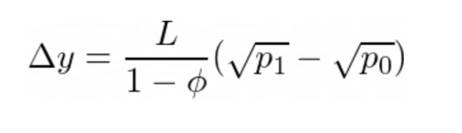情況2：在一個刻度間隔內用X 交換Y：R < rᵃᵇ(p₀), R- ≥ rᵃᵇ(p-)
圖8：在一個刻度間隔內用X 交換Y。當我們從X 交換到Y 時，價格下降到p₂，R 增長到R-，而rᵃᵇ 下降到rᵃᵇ-。由於最初R < rᵃᵇ 並且R- ≥ rᵃᵇ- 可以保證R = r 在刻度間隔內。
這種情況與情況1 非常相似，除了我們是將X 交換為Y，因此我們需要確保Rxy(p₁) = rᵃᵇ(p₁)：
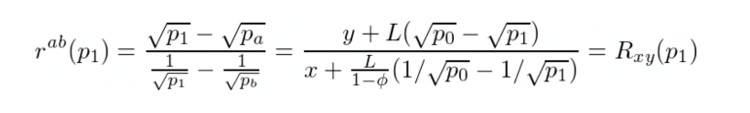
與情況1 類似，我們可以得到：
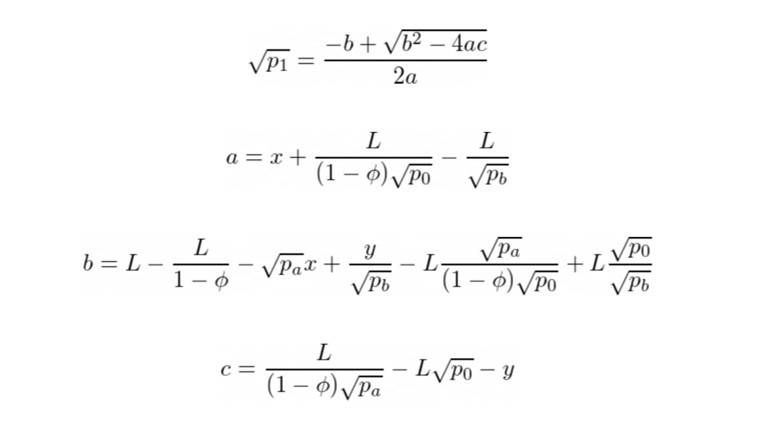
要交換的代幣X 的數量是：
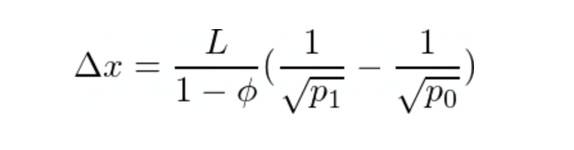情況3：在不同的刻度間隔中用Y 交換X：R > rᵃᵇ(p₀)，R+ > rᵃᵇ(p+)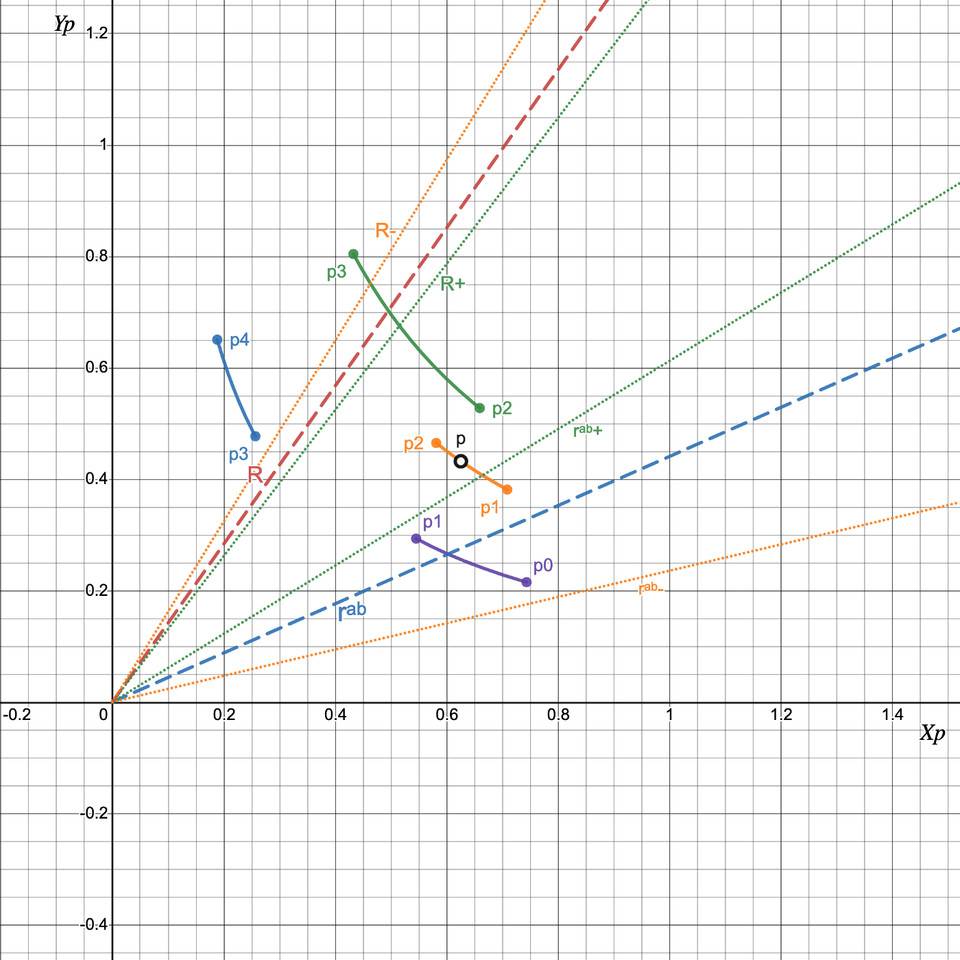
圖9：在不同的刻度間隔中將Y 交換為X。當我們從Y 交換到X 時，價格會增長到p2，然後增長到p₃，R 減少到R+，而rᵃᵇ 增加到rᵃᵇ+。由於最初R > rᵃᵇ 和R+ > rᵃᵇ+，因此當我們交換到R = rᵃᵇ 時，可以保證價格將跨越刻度間距刻度
在這種情況下，我們將Y 交換為X，直到R = R+ 並且p = p+ 並且我們處於具有新流動性的新刻度間隔中。我們記得我們交換了多少個Y 標記，以便稍後將它們添加到最終數字中。然後我們重新開始算法並重複，直到我們遇到案例1。那我們就重新定義：
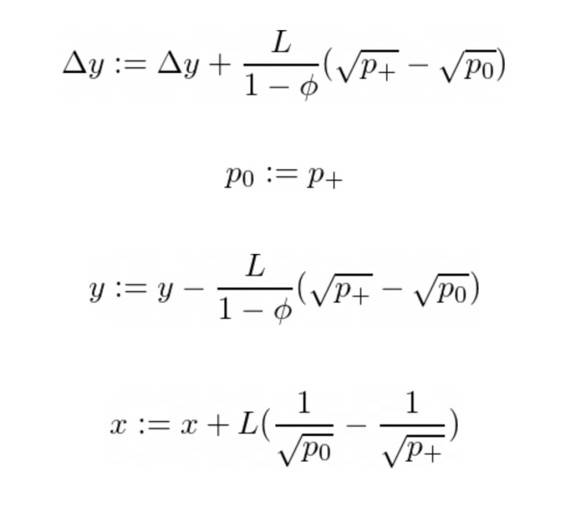情況4：在不同的刻度間隔中用X 交換Y：R < rᵃᵇ(p₀), R- < rᵃᵇ(p-)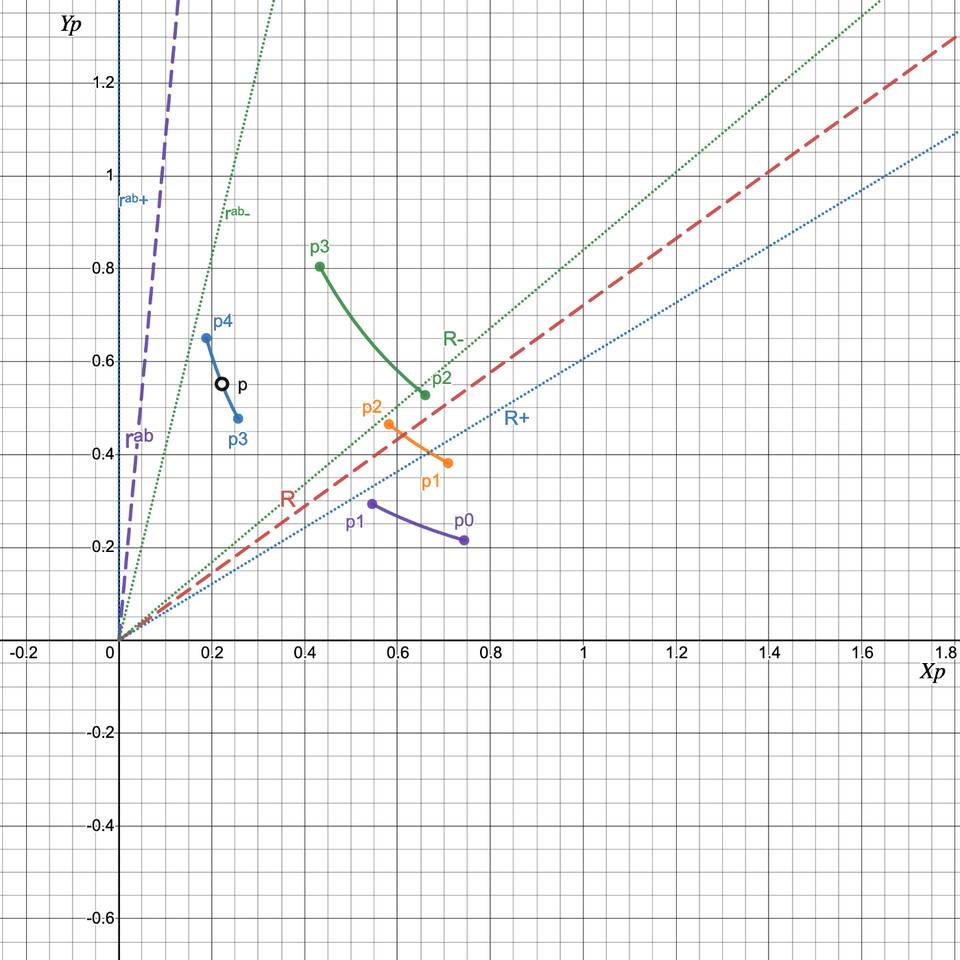
圖10：在不同的刻度間隔中將X 交換為Y。當我們從X 交換到Y 時，價格下降到p₃ 然後到p₂，R 增加到R-，而rᵃᵇ 減少到rᵃᵇ-。由於最初R < rᵃᵇ 和R- < rᵃᵇ- 可以保證在我們交換到R = rᵃᵇ 時價格將跨越刻度間距刻度
與情況3 完全相似，除了我們將X 交換為Y，直到R = R- 並重複直到我們遇到情況2。我們重新定義：
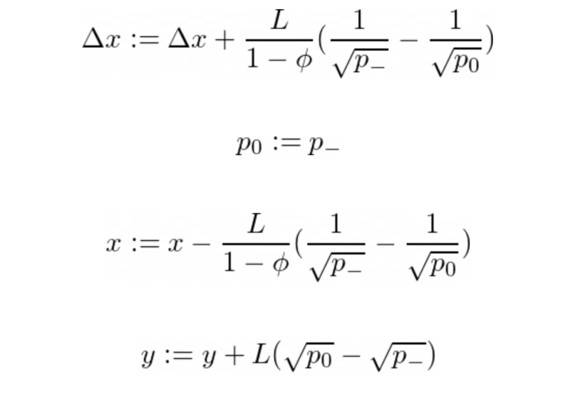
結論
在Uni V3 中以正確的比例提供流動性是一項非常複雜的任務。您需要考慮很多因素，例如刻度間隔內的不同流動性值。上面的算法描述瞭如何使用池數據來計算需要交換的代幣數量以獲得最高的流動性。
數字圖表可在此處獲得：
https://www.desmos.com/calculator/rqbrnapxbj
https://www.desmos.com/calculator/ys7kcfgjxe
https://www.desmos.com/calculator/ehdwkbtu7z
https://www.desmos.com/calculator/huzzwffze9
https://www.desmos.com/calculator/t9u9x8xgcy
在以後的文章中，我們計劃討論Uni V3 的其他有趣方面，如無常損失、多頭投資組合、策略風險等。
Mellow Protocol 正在探索AMM 的流動性提供和做市空間。您還可以在此處
查看我們的初步研究論文。 Mellow 的目標是建立一個強大的工俱生態系統，以消除市場低效率並為用戶創造成果。
我們不僅將其視為一種產品，而且將其視為複雜數學可以為DeFi 領域帶來的演變。與Uniswap 和Curve 創新用戶交易體驗的方式類似，我們相信LP 優化也在推動tradfi 的可能性。
在接下來的文章中，我們將討論有關如何實施適當的再平衡策略的更多想法，並將繼續討論DeFi 中更廣泛的主題。
特別聲明
免責聲明：本文不代表0x财经立場，且不構成投資建議，請謹慎對待，如需報導或加入交流群，請聯繫微信：VOICE-V。
來源：鏈聞
