來源| notes.ethereum.org
作者| Vitalik Buterin
譯者註:Balance attack 指的是攻擊者快速乾擾有相近算力子組的溝通。在此期間,攻擊者在一個子組發布交易(稱為交易子組),在另一個子組挖區塊(稱為區塊子組),直到區塊子組的樹以高概率勝過交易子組的樹。 Balance attack 的新穎之處在於利用GHOST 協議把兄弟塊或叔塊算入選擇區塊得分的特性。這個策略使得攻擊者可以在與網絡隔離的情況下挖一個分支,在將它的分支併入競爭區塊鏈之前影響分支選擇過程。
eth2 的分叉選擇區別於eth1 和“基於鏈(chain-based)” 的PoS 算法(例如像Peercoin 和NXT 這些舊算法,但也有像Tezos、Ouroboros 等的較新的算法) 的一個關鍵是,在eth2,有非常多影響區塊”得分(score)“的信息是並行到達的。
基於鏈的PoS 算法:
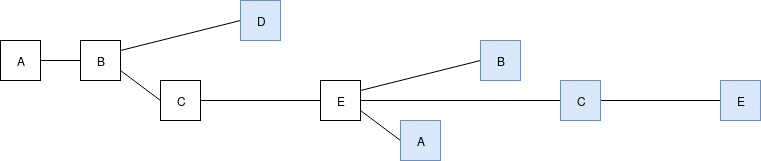
(像在eth2 裡) 每個slot 上的委員會:
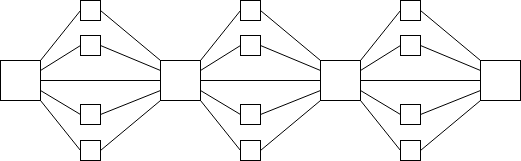
基於鏈的算法更容易證明其活性(事實上,在某些情況里活性已經被證明了),因為通常一次有一個單個行動者,使得它們充當”協作瓶頸(coordinating bottleneck)”,讓每個人都對同一個分數達成共識。
下面是基於鏈的算法中活性的”稻草人證明概述“。
假設:
- 在每個slot 裡就有一個行動者(即區塊提議者) 可以參與。
- 誠實的區塊提議者在slot 的前半發布他們的區塊
- 網絡延遲的上限是半個slot (因此是δ<1/2,以slot 為單位測量時間)。
- 被分配到在slot N+1 行動的行動者僅會基於他們在slot N 前收到的信息行動。
我們對節點收到在時間t 發出的信息的時間建模為區間(t,t+δ) 的“雲” (到這里為止,這只是陳述了同步假設的標準學術表述)。因此,存在兩種情況:
達成共識
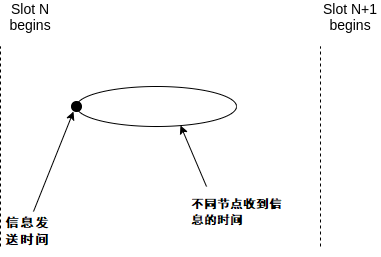
沒有達成共識

請注意,只有當在slot N 的參與者不誠實時才會出現沒有達成共識的情況。因此,如果被分配到某個slot 的參與者是誠實的,那麼要么(i) 在該slot 的末端每個參與者都對哪條是正確鏈達成共識,因為他們都是基於相同的信息計算分叉選擇的,要么(ii) 攻擊者在之前那些他們沒有參與的slot 上“用掉了” 一些儲備的參與權。因此,只有當攻擊者對每個誠實參與者有至少一個儲備的參與權時,即如果攻擊者被分到的slot 多於誠實節點時(也就是誠實大多數的假設被打破時),干擾才能繼續。
現在看看”有很多並行證明“的情況。當有很多並行證明增加一個區塊的得分時,是沒有單一行動者創造瓶頸的。因此,攻擊者可以操縱網絡(再加上有策略地對一些他們自己的驗證者廣播),以便在每個epoch 末端構建就哪些信息算入分叉選擇沒有達成共識的狀態,從而使多條鏈中的某條鏈勝出。
請看論文Ebb-and-Flow Protocols: A Resolution of the Availability-Finality Dilemma (動態協議:可用性與最終確定性兩難困境的解決方法),特別是第4 和第5 頁,那裡有對這種攻擊的說明。請注意,這種攻擊的確建基於一些在實踐中非常難以實現的網絡假設(攻擊者對個人質押者的網絡延遲有非常精細的控制),但儘管如此,一個能抵抗這種攻擊的協議還是比一個不能的協議好。
提議的解決方案
提議的解決方案是引入明確的”同步瓶頸“小工具到分叉選擇上。特別是,我們可以增加以下規則:
1. 假設所有被分配到slot N 的證明者的集體總權重為 W
2. slot N+1 裡的參與者僅會認為在slot N 末前到達(從參與者的角度) 的證明是有效的。
3. 在slot N+1 的提議者應該在slot N+1 的開端就馬上做提議。他們的提議其實是在選擇一條特定的鏈。在slot N+1 的證明者看來,如果他們在slot 進行了1/3 之前就看到提議到達了,他們會將該提案視為等同於權重為W/4 的證明(這個得分調整隻對slot N+1 有效,在slot N+1 後這個得分調整會復原)。
4. 把同步假設降低到δ<1/3
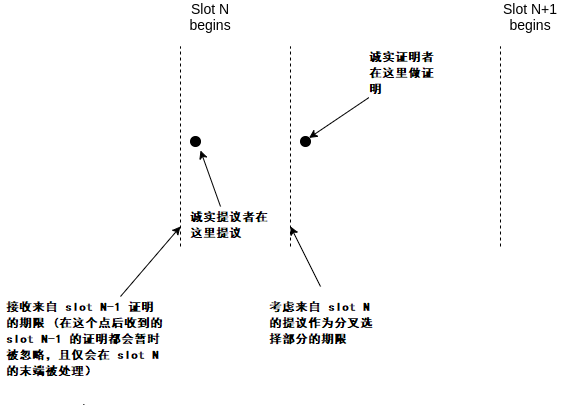
分析
(請注意:為了分析的簡易,我們假設時鐘是完全同步的,以及任何實際的時鐘差異都是網絡延遲的一部分。)
在slot 的末端,所有驗證者都已經收到一些證明集了。如果出現了攻擊(例如,有k≥1 的惡意證明者在slot N 做證明),驗證者將很可能在每個區塊的得分上有分歧。但是,他們分歧的範圍將不會超過k。假設(在不喪失一般性的情況下) 有兩個競爭區塊,A 和B,如果score(A)−score(B)≥0,則A “勝出”,反之則B 勝出。 score(A)−score(B) 的分歧範圍的上限是2k (即每個驗證者給出score(A)−score(B) 值都將在[z,z+2k] 的範圍內,z 是個固定值)。
設Wp 為提議者的權重(即Wp =上文論述的W/4)。如果提議者是誠實的,他們肯定會遵循以下兩種行為:
1. 如果他們看到score(A)−score(B)≥0,他們將提議A 區塊,否則提議B。
2. 他們將馬上提議他們的區塊,以保證所有的證明者都在期限前看到。
設 [z,z+2k] 為score(A)−score(B) 分歧的區間。我們區分三種情況:
在情況(1),提議者將給B 投票,這樣證明者將看到在 [z−Wp,z+2k−Wp] 內調整過的得分;這裡整個區間都是負數,因此對B 有充分的共識。
在情況(3),提議者將投票給A,這樣證明者將看到在 [z+Wp,z+2k+Wp] 內調整過的得分;這裡整個區間都是正數;因此對A 有充分的共識。
在情況(2),很大程度由提議者決定。取決於提議者的意見落在區間的哪個位置,提議者不是選擇A 就是B。因此,區間要么是(i) [z−Wp,z+2k−Wp],要么是(ii) [z+Wp,z+2k+Wp]。
如果是Wp≥2k 的情況,請注意從情況(2) 的定義−2k≤z<0 來看,當(2.i) z<0 且2k−Wp≤0,即z+2k−Wp 的上限是負數,也就是整個區間都是負的。當(2.ii) z>−2k 且Wp≥2k,即z+Wp>0,即整個區間都是正的。因此,充分共識是在A 還是B 取決於提議者的選擇。
現在,讓我們回到Wp= W/4 的論述中。為了避免提議者起同步瓶頸的作用,上述推理中Wp≥2k 的前提必須被打破;因此,必須有超過W/4 的證明者在每個slot 投票。
如果在任何單個slot 中提議者起到了同步瓶頸的作用,所有誠實的證明者都將往該方向投票,使score(A)−score(B) 的值與0 偏差增大。為了避免其中一方在這個點上勝出,攻擊者必須在該slot 展示足夠多的投票以與所有的誠實驗證者抗衡(減去1/4 來抵消提議者在slot 末端投票的效用);這需要遠超過W/4 的證明。
因此,要維持一段時間的失活需要至少在每個slot 上有W/4 的惡意驗證者,或≥1/4 的驗證者是不誠實的。