摘要:從數學角度深入論證比特幣分佈式賬本面對雙花攻擊的安全問題,核心是誠實節點和惡意節點在挖礦中的競爭。撰文:鄒傳偉,萬向區塊鏈首席科學家中本聰在比特幣白皮書技術部分(第6-9 頁)討論了比特幣分佈式賬本面對雙花攻擊的安全問題,核心是誠實節點和惡意節點在挖礦中的競爭。這部分內容非常重要,但中本聰的表…
從數學角度深入論證比特幣分佈式賬本面對雙花攻擊的安全問題,核心是誠實節點和惡意節點在挖礦中的競爭。
撰文:鄒傳偉,萬向區塊鏈首席科學家
中本聰在比特幣白皮書技術部分(第6-9 頁)討論了比特幣分佈式賬本面對雙花攻擊的安全問題,核心是誠實節點和惡意節點在挖礦中的競爭。這部分內容非常重要,但中本聰的表述非常簡略,省去了關鍵論證過程。區塊鏈行業中有專家對這部分內容做了說明,但都存在一些疏漏之處。本文在前人工作的基礎上,試圖給出一個嚴謹解析。
比特幣挖礦的數學過程
比特幣挖礦的本質上通過不斷運行哈希計算,以找出一個符合要求的Nonce,使其前若干位等於0。如果將Nonce 視為一個十六進制小數,那麼其可以視為一個在0 和1 之間均勻分佈的隨機變量,合格Nonce 需小於α(如果要求Nonce 前β位等於0,那麼α=2-β)。 α由比特幣算法根據全網算力調整。
用Η表示全網算力,含義是每秒可運行哈希計算的次數。用隨機變量τ表示找到合格Nonce 的時點,τ是概率論上的停時概念。因為不同次哈希計算的結果相互獨立,所以對任意t>0,

因此,隨機變量τ的累積概率分佈函數等於

(1) 表示參數為-ln(1-α)Η的指數分佈。根據指數分佈的性質,找到一個合格區塊的平均時間為

用T 表示平均出塊時間(即10 分鐘)。那麼,存在如下關係

(2) 就是比特幣的難度係數調整機制。
誠實節點與惡意節點之間的挖礦競爭
假設全網算力H 不變,誠實節點與惡意節點的算力分別為Hg和Hb,H=Hg+Hb。它們找到合格區塊的時間分別為τg和τb。根據前文的分析,和均服從指數分佈,參數分別是

誠實節點先找到合格區塊的概率是

同理,惡意節點先找到合規區塊的概率是
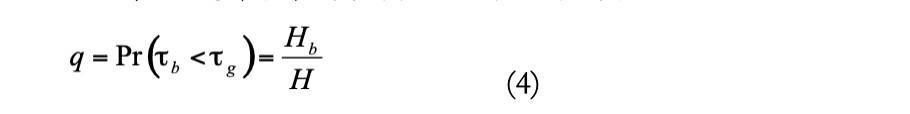
(3) 和(4) 說明,先找到合規區塊的概率與算力成正比。
惡意節點從落後追趕誠實節點的問題
假設全網算力H、誠實節點的算力Hg和惡意節點的算力Hb均保持不變。假設惡意節點落後誠實節點個區塊,接下來考慮惡意節點趕上誠實節點的概率。站在惡意節點的角度,引入如下計數函數

其中,-z 表示初始時惡意節點落後誠實節點z 個區塊。 Ii(τb<τg) 表示第i 個合格區塊是否由惡意節點生成。若是,則L(n) 增加1;否則,L(n) 減少1。換言之,L(n) 刻畫了在n 個區塊後,惡意節點領先於誠實節點的區塊數量(小於0 則表示惡意節點落後於誠實節點的區塊數量)。
惡意節點與誠實節點之間開展的是「最長鏈競爭」。用qz表示惡意節點趕上誠實節點的概率,數學表述是:

(6) 的含義是,惡意節點從落後z 個區塊出發,能超越誠實節點1 個區塊的概率。
考慮第1 個區塊的情況(i=1)。如果這個區塊由惡意節點生成,則惡意節點領先於誠實節點的區塊數量變為-z+1,此情形的概率為Pr(τb<τg)=q;反之,這個區塊由誠實節點生成,惡意節點領先於誠實節點的區塊數量變為-z-1,此情形的概率為Pr(τb>τg)=p。因此,

另外,q-1=1。但僅憑(7) 和這個邊界條件不足以求解,需要將這個問題轉換為「賭徒破產」問題(Gambler’s Ruin Problem)。
假設惡意節點在落後誠實節點N 個區塊後放棄追趕(N 是一個很大的正整數),惡意節點在超越誠實節點1 個區塊後贏得「最長鏈競爭」。這兩種情況都對應著「最長鏈競爭」停止,表示成「賭徒破產」問題是:

其中, τc也是概率論上的停時概念,L( τc)=-1 表示惡意節點贏得「最長鏈競爭」,L( τc)=-N 表示惡意節點退出「最長鏈競爭」。此時,(6) 等價於

(7) 仍然成立,但有兩個邊界條件:

(7) 可以等價表述為,

也就是

迭代可知,

將上述迭代結果累加起來可得,

(12)
考慮邊界條件(10),存在兩種情況。

第一,q>p (也就是惡意節點佔優)。因為q/p>1,所以

第二,q

(二) p=q=0.5

在上述求解過程中,N->∞的含義是惡意節點為了贏得「最長鏈競爭」可以容忍任何大的成本。這當然是一個過於理想化的假設,只考慮了惡意節點從落後追趕誠實節點在技術上的可行性。實際上,惡意節點會衡量追趕的成本和收益,在很多情況下成本超過收益,說明追趕即使在技術上可行,在經濟學上不可行。這會為比特幣分佈式賬本帶來安全保障。
這就對應著比特幣白皮書第6 頁給出的如下公式。需要說明的是,比特幣白皮書討論的是惡意節點從落後追平誠實節點的概率,而(15) 給出的是惡意節點至少超過誠實節點1 個區塊的概率。

分佈式賬本面對雙花攻擊的安全性
這是比特幣白皮書重點討論的問題。此問題的關鍵是泊松過程與指數分佈之間的關係。如果從任意時點開始統計區塊生成數量,由此得到的計數過程就是泊松分佈:
-
任意兩個不重疊的時間段內區塊生成數量是互相獨立的隨機變量;
-
在任意長度為的時間段內,區塊生成數量服從泊松分佈

換言之,在相鄰兩個區塊之間的時間間隔服從參數為-ln(1-α)H 的指數分佈時,與其對應的計數過程服從參數為-ln(1-α)H 的泊松過程。
在雙花攻擊中,假設交易發起者等待了z 個區塊。這些區塊由誠實節點生成,對應的時間等於

假設惡意節點在這個時間段內在私下生成區塊,累計生成區塊生成數量Z 服從泊松分佈,參數等於
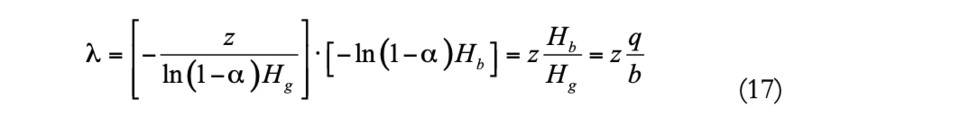
這對應著比特幣白皮書第7 頁的如下公式:

根據泊松分佈的定義,

在時0<=Z<=z,惡意節點落後的區塊數為zZ;在Z>=z+1 時,惡意節點已完成雙花攻擊。因此,惡意節點雙花成功的概率等於(只討論q