-
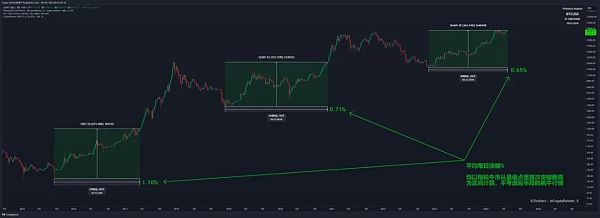
Uni v3 LP的頭寸可以分解為看跌收益和範圍組件。
-
Uni v3頭寸的值是以下兩項的和:1)空頭頭寸的總和,其值由Black-Scholes模型給;2) 範圍項,其閉合表達式由Feynman-Kac公式給出。
-
這可以通過將Uni v3 LP頭寸轉換為“固定DTE”看跌期權來進一步簡化,該看跌期權在到期時的價值收斂於T_r > 0時刻的看跌期權。
-
比較Uni v3頭寸的預期收益和期權溢價可以幫助確定持有Uni v3頭寸或將其“出借”給期權買家是否更有利。
為了建立Uniswap v3 LP頭寸,必須在用戶指定的範圍內鎖定資產(例如ETH),在用戶指定的範圍(由低刻度tL和高刻度tH定義)之間。該Uniswap v3 LP倉位的取值為:
其中,S是資產的現金價格,K是執行價格√(tL*tH), r是范圍因子√(tH/tL)。範圍因素決定了持有資產和numéraire之間的過渡有多“尖銳”。
那麼多頭期權呢?如果一個人能夠借入一個Uni v3 LP頭寸,並在以後償還,這相當於購買了一個看跌期權。用戶在藉入LP頭寸時將支付固定的溢價。

溢價應該是多少?我們能否使用Black-Scholes模型這樣的既定框架來直接為Uni v3頭寸定價?
答案是肯定的。
在這篇文章中,我們將展示如何將V(S)分解為一個短線看跌組件(對應於一個單刻度頭寸)和一個範圍組件(僅存在於上/下刻度之間)來實現這一點。
Feynman-Kac的期權定價
在推導Uni v3期權的價格之前,有必要回顧一下常規期權的定價方式。利用Black-Scholes模型,有許多方法可以得出常規看漲期權的價格。我最喜歡的方法是使用Feynman-Kac公式,該公式表示期權u(S,t)的值為:

其中V(x, T)是到期時的收益函數,平均⟨ ⋅ ⟩ 是幾何布朗運動的概率度量。
理解Feynman-Kac公式的含義很簡單:期權在T時刻的價值是通過計算從現在到未來T時刻所有可能價格變動的收益函數的平均值來確定的。
物理學家Richard Feynman最初在量子力學的路徑積分形式中提出了一個類似的方程,在這個方程中,一個粒子的“預期”頭寸是由該粒子可能採取的所有路徑的加權和決定的。 Mark Kac意識到他們正在研究一個類似的問題,當時他們都在康奈爾大學,他聽了Feynman的演講,那次合作產生了Feynman-Kac公式。
因此,直接計算Feynman-Kac 公式,得到:

對於看漲期權,收益V(S,T) = max(SK,0),對於看跌期權,收益V(S,T) = max(KS, 0),因此,時間t 的看漲看跌期權的價值為:

要證明這與Black-Scholes定價相一致。
定價Uniswap v3期權
Feynman-Kac公式使計算奇異期權的價值變得容易。我們將應用Feynman-Kac公式來計算Uniswap v3期權的值。
為了讓事情變得簡單一點,我們首先將Uni v3 LP的價值分解為兩個不同的部分V(S, t) = V_p(S, t) + Vρ(S, t),其中V_p=-max( KS, 0) 是看跌期權的收益,範圍收益Vρ是由以下式給出的:

我們可以圖形化地看到看跌期權和範圍收益如何與Uni v3頭寸的價值相關:範圍收益在執行價格時是最大的,在上/下刻度處為零(為了簡單,我畫出了範圍收益的負值)。

使用這個分解,我們可以使用Feynman-Kac公式明確求解在時間t的Uni v3期權的值。這樣做,我們得到:

其中,Put(S, t) 是Black-Scholes 給出的執行K 處的時看跌期權的熟悉價格。
“範圍期權”ρ(S,t)分量是嚴格正項,對應於LP頭寸的範圍部分的值。通過求解Feynman-Kac公式,得到了ρ(S,t)的一個相當複雜的表達式:

雖然我們現在對ρ(S,t)的細節不感興趣,但我們可以從圖形看到,ρ(S,t)是這樣的:

我們能讓這個表達式更簡單嗎?
Uni v3頭寸值的表達式相當複雜。幸運的是,我們可以大大簡化分析。
正如我關於在Uniswap v3中創建永久期權的文章所示,一個具有範圍因子r的Uni v3 LP頭寸的良好近似是在時間T_r的常規看跌期權,其中
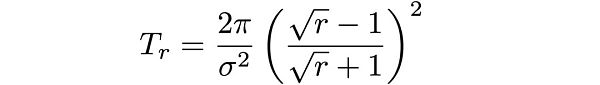
因此,我們可以將Feynman-Kac公式給出的期權定價表達式簡化為一個更簡單的表達式,該表達式利用了上面的範圍因子/DTE關係。具體來說,我們得到:

換句話說,Uniswap v3期權的值相當於一個以固定的到期天數(DTE) 到期的看跌期權,因此在到期時DTE >為0。
在到期前,Uni v3期權的價格仍然受theta衰減的影響,但gamma將被限制在45DTE期權的gamma。
这个近似有多精确?我们可以在下图中看到,将固定DTE近似值与Uni v3期权的计算值进行比较,当范围因子小于2时,固定DTE看跌期权近似值与精确解之间的差异并不显著:

Uni v3的返回值是否匹配它們的“期權”值?
目前,對於Uni v3的LP來說,唯一的選擇是持有他們的頭寸,直到他們積累了足夠的費用來盈利。沒有協議允許用戶輕鬆地借入/出借Uni v3 LP頭寸。
但是,如果有這樣的一個協議,那麼Uni v3 流動性提供者藉出其LP 頭寸所收到的溢價將由Black-Scholes 模型給出,該模型具有取決於範圍因子r 的“固定DTE”。相比之下,如果不考慮頭寸並簡單地收取費用,費用也會累積。
因此,在Uni v3 LP頭寸被鑄造/出借/借入並作為期權交易的世界中,一個關鍵的問題是,是否這樣做會更好:
持有LP頭寸一段時間T,收取0.05- 0.3% -1%的費用
或
“出借”期權期限為T,收取固定的保費
讓我們通過分析這兩個場景的預期收益率來探討這個問題。
保持LP頭寸
首先,如果將流動性部署到單次報價,則單位流動性ΔL 的預期LP 回報為:

其中γ是費用等級(如:0.01、0.003或0.0005),“Tick Liquidity”是當前價格池中的流動性數量。 √(8/π)=1.5957691216…的因子來自假設價格遵循幾何布朗運動的情況下推導出在價內花費的時間。
這裡的關鍵是,預期收益的增長是√T。因此,由於對於更廣泛的頭寸,費用隨時間線性累積,我們將只考慮單點頭寸。
重要的是,這意味著LP回報將取決於池的總規模和部署的tick 處的總流動性。
在下面的示例中,我們考慮在ETH-DAI-0.3%池中的3990刻度處部署一個頭寸。由於該池的日交易量為1571萬美元,3990點的鎖定價值為70.60ETH = 281694美元,相對LP回報應該是每√天約1.6%或每年約30%(假設年化波動率為100%)。

相比之下,將相同的流動性配置到ETH-USDC-0.03%這類資產池中,LP頭寸每√天的回報率為1.37%,即每年26.2%。一些池子產生的收益比其他池子多。
一些池的預期回報率非常高,主要是因為與交易量相比,它們的每點流動性相對較低。
例如,一個新上市的代幣,如RBN,在當前的價值為2500萬美元的情況下,只有50萬美元的鎖定價值。

向期權買家出借Uni v3 LP頭寸
另一方面,用戶可能希望創建一個Uni v3 LP頭寸,並將其借給另一個用戶一段時間T 以獲取溢價。
具體而言,收到的保費將為:

除了時間按照t→(t+T_r)轉換外,這是對空頭看跌期權價值的熟悉表達式。
這個表達式將取決於特定的底層證券,執行價格K,隱含波動率σ和到期時間t .如果我們認為期權是“平價”鑄造的,LP頭寸執行價格的K等於當前價格,然後看跌期權的價值是:

有趣的是,這個表達式也依賴於時間的平方根。這意味著我們可以直接將每單位部署流動性收到的溢價與通過持有LP 頭寸和收取費用獲得的預期回報進行比較。
如果我們考慮一個單次報價倉位,那麼T_r將為0,(Tt)將是該倉位的持有時間(如果持有至到期)。
因此,我們只需要比較√T項相乘的因素,就能找到哪種策略最有利:

假設年波動率為100%,這意味著如果每日交易量/即時流動性比率大於以下值,持有期權只會產生大於借出期權的回報:

可能需要計算每個池的實際日交易量、tick流動性和已實現的波動性,以準確判斷是否滿足上述標準(每個池可能會發生變化)。

與它們鎖定的流動性相比,一些池子的日交易量確實很大。只有當持有比率大於1時,持有這些資產池的頭寸才會產生高於期權溢價的預期收益。
目前,只有上面強調的UNI/ETH, HEX/USDC和RBN/ETH池可以產生更高的投資回報。持有比率< 1 的任何貨幣對都會表現不佳,將它們作為期權出借。
換句話說,將大多數Uni v3交易對的Uni v3 LP頭寸作為ATM期權出借,比持有+收取費用更有利可圖。
要點
我們的結果表明,Uni V3頭寸類似於賣空看跌期權,在大多數情況下,將其借給期權買家並收取溢價,而不是簡單地持有它並收取費用。
這意味著什麼?首先,這表明,建立一個基於Uniswap v3(或SushiSwap即將推出的集中流動性池)的健康期權市場,可能會增加流動性提供者收集的收益率。
其次,LP不僅可以產生更多的收益,期權買家還可以通過購買看跌期權來保護自己的投資。 ETH-穩定幣對期權可以有效地由Opyn、Pods Finance或Lyra Finance等協議有效處理,但它將挑戰建立智能交易合約存在的每個可能的資產對的期權(成千上萬的市場存在Uniswap長尾結束的加密資產)。
最後,人們在解釋Uniswap v3或SushiSwap上集中流動性頭寸部署的方式時,需要進行文化上的轉變。雖然恆定產品AMM 更易於理解和管理,但與集中流動性AMM 相比,它們容易出現重大的非永久性損失,並且資本使用效率非常低。
做空期權交易本質上是一種有利可圖的行為(因為隱含波動率往往高於實際波動率),但管理做空期權投資組合不是一種買入並持有的被動策略。做空期權和Uni v3 LP頭寸必須被積極管理,但積極投資並不意味著每天每時每刻都在觀察圖表和交易。有了正確的工具,成為一個積極的投資者每天只需要不到5分鐘。
來源:https://lambert-guillaume.medium.com/pricing-uniswap-v3-lp-positions-towards-a-new-options-paradigm-dce3e3b50125