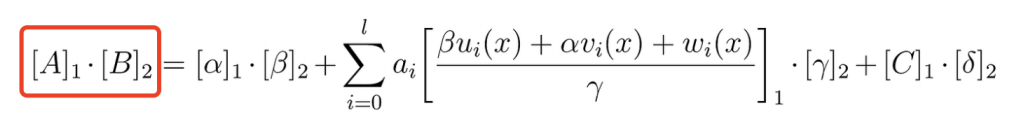Groth16 存在延展性攻擊風險,可通過簡單的計算偽造出新的證明,實際運用中需要注意防止出現雙花攻擊。
By: 大醬
前言
之前的文章我們盤點了ZKP 主流實現方案技術特點,我們提到了一些ZKP 算法存在延展性風險,本篇我們繼續從實戰角度為大家展示它的攻擊原理及防禦方法。
漏洞簡介
ZKP 的延展性攻擊,是指給定敵手一個合法證明,敵手在不知道見證的條件下自己生成新的合法證明。
並不是所有的證明系統都存在延展性攻擊風險,實際上這個問題目前主要存在於Groth16 證明系統中。那麼問題來了,目前已經有那麼多的證明系統,為什麼還要堅持使用Groth16 呢?其實也沒得選擇,Groth16 生成的證明體積實在是小到極致,驗證也極其之快,在計算代價十分昂貴的區塊鏈上,使用Groth16 似乎是最理想的選擇。
延展性風險會帶來哪些風險呢?我們可以想像一下如果有這麼一個存款系統,它使用用戶提交的ZKP 證明來驗證其身份,驗證成功則可以提款。由於這個系統的驗證過程是公開的,任何人都可以獲取到這個證明,如果我們是用證明值本身做為取款登記,如果這個證明被獲取到並進行變換,那就可被利用來多次提款。漏洞的利用需要看具體的場景,但我們可以看到延展性首先會帶來雙花的風險。
數學原理
理解攻擊原理我們首先需要從理解算法開始,這需要有一定的密碼學基礎,感興趣的同學可以自行尋找Groth16 算法資料。這裡我們直擊漏洞根源:驗證函數。
我們來看一下這個驗證函數公式:
如果沒有對這些字母一一從頭介紹,我想很難看懂它在表達什麼,但我覺得過多的介紹是不需要了,記好公式左邊的“A 乘B” 就這麼簡單,然後我們開始施展數學魔法。咒語如下:

根據群的結合律,那麼上面公式中:
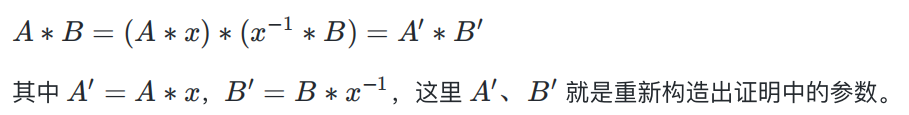
這只是其中一種比較簡單的構造方法,另外還有一種構造方法 [1],這裡不做闡述,因為我們已經得到想要的東西了。
工程實現
有了上面的公式,就可以在工程上實現Groth16 證明的延展。選擇一個要偽造證明的對象,獲取它的proof,例如:
{ pi_a: [ ‘17566212007750634279332191898019870443899908963707812937725971557556988121113’, ‘13653824972036797689593667463260040326059024360787769597142078414930263663703’, ‘1’ ]pi_b: [ [ ‘14906111038352923510344648516413952434168552622848767570599399834157918236589’, ‘15289017543994496306320102143103349779456992442925111629326024552687168229256’ ], [ ‘18841235948006283310515755114762069779103481848435391875780416574913227842443’, ‘6835281862874020275059416795628130939104366467185014410026268177455413514889’ ], [ ‘1’, ‘0’ ] ], pi_c: [ ‘21641806348662631815866837255154640732047306895903168385641666607914783128458’, ‘2082587994352117459125871298218148663854896572836176277773049196516560449682’, ‘1’ ]protocol: ‘groth16’, curve: ‘bn128’}
我們看這樣的一個proof,pi_a, pi_b, pi_c 就是上面公式裡描述的A, B, C,這個證明使用的是BN128 曲線,然後我們需要去尋找支持BN128 曲線開發庫。這裡我們選擇ffjavascript,它是一個基於Javascript 的有限域庫,支持BN128, BLS12381 曲線。
首先,我們任意構造一個域上的元素及它的逆元:
const X = Fe(“123456”);const invX = F.inv(X);
然後,分別相乘,核心代碼如下:
const A = curve.G1.fromObject(proof.pi_a);const B = curve.G2.fromObect(proof.pi_b);new_pi_a = curve.G1.timesScalar(A, X); //A’=x*Anew_pi_b = curve.G2.timesScalar(B, invX); //B’=x^{-1}*B
最後,用new_pi_a, new_pi_b 去替換原proof,得到新的proof:
{ pi_a: [ ‘6515337738552169645617263495374285821912767490069335826295120714428977813009’, ‘10671874016637483602721966808912960491553808325993800847672325376634242358838’, ‘1’ ]pi_b: [ [ ‘20523135654483520737281403147507843211011765855706506084021355785019229409285’, ‘4032527486736971273144842057682931136787425732029780739716144011227563817375’ ], [ ‘9389285843105460816015935120908213706233585149018458753845466963847282799614’, ‘7207137211649923819130654483456848273137049778520784010268635580504303221849’ ], [ ‘1’, ‘0’ ] ], pi_c: [ ‘21641806348662631815866837255154640732047306895903168385641666607914783128458’, ‘2082587994352117459125871298218148663854896572836176277773049196516560449682’, ‘1’ ]protocol: ‘groth16’, curve: ‘bn128’}
至此,我們已經成功構造出了新的證明,把proof 放到驗證函數中去驗證可以發現它能通過驗證。
防範
如何防範Groth16 延展性攻擊呢?可以參考這四種方法:
對proof 進行簽名,驗證者在驗證proof 同時也驗證簽名是否正確;
參考TornadoCash 在電路的公開輸入中增加nullifier 值,nullifier 確保證明對應的公開輸入只能被使用一次;
在電路中將證明者的身份信息(如以太坊的msg.sender )加入到公開輸入中,然後驗證者就可以對提交證明的人進行身份驗證;
使用其它的證明系統,參考我們之前的文章。
總結
Groth16 存在延展性攻擊風險,可通過簡單的計算偽造出新的證明,實際運用中需要注意防止出現雙花攻擊。
參考鏈接:
[1]. https://medium.com/ppio/how-to-generate-a-groth16-proof-for-forgery-9f857b0dcafd
往期ZKP 系列:
慢霧:盤點ZKP 主流實現方案技術特點
ZKP 系列之Circom 驗證合約輸入假名漏洞復現
展開全文打開碳鏈價值APP 查看更多精彩資訊