這篇文章將展示基於2-of-2 MPC 技術的MACI 匿名化方案的具體實現。本文核心內容主要分為三個部分:從任意算法到邏輯電路的實現;從邏輯電路到混淆電路的實現;利用不經意傳輸實現多方安全計算。最後,我們總結基於多方安全計算的匿名化方案。
感謝Felix Cai 對MACI 和隱私投票中多個問題的討論。
這篇文章將展示基於2-of-2 MPC 技術的MACI 匿名化方案的具體實現。本文核心內容主要分為三個部分:從任意算法到邏輯電路的實現;從邏輯電路到混淆電路的實現;利用不經意傳輸實現多方安全計算。最後,我們總結基於多方安全計算的匿名化方案。
算法
在MACI 系統中,操作員Operator(記為O)管理著一個數組,這個數組記為deactivate[],其元素個數與registry 數組中的元素個數相同。數組中每個位置的編號代表了key 值(用戶的編號),而每個位置存儲著對應的公鑰。為了更好地理解deactivate[] 數組,可參考如下例子:在deactivate[] 數組中,假設registry 中的用戶1(deactivate[] 數組中的第一個元素)發起了deactivate key 操作,操作員O收到該操作請求後,如果操作的合法性被O承認,O在deactivate[] 數組中的第一個位置填入registry 數組中第一個位置所包含的value 值(用戶2的公鑰)。另外,假設用戶O沒有發起deactivate key 操作,那麼deactivate[] 數組中的第二個元素的值為0。這樣一來, deactivate[] 數組的元素個數和registry 數組中的元素個數相同就可以理解了。
現在,為了實現MACI 系統對管理員的匿名性,需要設計一個2-of-2 的MPC 方案來實現以下兩個性質:
先暫且不考慮這兩個要實現的目標。先考慮更換密鑰的操作: A發起更換deactivate[] 數組中屬於A的公鑰的請求,O驗證A的請求是否合法,如果合法,則執行更換公鑰操作;否則,拒絕請求。

根據上述邏輯,我們先設計一份偽代碼來實現這個操作,如下:
function findElement(array, PK_1, PK_1′) { for (let i = 1; i < array.length; i++) { if (array[i] === PK_1) { return PK_1′; } } return false;}
fn find_element(array: &[i32]a: i32, b: i32) -> bool { let mut result = false; for i in 1..array.len() { result = result || (array[i] == a && b == a); } result}

邏輯電路的生成原理
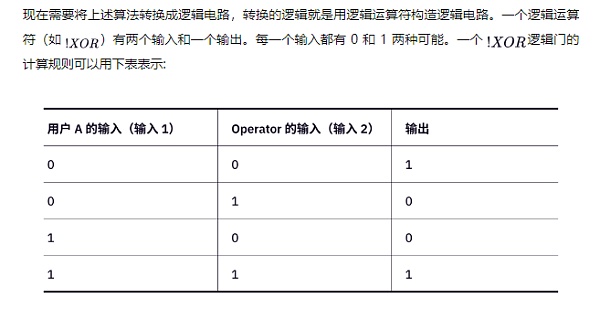

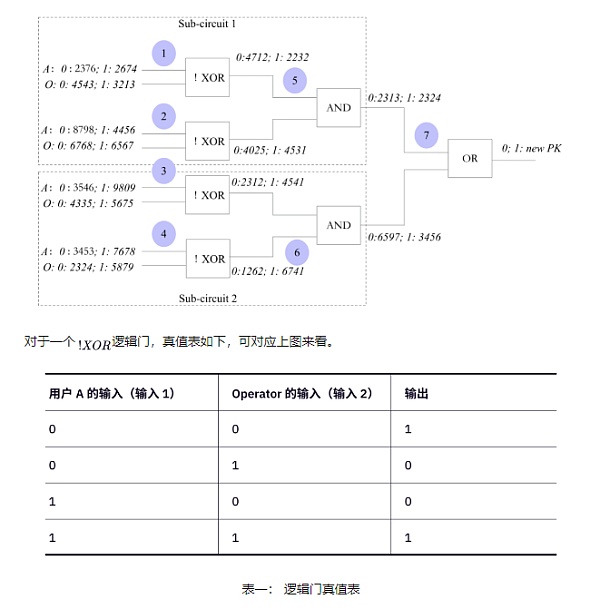
為了簡單起見,暫且假設一個公鑰由二位二進制數來表示(實際的公鑰是256 位二進制數)。那麼,現在就需要用用戶A的輸入公鑰,對比deactivate[] 數組中的二把公鑰。因此,需要對比二次。
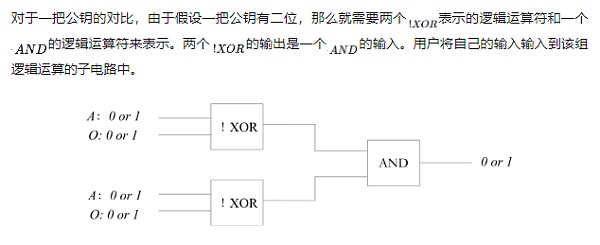
邏輯電路由邏輯門組成,邏輯電路中的邏輯門被分為 層,比如上面的電路是兩層。邏輯門第一層需要用戶來添加輸入, 其他層是中間節點,最後是根節點。對於用戶輸入的邏輯門,有兩個輸入和一個輸出。其中一個輸入由用戶A完成。另外一個由O完成。這三個邏輯門組成了一個子邏輯電路。這個子邏輯電路負責一次公鑰的對比。
邏輯電路的生成工具
在現實中,為了讓一個固定的算法轉換成邏輯電路,需要用到一些工具,如
1.Verilog HDL 和VHDL:這兩種硬件描述語言被廣泛用於數字電路的設計和仿真,可以使用它們來描述算法的行為,並將其轉換為邏輯電路的形式。這些語言都支持從高級語言(如C、C++ 和Java)轉換為硬件描述語言的形式。使用Verilog 或VHDL 需要一定的硬件設計和編程經驗。
2.Xilinx Vivado Design Suite:這是一款商業軟件,用於FPGA(現場可編程門陣列)的設計和開發。它提供了一個綜合工具,可以將高級語言或RTL(寄存器傳輸級)代碼轉換為邏輯電路的形式。它支持多種編程語言,包括C、C++、SystemC、Verilog 和VHDL 等。
3.Yosys:這是一款開源的EDA(電子設計自動化)工具,用於數字電路的設計和仿真。它支持從Verilog 和VHDL 等硬件描述語言轉換為邏輯電路的形式。它也支持從高級語言(如C、C++ 和Python)轉換為RTL 代碼,然後轉換為邏輯電路的形式。
混淆電路(Garbled Circuit)
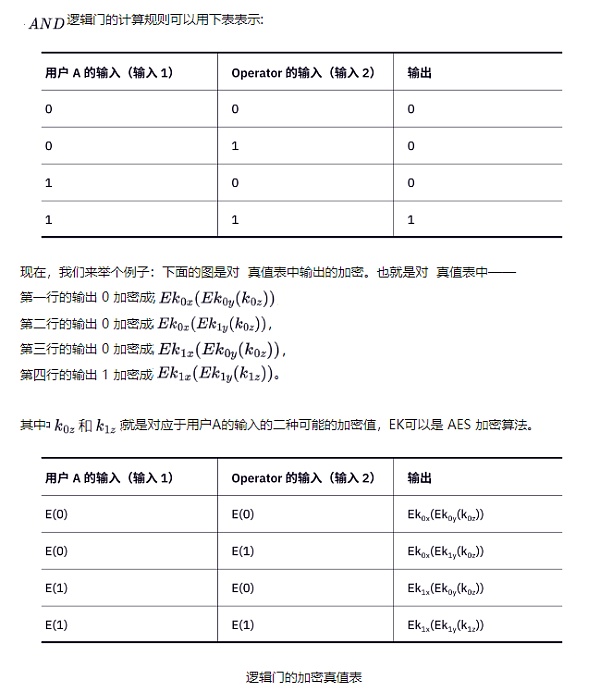
邏輯門的加密(混淆)
回到現在的例子中,因為我們的公鑰在deactivate[] 數組中都是有序號的(序號等價於用戶的編號),且數組deactivate[] 中的最大元素個數是有上限的(用戶的個數)。因此,假設最大元素個數是N,那麼,就需要構建N個子電路,然後合成一個最終的邏輯電路。
由於邏輯電路在每一個epoch 中(一個epoch 是區塊鏈更新registry 中元素的一個週期)是固定的,那麼,所有用戶都可以使用這個早已經生成好的,並存儲在區塊鏈中的邏輯電路。在本文例子中,由於deactivate[] 數組中只有兩個元素,因此子電路只有兩個(每個子電路對應於一次公鑰的對比)。
注:在一個epoch 中,registry 數組中元素個數是固定的,因此用戶的輸入和數組中的元素的對比次數是固定的,因此邏輯子電路的個數是確定的,且邏輯子電路是事先可以確定好的,因此整個邏輯電路是唯一確定的。
接下來,就是將邏輯電路的每一個輸入進行加密,然後將每一個邏輯門進行混淆。
先考慮加密。加密這個動作是由用戶A完成的。他對每一個輸入和輸出的0 和1 用加密值表示。注意,最終的根邏輯門的輸出不需要進行加密,在本案例中,就是0(對比失敗),和1(更換新的公鑰)。如圖所示:
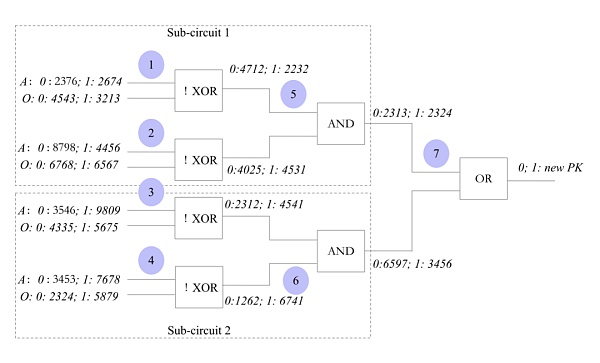
邏輯電路中的每一條引線的0 和1 都用加密值代替。同時,每一個邏輯電路都有一個固定的編號(這個是所有人都已知的)。例如,編號1、2、5 就構成了一個子電路1(比較用戶的公鑰和數組中的第一把公鑰)。
基於此,將邏輯電路的每一個邏輯門的輸入和輸出(除了根邏輯門)進行加密後,在Operator 的視角里,對於加密後的邏輯電路,他就不知道每個邏輯門的輸入數字(加密值)對應的明文(是0 還是1)。
輸入加密的方法
在混淆電路中,為每個輸入值生成兩個隨機key 的過程通常是使用偽隨機數生成器(PRNG)來實現的。常用的生成隨機key 的實現和庫有很多,例如OpenSSL、Crypto++、libsodium 等。
輸出加密的方法
基於偽隨機函數PRF 的方法是Yao 的混淆電路中實現對輸出二進制數0 和1 的加密的主要方法之一。具體來說,這種方法可以實現對每個邏輯門的輸出進行加密,保證了數據的機密性和可靠性。
在基於PRF 的方法中,每個邏輯門的輸出都被混淆成為一組包含多個label 的二元組,其中每個label 都是一個隨機的01 字符串。在生成每個label 時,可以使用偽隨機函數(PRF)來實現。具體來說,可以使用一個密鑰和輸入值(如0 或1)作為PRF 的輸入,然後得到一個隨機的01 字符串作為label。由於PRF 是一種可以模擬真正隨機數的算法,因此生成的label 具有高度的隨機性和不可預測性,保證了數據的機密性和安全性。
在混淆輸出時,可以將每個邏輯門的輸出表示為一個包含兩個label 的二元組(如{label0, label1})。其中,當輸入為0 時,使用label0 作為輸出;當輸入為1 時,使用label1 作為輸出。在將邏輯門的輸出發送給下一個參與方時,只發送一個包含正確label 的二元組,保證了數據的機密性和保密性。常見的PRF 包括HMAC、SHA、AES 等。
需要注意的是,對邏輯門的輸出採用上述方法的目的是為了便於不經意傳輸(oblivious transfer)的實現。
這裡其實就可以推導不經意傳輸過程了。比如,用戶A 將這四個輸出——

用戶A 輸入的生成
現在,我們繼續假設,用戶A公鑰的編號是1,數值是10,而數組中的二把公鑰(編號分別為0、1)的數值分別是11, 10。也就是說用戶A的公鑰在數組中。
接著,用戶將自己的輸入,分別輸入到兩個子電路中(sub-circuit 1 和2)。用戶在第一個邏輯子電路(1、2、5)中進行輸入。他的輸入是:在編號為1 的邏輯門輸入2674(代表二進制數1);在編號為2 的邏輯門輸入8798(代表二進制數0)。用戶在第二個邏輯子電路(3、4、6)中進行輸入。那麼,他的輸入是:在編號為3 的邏輯門中輸入9809(代表二進制數1);在編號為4 的邏輯門中輸入3453(代表二進制數0)。

電路混淆
接下來的步驟就是將邏輯電路進行混淆。
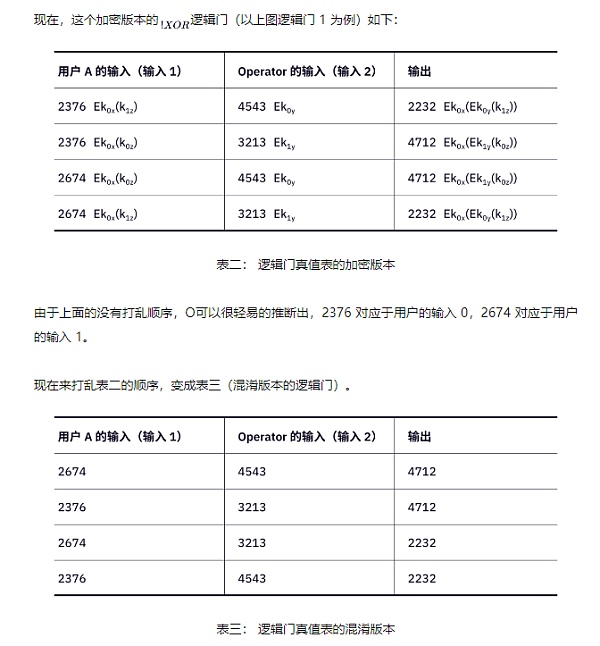
這樣一來,根據這個表格的排序可能性,O想通過表三還原成真正的表一,會碰到4 種可能性。那麼,如果在一次證明中涉及到N個邏輯門,每個邏輯門用戶A都做上述操作,那麼就有4N種可能性。這樣,通過排序任意顛倒,使得O很難推斷出每個數字到底代表0 還是1。
第一次通信

不經意傳輸(Oblivious Transfer)

此時,我們需要回顧兩個一定要保證的性質:


上述三個步驟,滿足了第二個性質,但是沒有滿足第一個性質,也就是說,O在解密了其中一個加密值後,得到了明文1,但是,也暴露了另一個明文0。這樣一來,混淆邏輯門表就暴露了很多信息給O,這樣讓O有機會破解A的秘密,從而使得性質1 無效。

從對一個邏輯門的OT 通信可以看出整個OT 通信的全貌,即每個邏輯門的OT 通信都是如此,且在一次OT 通信過程中全部完成。這樣,O就能得到所有葉子邏輯門的輸出,這樣他就能進一步得到分支邏輯門的輸出,從而最終得到根邏輯門的輸出。
方案改進
上述方案中,需要且可以改進的地方有很多。例如,改進算法設計,降低算法的複雜度;改進邏輯電路的設計,讓邏輯電路變得更加簡單(減少門的個數,減少通信是需要傳遞的信息);增加方案的安全性,加大破解方案的計算複雜度;讓交互變成非交互。
算法和邏輯電路的改進

但是,如果採用Merkle Patricia Tree 的數據結構的話,對比的次數要少很多(這是因為對於256 位的公鑰來說,形成的MPT 一定是稀疏的,因此,可能篩選二到三輪就可以篩選出想要的值)。那麼,一旦算法計算複雜度下降了,邏輯電路的設計也就要簡單很多。
邏輯電路的設計也有化簡的可能性。

A的每個輸入都不同,O也是。實際上,可以進行化簡。變成如下圖所示。
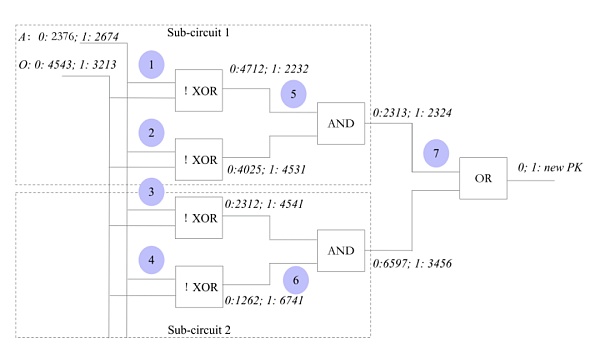
這樣的化簡可以讓輸入變少。
增加安全性

如果O想輸入的是0,那麼他得到的結果必然是0,也就是說,他天然知道輸出0 的加密值,那麼他就天然知道了1 的加密值。同時,由於A的輸入已經是確定的,那麼他可以根據A的輸入值,和1的輸出的加密值所在的行,去分析,如果1 的輸出的加密值所在的行,不包含A的輸入加密值,那麼A的輸入就是0,否則就是1。
為了解決這類問題,我們需要對輸出全部進行加密。比如使用該種方法:上表中的四個輸出值0、0、0、1 分別加密為——

——這樣一來,輸出的四個值分別對應為四個不同的密文。因此,在此環境下, 無法通過上述推斷來反推出A的輸入值是0 還是1。但是,這種方法使得輸出加密值的個數從二變成了四。通信複雜度會增大。
此外,非交互式的不經意傳輸協議也值得研究。
總結
上述方法首先不考慮需要實現MACI 匿名化的兩個目標,即在明文下設計一個算法,讓O能夠正確判斷是否執行用戶A的請求。基於此,再將所設計的算法轉化成邏輯電路。再將邏輯電路轉化成混淆電路。需要注意的是,邏輯電路在每一個區塊鏈的epoch 中是固定的且能夠從區塊鏈中直接獲取的。用戶A獲取該epoch 的邏輯電路,利用相應工具將邏輯電路轉化成混淆電路。同時,用戶A將每一個混淆電路的輸入進行加密,並將加密好的信息發送給O。此時,O由於不知道加密後的輸入對應的明文是什麼,O也就不知道用戶A具體的輸入是什麼了,這樣就實現了匿名化的第一個性質。
進而,使用不經意傳輸是實現第二個目的的方法。通過不經意傳輸,用戶A並不知道O具體採用了哪些加密值進行進一步的輸入,因此用戶A無法推斷出deactivate[] 數組中的其他元素信息。同時,由於O通過不經意傳輸獲得了足夠的有效輸入,因此O將這些有效輸入輸入到被加密的混淆電路中,最終能夠得到正確的輸出,該輸出和明文下執行第一節的算法所得到的輸出是相同的。因此,O就能夠根據輸出來判斷是否要執行用戶A的請求。
最終,O將上述所有操作利用零知識證明生成操作的proof。區塊鏈對proof 進行驗證,驗證通過後,區塊鏈將根據deactivate[] 數組中的元素和registry 數組中的元素來更新registry 數組並結束epoch 和開啟下一個epoch。


