原文作者:Steven Wang
“What I cannot create, I do not understand.”
-Richard Feynman
前言
你左擁右抱著Stable Diffusion 和MidJourney 創造美輪美奐的圖片。
你熟練使用著ChatGPT 和LLaMa 創造辭緻雅贍的文字。
你來回切換著MuseNet 和MuseGAN 創造高山流水的音樂。
毋庸置疑,人類最獨特的能力就是創造,但在科技日新月異發展的今天,我們通過創建機器來創造!機器可以給定風格繪製原創藝術品(draw),可以編寫一長篇連貫文章(write),可以創作悅耳的音樂(compose),還可以為複雜遊戲制定獲勝策略(play)。這個科技就是生成式人工智能(Generative Artificial Intelligence, GenAI),現在只是GenAI 革命的開始,現在是學習GenAI 的最佳時機。
1.生成和判別模型
GenAI 是一個buzzword,其背後本質是生成模型(generative model),它是機器學習的一個分支,目標是訓練模型以生成與給定數據集相似的新數據。
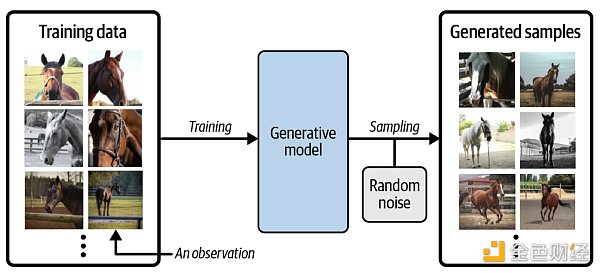
假設我們有一個馬的數據集。首先,我們可以在此數據集上訓練生成模型,以捕獲控制馬圖像中像素之間複雜關係的規則。然後,從此模型中進行採樣,以創建原始數據集中不存在的但是逼真的馬圖像,過程如下圖所示。
為了真正理解生成模型的目標和重要性,將其與判別模型(discriminative model) 進行比較是必要的。其實機器學習里大多數的問題都是由判別模型解決的,看以下例子。
假設我們有一個繪畫數據集,一些是梵高畫的,一些是其他藝術家畫的。有了足夠的數據,我們就可以訓練一個判別模型來預測一幅給定的畫是否由梵高所作,過程如下圖所示。
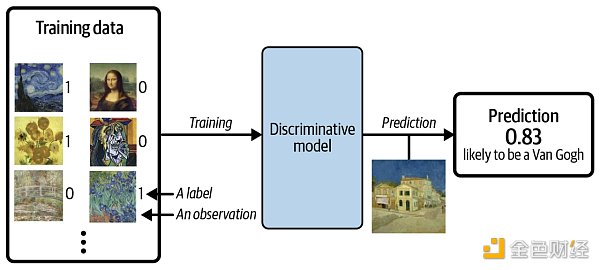
當使用判別模型時,訓練集中每個示例都有一個標籤(label),對於以上二分類問題,通常梵高的畫的標籤為1 ,非梵高的畫的標籤為0 。上圖中模型最後預測的概率是0.83 ,那麼它很有可能是由梵高所作。和判別模型不同的是,生成模型不需要示例裡含有標籤,因為它的目標是生成新數據,而不是給數據預測標籤。
例子看完,讓我們用數學符號來精准定義生成模型和判別模型:
-
判別模型對P(y|x) 建模,給定特徵x 來估計標籤y 的條件概率。
-
生成模型對P(x) 建模,直接估計特徵x 的概率,從這個概率分佈中採樣即可生成新的特徵。
需要注意的是,即使我們能夠建立一個完美來識別梵高的畫的判別模型,它仍然不知道如何創作一幅看起來像梵高的畫,它只能輸出一個概率,即圖像是否來自梵高之手的可能性。由此可見,生成模型比判別模型要困難很多。
2.生成模型的框架
了解生成模型框架之前,讓我們先玩一個遊戲。假設下圖的點是由某種規則產生,我們稱該規則為Pdata,現在讓你生成一個不同的x = (x 1, x 2) 使得這個點看起來是由相同的規則 Pdata 產生的。
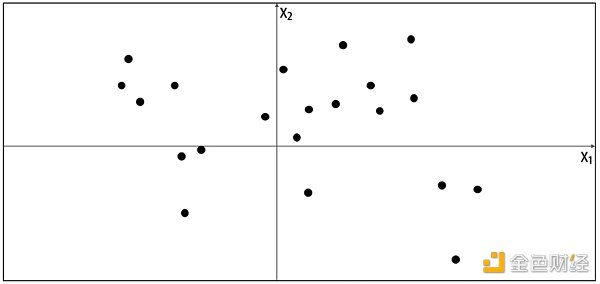
你會如何生成這個點?你可能利用已給的點在腦海裡產生一個模型Pmodel,而這個模型占的位置上都可能生成你想要的點。由此可知,模型Pmodel 就是Pdata 的估計。那麼一個最簡單的模型Pmodel 如下圖的橙色方框,點只可能生成於方框內,而不可能生成於方框外。
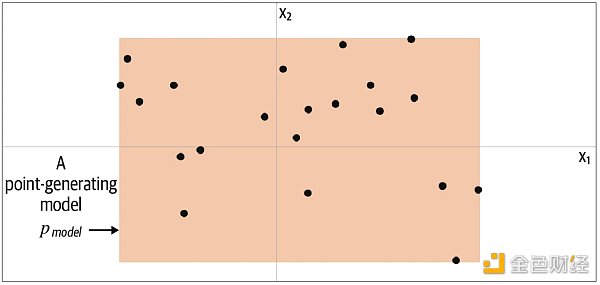
要生成新的點,我們可以從方框內隨機選一個點,更嚴謹地說,從模型 Pmodel 分佈中採樣(sampling)。這就是一個極簡的生成模型。你從訓練數據(黑點) 中創建一個模型(橙框),然後你可以從模型中採樣,希望生成出來的點和訓練集中的點看起來相似。
現在我們可以正式提出生成學習的框架了。

現在讓我們揭示真實的數據生成分佈 Pdata,並了解如何應用以上框架於此示例。從下圖中我們可以看到,數據生成規則 Pdata 是點只是在陸地上均勻分佈,而不會出現在海洋中。
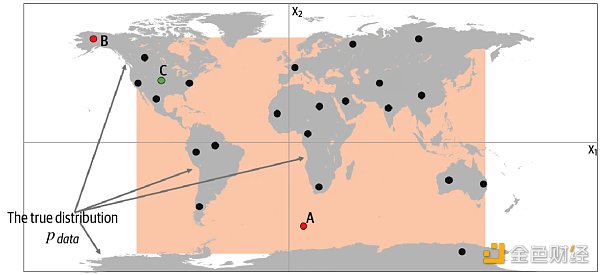
很明顯,我們的模型 Pmodel 是規則 Pdata 的一個簡化。通過檢查上圖的A、B 和C 點可以幫助我們理解模型 Pmodel 是否成功模仿了規則 Pdata。
-
點A 不符合規則 Pdata,因為它出現在海裡,但可能由模型 Pmodel 生成,因為它出現在橙框之內。
-
點B 不可能由模型 Pmodel 生成,因為它出現在橙框之外,但符合規則 Pdata,因為它出現在陸地上。
-
點C 由模型 Pmodel 生成,而又符合規則 Pdata。
這個例子展示了生成建模背後的基本概念,雖然現實中用生成模型要復雜很多,但其基本框架是相同的。
3.第一個生成模型
假設你是一家公司的首席時尚官Chief Fashion Officer (CFO),你的職責是創造新的時髦的衣服。今年你收到50 個關於時尚搭配的數據集(如下圖),而你需要創造10 個新的時尚搭配。

雖然你是首席時尚官,但是你也是一個數據科學家,因此你決定用生成模型來解決此問題。看完上面50 張圖片,你決定用五個特徵,配件類型(accessies type)、服裝顏色(clothing color)、服裝類型(clothing type)、頭髮顏色(hair color) 和頭髮類型(hair type),來描述時尚搭配。
前10 個圖像數據特徵如下。
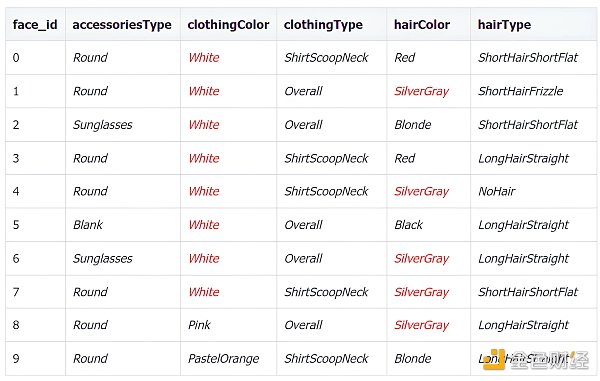
每個特徵也有不同數目的特徵值:
-
3 種配件類型(accessies type):
Blank, Round, Sunglasses
-
8 種服裝顏色(clothing color):
Black, Blue 01, Gray 01, PastelGreen, PastelOrange, Pink, Red, White
-
4 種服裝類型(clothing type):
Hoodie, Overall, ShirtScoopNeck, ShirtVNeck
-
6 種頭髮顏色(hair color) :
Black, Blonde, Brown, PastelPink, Red, SilverGray
-
7 種頭髮類型(hair type):
NoHair, LongHairBun, LongHairCurly, LongHairStraight, ShortHairShortWaved, ShortHairShortFlat, ShortHairFrizzle
這樣有3 * 8 * 4 * 6 * 7 = 4032 種特徵組合,所以可以想成樣本空間裡麵包含著4032 個點。從給出的50 個數據點可以看出,Pdata 對於不同特徵會偏好某些特徵值。從上表看出圖像中白色服裝顏色和銀灰色頭髮顏色就比較多。由於我們不知道真實的 Pdata,我們只能通過這50 個數據來建一個 Pmodel ,使其能夠和 Pdata 相近。
3.1 極簡模型
一個最簡單的方法就是給4032 個特徵組合中每個點賦予一個概率參數,那麼該模型包含4031 個參數,因為所有概率參數加起來等於1 。現在我們來一個個檢查50 個數據,然後更新該模型的參數(θ 1 ,θ 2 ,…,θ 4031 ),每個參數的表達式為:
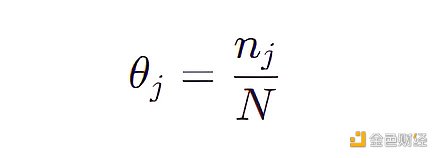
其中N 是觀測數據的個數即50 ,nj 是第j 個特徵組合在50 個數據中出現的個數。
比如(LongHairStraight, Red, Round, ShirtScoopNeck, White) 的特徵組合(稱為組合1) 出現了兩次,那麼
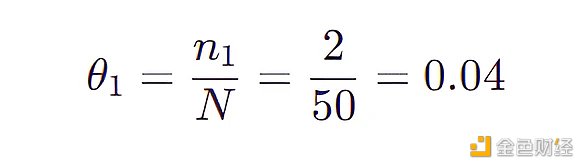
比如(LongHairStraight, Red, Round, ShirtScoopNeck, Blue 01) 的特徵組合(稱為組合2) 沒有出現,那麼
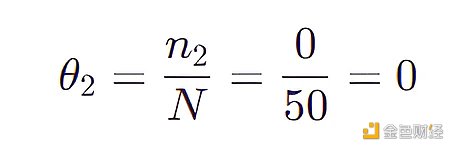
按照上面的規則,我們將4031 個組合都計算出一個θ 值,不難看出有很多 θ 值都是0 ,更糟的是我們不可能生成新的沒見過的圖片( θ = 0 意味著從未觀測到擁有該特徵組合的圖片)。為了解決此問題,只需在分母加上特徵數目的總數d 和在分子加上1 ,該技巧叫做拉普拉斯平滑。
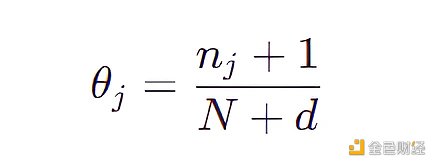
現在,每個組合(包括那些不在原始數據集中的組合) 都有非0 的採樣概率,然而這仍然不是一個令人滿意的生成模型,因為不在原始數據集中的點的概率是一個常數。如果我們嘗試使用這樣的模型來生成梵高的畫,那麼它會以相同概率來操作一下兩種畫:
-
梵高原作的複制畫(不在原始數據集)
-
隨機像素拼湊的畫(不在原始數據集)
這顯然不是我們想要的生成模型,我們希望它能從數據中學到一些固有的結構,從而能夠增加樣本空間中它認為更有可能的區域的概率權重,而不是把所有概率權重放在數據集中存在的點上。
3.2 次簡模型
樸素貝葉斯模型(Naive Bayes) 可以將上面特徵組合的次數大大減少,根據其模型假設每個特徵之間都是相互獨立的。回到上面的數據,一個人的頭髮顏色(特徵xj ) 和其衣服顏色(特徵xk ) 沒有聯繫,用數學表達式表示就是:
p(xj | xk) = p(xk)
有了這個假設,我們可以計算出
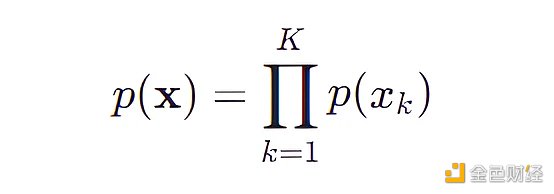
樸素貝葉斯模型將原始問題“對每個特徵組合做概率估計”簡化成對“每個特徵做概率估計”,原來我們需要用4031 ( 3 * 8 * 4 * 6 * 7) 個參數,現在只需要23 ( 3 + 8 + 4 + 6 + 7) 個參數,每個參數的表達式為:
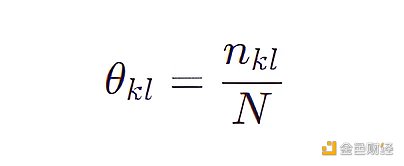
其中N 是觀測數據的個數即50 ,nkl 是第k 個特徵取其下第l 個特徵值的個數。
通過統計50 個數據,下表給出樸素貝葉斯模型的參數值。
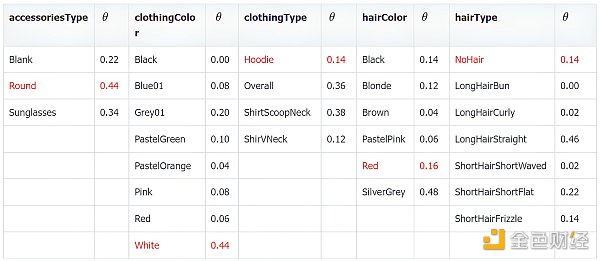
要計算模型生成某數據特徵的概率,只需要連乘上表中的概率, 比如:

以上這個組合沒有出現在原始數據集中,但模型仍然為它分配非零的概率,因此它仍然能夠被模型生成。因此,樸素貝葉斯模型能夠從數據中學習一些結構,並使用它來生成原始數據集中未見過的新示例。下圖是模型生成的10 張新的時尚搭配的圖片。

在此問題中,特徵只有5 個屬於低維數據,樸素貝葉斯模型假設它們相互獨立還算是合理,因此模型生成的結果還不錯,下面來看一個模型崩塌的例子。
4. 生成模型的難點
4.1 高維數據
作為首席時尚官,你成功用樸素貝葉斯生成了10 套全新的時尚搭配,你信心爆棚了,覺得自己的模型無敵,直到遇到下面這套數據集。

該數據集不再是用五個特徵來表示了,而是由32* 32 = 1024 個像素來表示,每個像素值可以去0 到255 中的一個, 0 表示白, 255 表示黑。下表列出前10 張圖像像素1 到5 的值。
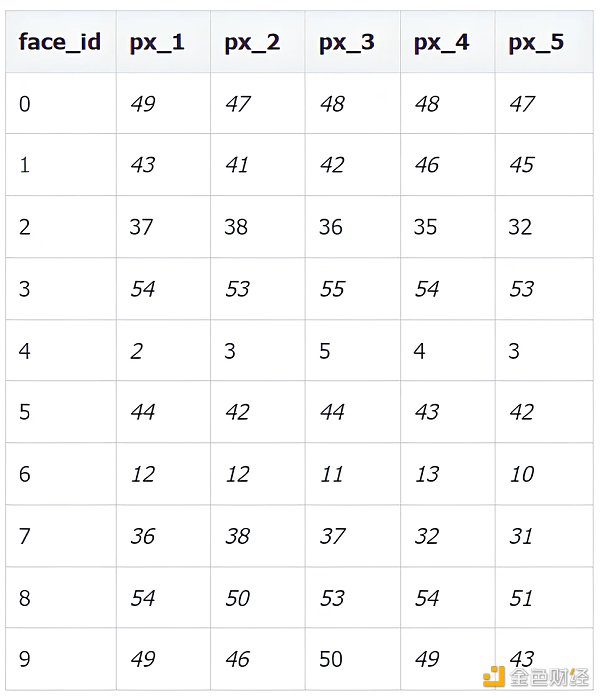
用同樣的模型生成10 套全新的時尚搭配,下面是模型生成的結果,每張醜得都很類似,而且無法區分不同的特徵,為什麼會這樣呢?

首先,由於樸素貝葉斯模型是獨立採樣像素,但是相鄰像素之間其實非常相似。對於衣服,其實像素應該大致相同,但是模型隨機採樣,因此得到上圖中的衣服都是五顏六色的。其次,高維樣本空間中的可能性太多,其中只有一小部分是可識別的。如果樸素貝葉斯模型直接處理這種高度相關的像素值,那麼它找到令人滿意的值組合的機會非常小。
綜上所述,對於低維度而且特徵低相關的樣本空間,樸素貝葉斯效果通過獨立採樣的產生的效果很好;但對於高維度而且特徵高相關的樣本空間,通過獨立採樣像素來找到有效人臉幾乎是不可能的。
這個例子強調了生成模型要想成功必須克服的兩個難點:
-
模型如何處理高維特徵之間的條件依賴關係?
-
模型如何從高維樣本空間中找到滿足條件的極小比例觀察結果?
生成模型要想在高維度而且特徵高相關的樣本空間中成功,必須要利用深度學習模型。我們需要一個可以從數據中推斷出相關結構的模型,而不是被告知要提前做出哪些假設。深度學習可以在低維空間中形成自己的特徵,而這就是表徵學習(representation learning) 的一種形式。
4.2 表徵學習
表徵學習就是學習高維數據的表示的含義。
假設你去見一個從未見過面的網友,到達相約地點人很多根本找不到她,你打電話給她描述你的樣子。相信你不會說你圖像中像素1 的顏色是黑,像素2 的顏色是淡黑,像素3 的顏色是灰等等。相反你會認為網友會對普通人的外貌有一個大概的了解,然後給予這個了解再描述像素組的特徵,比如,你有一頭烏黑亮麗的短髮,戴著一雙金光閃閃的眼鏡等等。通常不超過10 個這樣的描述,網友就可以從腦海中生成你的圖像,該圖像可能很粗糙,但不妨礙網友從幾百個人中找到你,即便她從來沒有見過你。
這個就是表徵學習背後的核心思想,不嘗試直接對高維樣本空間(high-dimensional sample space) 進行建模,而是使用一些低維潛在空間(low-dimensional latent space) 來描述訓練集中的每個觀察結果,然後學習一個映射函數(mapping function),該函數可以獲取潛在空間中的一個點並將其映射到原始樣本空間。換句話說,潛在空間中的每個點都表示著高維數據的特徵。
上面的話如果不好理解,請看下圖由一些灰度罐子圖像組成的訓練集。
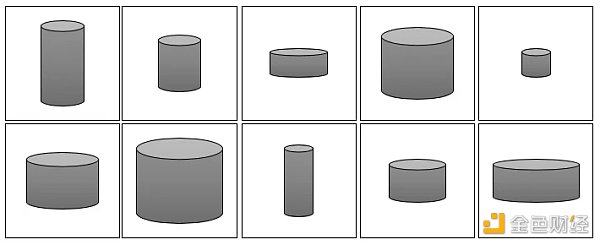
不難看出,這些罐子可以僅用兩個特徵來描述:高度和寬度。因此我們可以圖像的高維像素空間轉換成二維潛在空間,如下圖所示。這樣我們可以從潛在空間採樣(藍點),然後通過映射函數f 將其轉換成圖像。
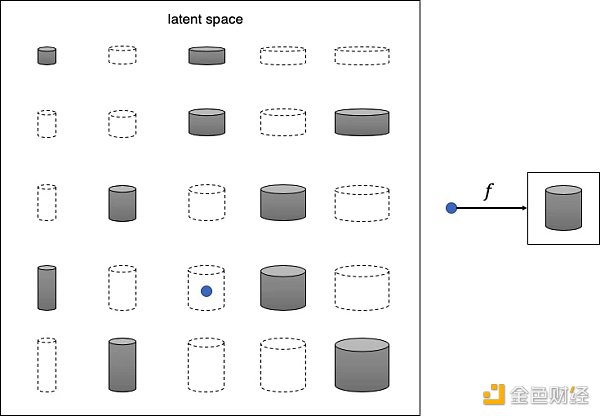
認識到原始數據集可以用更簡單的潛在空間來表示這件事情對於機器來說並不容易,首先機器需要確定高度和寬度是最能描述該數據集的兩個潛在空間維度,然後學習映射函數f 可以在這個空間中取一個點並將其映射到灰度罐圖。深度學習使我們能夠訓練機器,使其無需人類指導即可找到這些複雜的關係。
5. 生成模型的分類
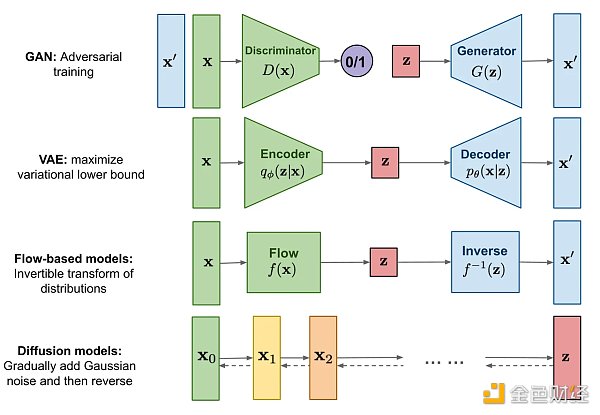
所有類型的生成模型最終都旨在解決相同任務,但它們對密度函數的建模方法都略有不同, 一般來說有以下兩類:
-
對密度函數顯式建模(explicitly modeling),
但以某種方式約束模型,以便計算密度函數,比如標準化流模型(normalizing FLOW model)
但是對密度函數做逼近,比如變分自動編碼器(variational autoencoder, VAE) 和擴散模型(diffusion model)
-
對密度函數隱式建模(implicitly modeling),通過直接生成數據的隨機過程。比如生成對抗網絡(generative adversarial network, GAN)
總結
生成式人工智能(GenAI) 是一種可用於創建新的內容和想法(包括文字、圖像、視頻和音樂) 的人工智能。與所有人工智能一樣,GenAI 是由深度學習模型基於大量數據進行預訓練的超大型模型,通常被稱為根基模型(foundation model, FM)。有了GenAI,我們能畫出更炫酷的圖像,寫出更優美的文字,譜出更動人的音樂,但第一步需要我們去了解GenAI 怎麼創造新的東西,正如文頭Richard Feynman 所說的“我不會明白我無法創造的東西”。