作者:Vitalik Buterin;編譯:布嚕說
在The Three Transitions 這篇文章中,以太坊創始人Vitalik Buterin 明確地闡述了有關「主網(下文簡稱L1)+ 第2 層跨鏈(下文簡稱cross-L2)支持」「錢包安全」和「隱私」作為生態系統堆棧必要功能的重要價值,它們不該只是一些附加的組件,由單獨的錢包提供相關的功能。
而本篇文章,Vitalik Buterin 指出,將重點探討一個關鍵的技術問題:如何能夠更容易地從L2 讀取L1 的數據;或者從L1 讀取L2 的數據;或者如何更容易地從一個L2 讀取另一個L2 的數據。
Vitalik Buterin 指出,解決上述問題的關鍵在於,如何實現資產與密鑰庫的分離架構。這個技術在擴容以外的領域也有非常有價值的用例,比如L1 和L2 之間資產的移動互通。
這樣做的目標是什麼?
一旦L2 成為主流,用戶將能夠在多個L2 上擁有資產,也可能在L1 上擁有資產。
一旦智能合約錢包成為主流,現在常見的「密鑰」將不再被使用。
而一旦這兩件事情同時發生,用戶就會需要一種不需要伴隨大量交易的方法,來更換不同賬戶的密鑰。
尤其是,我們需要一種方法來處理那些「反事實設定」的地址(也可以理解成「假設地址」):這是一些尚未以任何方式在鏈上「註冊」的地址,但仍需要接收並安全地持有資產。
事實上,我們都依賴於這種「反事實設定」的地址:當用戶第一次使用以太坊時,用戶可以生成一個ETH 地址,他人可以向這個賬戶支付,而無需在區塊鏈上「註冊」該地址(但會需要支付交易費用,因此需要持有若干ETH)。
對於外部賬戶(EOA)而言,其實所有的地址都是從「反事實設定」的地址開始的。
對於智能合約錢包,「反事實設定」的地址仍然是可能的,這在很大程度上要歸功於CREATE2,它允許您擁有一個ETH 地址,只能由與特定哈希值匹配的智能合約代碼填充。
△ EIP-1014(CREATE2)地址計算算法。
然而,引入智能合約錢包,也帶來了新的挑戰:訪問密鑰可能發生變化。這個變化在於,地址是initcode 的哈希值,只能包含錢包的初始驗證密鑰,而當前的驗證密鑰將存儲在錢包的存儲中,但該存儲記錄不會自動轉移到其他L2 中。
如果一個用戶在許多L2 上都有地址,這時候就只有資產與密鑰存儲分離架構可以幫助用戶更改他們的密鑰了。
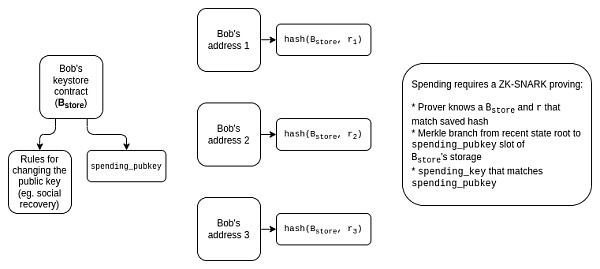
這個分離架構的結構是:每個用戶都有(i)一個「密鑰存儲合約」(在L1 或特定的L2 鏈上),它存儲了所有錢包的驗證密鑰以及更改密鑰的規則,以及(ii)在L1 和許多L2 鏈上的「錢包合約」,它們通過跨鏈讀取來獲取驗證密鑰。

資產與密鑰存儲分離架構有兩種實現方法:
輕量級版本(即僅檢查更新密鑰):每個錢包在本地存儲驗證密鑰,並包含一個可調用的函數來檢查密鑰庫當前狀態的跨鏈證明,並更新本地存儲的驗證密鑰以匹配。在某個L2 上首次使用錢包時,調用該函數從密鑰庫獲取當前的驗證密鑰是必需的。
-
優點:對跨鏈證明的使用較為審慎,不會出現太昂貴的網絡操作費用。所有資產只能通過當前密鑰使用,因此安全性仍然得到保證。
-
缺點:需要更改驗證密鑰,必須在密鑰庫和已初始化的每個錢包上進行鏈上密鑰更改,可能需要消耗很多Gas Fee。
完整版本(即每個交易都檢查):每筆交易都需要一個跨鏈證明,顯示密鑰庫中的當前密鑰。
-
優點:系統複雜性較低,且密鑰庫更新迅速。
-
缺點:單個交易的網絡操作費用較高,不容易與ERC-4337 兼容,ERC-4337 目前尚不支持在驗證期間跨合約讀取可變對象。
什麼是跨鏈證明?
為了展示跨鏈證明的複雜性,我們選取了一種最複雜的應用場景作為展示解釋這個技術原理,這個複雜的應用場景如下:密鑰存儲在一個L2 上,而錢包在另一個L2 上。如果錢包上的密鑰庫在L1 上,那麼只需要此設計的一半。
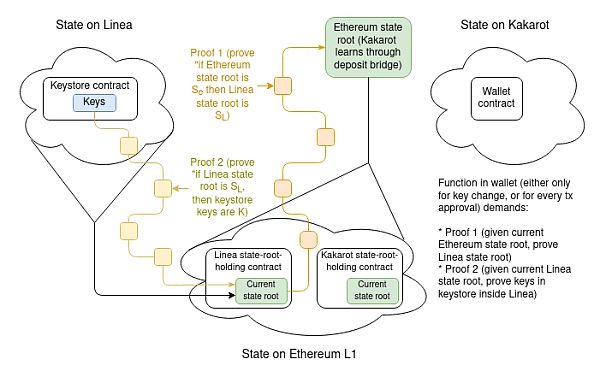
假設密鑰庫在Linea 上,錢包在Kakarot 上。錢包密鑰的完整證明過程則需要包括:
-
證明當前Linea 狀態根的證明,給定Kakarot 知道的當前以太坊狀態根。
-
證明密鑰庫中當前密鑰的證明,給定當前Linea 狀態根。
這裡有兩個主要的棘手的實現問題:「需要使用什麼樣的證據?(是默克爾證明嗎?還是別的什麼?)」以及「L2 如何學習最近的L1 狀態根?」或者,「L1如何學習L2 的狀態根?」
那麼,在這兩種情況下,一方發生某事件後,到另一方能夠提供證明之間,會有多長的延遲時間?
我們可以使用哪些證明方案?
主要有五種方法可供選擇:
-
Merkle 證明
-
通用ZK-SNARKs
-
特殊目的證明(例如,使用KZG)
-
Verkle 證明,介於KZG 和ZK-SNARKs 之間,既考慮基礎設施工作量又考慮成本
-
沒有證明,依賴直接狀態讀取
就所需的基礎設施工作和用戶成本而言,大致可將它們進行如下排列比較:
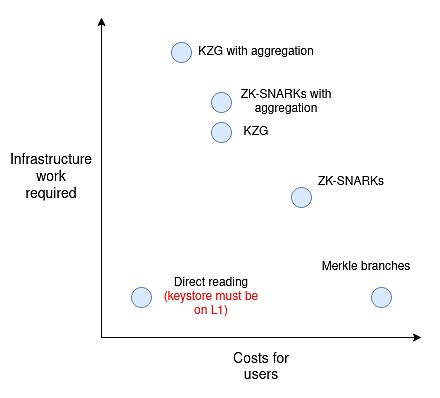
「聚合」是指將每個區塊中用戶提供的所有證明聚合成一個大的元證明,將它們合併在一起。這對於SNARKs 和KZG 是可行的,但對於Merkle 分支來說不行。
事實上,只有當方案擁有大量用戶時,「聚合」才能體現價值。
Merkle 證明是如何工作的?
這個問題很簡單,可以直接按照上一節的圖表。每個「證明」(假設是將一個L2 證明為另一個L2 ,這是難度最大的一種應用場景)將包括:
一個Merkle 分支,證明了持有L2 鍵庫的狀態根,根據L2 所知道的以太坊的最新狀態根。持有L2 鍵庫的狀態根存儲在已知地址(代表L2 的L1 合約)的已知存儲槽中,因此可以將路徑硬編碼。
一個Merkle 分支,證明了當前的驗證密鑰,根據持有L2 鍵庫的狀態根。同樣,驗證密鑰存儲在已知地址的已知存儲槽中,因此路徑可以硬編碼。
然而,以太坊的狀態證明很複雜,但是有一些庫可以用來驗證它們,如果使用這些庫,這個機制並不太複雜。
不過,更大的挑戰是成本問題。 Merkle 證明很長,而Patricia 樹比必要的就是長3.9 倍——遠遠高於目前每筆交易2.1萬個Gas Fee 的基本價格。
但是,如果在L2 上驗證證明,則差異會變得更糟。 L2 內部的計算很便宜,因為計算是在鏈下完成的,並且是在節點大量少於L1 的生態系統裡完成。
我們可以通過查看L1 Gas Fee 成本和L2 Gas Fee 成本之間的比較來計算這意味著什麼:
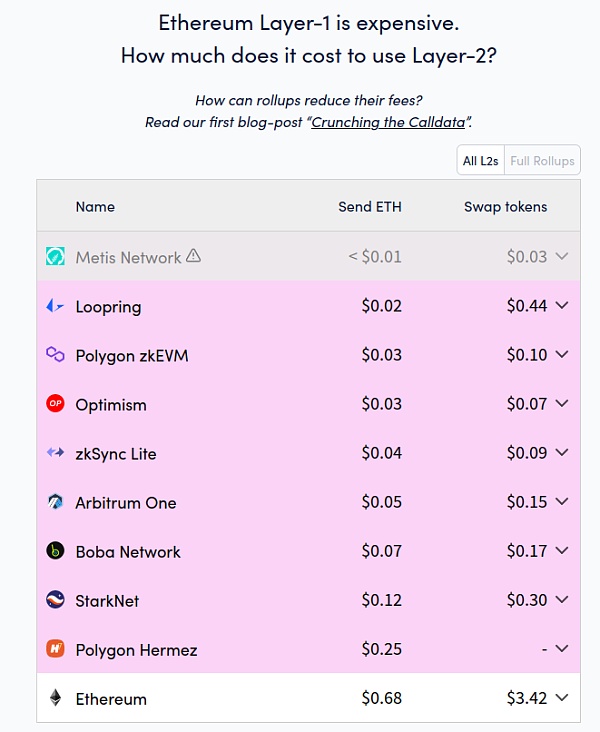
當下,如果是較為簡單的發送操作,L1 網絡上的成本大約是L2 的15~25 倍,而Token 交換的成本則大約是L2 的20~50 倍。
簡單的發送操作,數據量較大;而交換操作對於算力的要求更高,因此,交換操作是一個更好的基準來近似L1 計算與L2 計算的成本。
綜合考慮以上情況,如果我們假設L1 計算成本和L2 計算成本之間的成本比為30 倍,這似乎意味著將Merkle 證明放在L2 上的成本可能相當於大約五十個常規交易。
當然,使用二進制Merkle 樹可以減少成本約為4 倍,但即使如此,在大多數情況下,成本仍然會過高,而且如果我們願意放棄與以太坊當前的六進制狀態樹的兼容性,可能還會尋求更好的選擇。
ZK-SNARK 證明是如何工作的?
從概念上講,ZK-SNARK 的使用也很容易理解:您只需將上圖中的Merkle 證明替換為證明這些Merkle 證明存在的ZK-SNARK。一個ZK-SNARK 的計算量約為400,000 Gas Fee,約400 字節;一個基本事務需要21,000 個Gas Fee 和100 個字節。
因此,從計算角度看,ZK-SNARK 的成本是現在基本交易成本的19 倍;從數據角度看,ZK-SNARK 的成本是現在基本交易成本的4 倍,是未來基本交易成本的16 倍。
這些數字與Merkle 證明相比有了巨大的改進,但仍然相當昂貴。有兩種方法可以改善這種情況:(i) 特殊用途的KZG 證明,或(ii) 聚合,類似於ERC-4337 聚合。
特殊用途的KZG 證明如何工作?
首先,回顧一下KZG 承諾的工作原理:
[D_1 …D_n] 表示一組數據,通過這組數據導出多項式KZG 證明。
具體來說,多項式P,其中P(w) = D_1,P(w²) = D_2 …P(wⁿ) = D_n. w 這裡是「統一根」,對於某些評估域大小N,wN = 1的值(這一切都是在有限域中完成的)。
為了「提交」到P,我們創建一個橢圓曲線點com(P) = P₀ * G + P₁ * S₁ + … + Pk * Sk。這裡:
G 是曲線的生成器點
Pi 是多項式P 的第i 次係數
Si 是可信設置中的第i 個點
而為了證明P(z) = a,我們創建一個商多項式Q = (P – a) / (X – z),並創建一個承諾com(Q)。只有當P(z) 實際上等於a 時,才有可能創建這樣的多項式。
為了驗證證明,我們通過對證明com(Q) 和多項式承諾com(P) 進行橢圓曲線檢查來檢查方程Q * (X – z) = P – a:我們檢查e(com(Q), com(X – z)) ? = e(com(P) – com(a), com(1))
還需要了解的一些關鍵屬性包括:
證明只是com(Q) 值,即48 個字節
com(P₁) + com(P₂) = com(P₁ + P₂)
這也意味著您可以將值「編輯」為現有合約。
假設我們知道D_i 當前是a,我們希望將其設置為b,並且對D 的現有承諾是com(P)。承諾“P,但P(wⁱ) = b,並且沒有其他評估更改”,然後我們設置com(new_P) = com(P) + (ba) * com(Li),其中Li 是「拉格朗日多項式」,在wⁱ 處等於1,在其他wj 點處等於0。
為了有效地執行這些更新,每個客戶端都可以預先計算和存儲對拉格朗日多項式(com(Li)) 的所有N 個承諾。在鏈上合約中,存儲所有N 個承諾可能太多了,所以你可以對com(L_i)值集做出KZG 承諾,所以每當有人需要更新鏈上的樹時,他們可以簡單地向適當的com(L_i) 提供其正確性的證明。
因此,有一個結構可以繼續將值添加到不斷增長的列表的末尾,但有一定的大小限制。然後,使用這個結構作為數據結構(i)對每個L2 上的密鑰列表的承諾,存儲在該L2 上並鏡像到L1,以及(ii)對L2 密鑰承諾列表的承諾,存儲在以太坊L1 上並鏡像到每個L2。
保持承諾更新可以成為核心L2 邏輯的一部分,也可以通過存款和撤回橋接實現,而無需更改L2 核心協議。
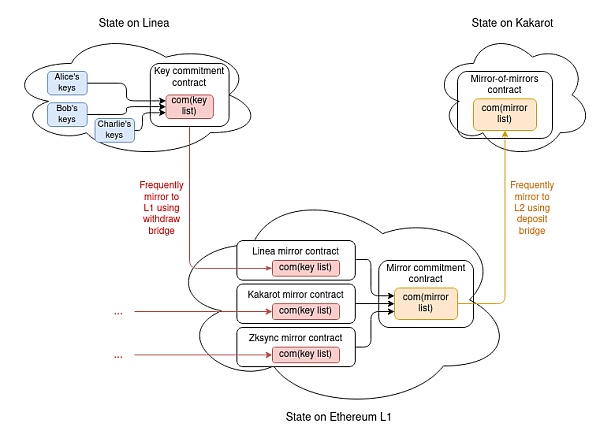
一份完整的證明所需的內容如下:
-
存放L2 上密鑰庫的最新com(密鑰列表)。
-
將com(密鑰列表)作為com(鏡像列表)中的值的KZG 證明,com(鏡像列表)是所有密鑰列表承諾的列表。
-
將用戶的密鑰在com(密鑰列表)中進行KZG 證明。
事實上,上述兩個KZG 證明可以合併為一個,總大小只有100 字節。
請注意一個細節:由於密鑰列表是一個列表,而不是像狀態那樣的鍵/值映射,密鑰列表必須按順序分配位置。密鑰承諾合約將包含其自己的內部註冊表,將每個密鑰庫映射到一個ID,並且對於每個密鑰,它將存儲hash(key,密鑰庫的地址)而不僅僅是key,以明確地告知其他L2 關於特定條目所指的密鑰庫。
這種技術的優點是在L2 上性能非常好。比ZK-SNARK 短約4 倍,比Merkle 證明短得多。計算成本大約為119,000 Gas Fee。
在L1 上,算力比數據更重要,因此KZG 比Merkle 證明要稍微昂貴一些。
Verkle 樹如何工作?
Verkle 樹本質上涉及將KZG 承諾堆疊在一起:要存儲2⁴⁸ 值,可以對2²⁴ 值列表做出KZG 承諾,每個值本身都是KZG 對2²⁴ 值的承諾。
Verkle 樹被考慮用於以太坊狀態樹,因為Verkle 樹可以用來保存鍵值映射。
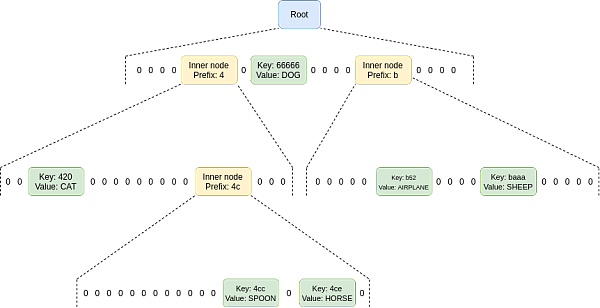
Verkle 樹中的證明比KZG 證明更長,它們可能有幾百個字節長。
實際上,Verkle 樹應該被認為是像Merkle 樹,但如果沒有SNARKing 更可行,但SNARKing 被證明有更低的證明成本。
Verkle 樹的最大優點是可以協調數據結構:因此可以直接用於L1 或L2,沒有疊加結構,並且對L1 和L2 使用完全相同的機制。
一旦量子計算機成為一個問題,或者一旦證明Merkle 分支變得足夠高效,Verkle 樹就有了更多地用武之地。
聚合
如果N 個用戶做了N 筆交易,需要證明N 個跨鏈索賠,我們可以通過聚合這些證明來節省大量的Gas Fee,這可能意味著:
-
一個N 個Merkle 分支的ZK-SNARK 證明
-
一個KZG 多重證明
-
一個Verkle 多重證明(或一個多重證明的ZK-SNARK)
在所有這三種情況下,每個證明只需花費幾十萬Gas Fee。
開發者需要在每個L2 上為該L2 的用戶製作一個這樣的證明;因此,為了使這個證明有用,整個計劃需要有足夠的使用量,以至於在多個主要L2 的同一區塊內經常有至少幾個交易。
如果使用ZK-SNARKs,每個用戶可能需要花費幾千個L2 Gas Fee。如果使用KZG 多重證明,驗證者需要為該區塊內使用的每個持有鑰匙庫的L2 增加48 個Gas Fee。
不過,這些成本比不聚合的成本要低得多,後者不可避免地涉及到每個用戶超過10000 個L1 Gas Fee 和數十萬個L2 Gas Fee。
對於Verkle 樹,用戶可以直接使用Verkle 多證明,每個用戶增加大約100~200 字節,或者你可以做一個Verkle 多證明的ZK-SNARK,它的成本與Merkle 分支的ZK-SNARK 相似,但證明起來明顯便宜。
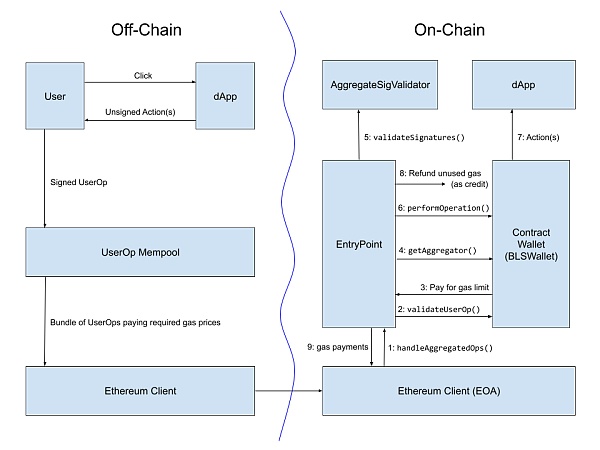
從實施的角度來看,讓捆綁者通過ERC-4337 賬戶抽象標準聚合跨鏈證明可能是最好的。 ERC-4337 已經有一個機制,讓構建者以自定義的方式聚合User Operations 的部分。甚至有一個針對BLS 簽名聚合的實現,這可以將L2 的Gas Fee 降低1.5 倍到3 倍。
直接讀取狀態
最後一種可能,也是只適用於L2 讀L1(而不是L1 讀L2)的一種可能,就是修改L2,讓它們直接對L1 的合約進行靜態調用。
這可以通過一個操作碼或預編譯來實現,它允許調用L1,你提供目標地址、氣體和calldata,然後它返回輸出,儘管由於這些調用是靜態調用,它們實際上不能改變任何L1 狀態。 L2 必須知道L1 的情況才能處理存款,所以沒有什麼根本性的東西可以阻止這種東西的實現;這主要是一個技術實現上的挑戰。
請注意,如果密鑰庫在L1 上,並且L2 整合了L1 的靜態調用功能,那麼就根本不需要證明。
但是,如果L2 沒有整合L1 靜態調用,或者如果密鑰庫在L2 上,那麼就需要證明了。
L2 如何學習最近的以太坊狀態根?
上述所有方案都要求L2 訪問最近的L1 狀態根或整個最近的L1 狀態。
事實上,如果L2 具有存入功能,那麼您可以按原樣使用該L2 將L1 狀態根移動到L2 上的合約中:只需讓L1 上的合約調用BLOCKHASH 操作碼,並將其作為資產存入的消息傳遞給L2。可以在L2 端接收完整的塊標頭,並提取其狀態根。
但是,每個L2 最好都有明確的方式來直接訪問完整的最新L1 狀態或最近的L1 狀態根。
優化L2 接收最新L1 狀態根的方式的主要挑戰是同時實現安全性和低延遲:
-
如果L2 緩慢實現直接讀取L1 功能,只讀取最終的L1 狀態根,那麼延遲通常為15 分鐘,但在一些極端情況下,延遲可能是幾週。
-
L2 絕對可以設計為讀取更新的L1 狀態根,但由於L1 可以恢復(即使具有單插槽終結性,在非活動洩漏期間也會發生恢復),L2 也需要能夠恢復。從軟件工程的角度來看,這在技術上具有挑戰性。
-
如果使用橋將L1 狀態根引入L2,那麼資產更新需要花費很長的時間,在最好的情況下,不斷有用戶支付更新費用,並使系統為其他人保持最新狀態。
-
不過,「預言機」(Oracles)在這裡不是一個可接受的解決方案:錢包密鑰管理是一個非常安全的關鍵低級功能,因此它最多應該依賴於幾個非常簡單的、無需加密信任的低級基礎設施。
此外,在相反的方向上(L1 讀取L2):
-
在Optimistic Rollup 中,由於欺詐證明延遲,州根需要一周才能達到L1。在ZK 匯總中,由於驗證時間和經濟限制的結合,現在需要幾個小時,儘管未來的技術將減少這種情況。
-
預確認(來自測序儀、證明者等)不是L1 讀數L2 的可接受解決方案。錢包管理是一個非常安全關鍵的低級功能,因此L2 到L1 的通信安全級別必須是絕對的高。 L1 應信任的唯一狀態根是已被L2 在L1 上的狀態根持有合約接受為最終狀態根。
對於許多DeFi 用例來說,其中一些用於無信任跨鏈操作的速度慢得令人無法接受。然而,對於更新錢包密鑰的用例,更長的延遲更容易接受——因為不是延遲交易,是延遲密鑰更改。
用戶只需要將舊密鑰保留更長時間即可。如果用戶因為密鑰被盜而更改密鑰,那麼確實有很長一段時間的漏洞,但可以緩解,例如。通過具有凍結功能的錢包。
最終,最好的延遲最小化解決方案是讓L2 以最佳方式實現對L1 狀態根的直接讀取,其中每個L2 塊(或狀態根計算日誌)包含一個指向最新L1 塊的指針,因此如果L1 恢復,L2 也可以恢復。密鑰庫合約應放置在主網上或ZK-rollup 的L2 上,以便可以快速提交到L1。
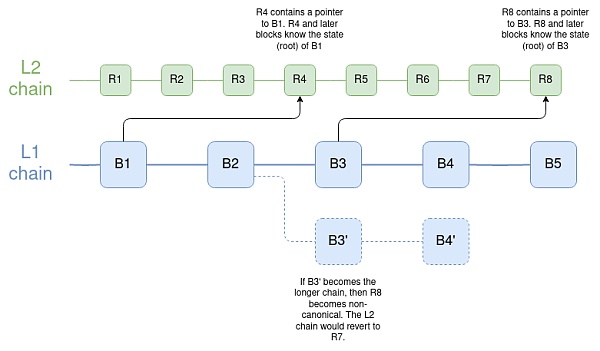
另一個鏈需要多少與以太坊有多少連接,才能持有密鑰庫存儲在以太坊或L2 的錢包?
令人驚訝的是,沒有那麼多。實際上,它甚至不需要是一個Rollup。
如果它是一個L3,或者是一個validium,那麼在那裡存放錢包也是可以的,只要用戶在L1 或ZK-rollup 上存放密鑰存儲,確實需要能夠直接訪問以太坊的狀態根,以及願意在以太坊重構時,在以太坊硬分叉時進行硬分叉。
基於ZK 橋的方案有吸引人的技術特性,但它們有一個關鍵的弱點,即它們對51% 攻擊或硬分叉不健全。
保護隱私
理想情況下,用戶還希望保護隱私。如果一個用戶有許多由同一個密鑰庫管理的錢包,那麼他們希望確保:
-
不讓公眾知道這些錢包都是相互連接的。
-
社交恢復監護人不會了解他們所監護的地址是什麼。
但這就產生了一下問題:
-
我們不能直接使用Merkle 證明,因為它們不能保護隱私。
-
如果我們使用KZG 或SNARKs,那麼證明需要提供驗證密鑰的盲版,而不洩露驗證密鑰的位置。
-
如果我們使用聚合,那麼聚合器就不應該以明文的方式了解位置;相反,聚合器應該接收盲證明,並有辦法聚合這些證明。
-
我們不能使用「輕量級版本」(僅在更新密鑰時使用跨鏈證明),因為這會造成隱私洩露:如果許多錢包由於更新程序而同時更新,那麼時間上就會洩露這些錢包可能相關的信息。因此,我們必須使用「完整版本」(對每筆交易進行跨鏈證明)。
對於SNARKs,解決方案在概念上很簡單:默認情況下證明是信息隱藏的,聚合器需要產生遞歸SNARK 來證明SNARKs。
這種方法目前面臨的主要挑戰是:聚合需要聚合器創建一個遞歸的SNARK,速度上相當慢。
對於KZG,我們可以使用非索引揭示KZG 證明的工作。然而,盲證的聚合是一個開放的問題,需要更多的關注。
不過,雖然從L2 內部直接讀取L1 並不能保護隱私,但實現這個直接讀取功能仍然將非常有用——不僅因為可以最大限度地減少延遲,還可以用於其他更多用例。