前段時間在翻譯一本零知識證明技術的書。上個月底基本內容已經翻譯完成。翻譯時間比我預想的長得多。目前正在和作者討論書中的一些筆誤,準備最後的定稿。
anyway,終於有點時間看看新鮮東西。先從Nova算法開始~
Nova算法相關資料
三份資料可以幫助理解Nova算法:
-
Nova論文:https://eprint.iacr.org/2021/370.pdf
-
Nova潛在攻擊和相應修正:https://eprint.iacr.org/2023/969.pdf
-
Nova潛在攻擊的理解總結:https://www.zksecurity.xyz/blog/posts/nova-attack/
本文是上述資料的理解和總結。本文中的一些圖來自於上述資料,在本文中不再一一標註。
從IVC開始
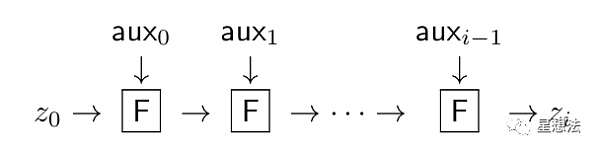
Nova算法是一種針對IVC(增量可驗證計算,Incrementally Verifiable Computation)的新型的零知識證明算法。 IVC,即同一個函數把前一個輸出作為下一個輸入迭代計算。 F函數的迭代計算過程如下圖:
z0是最初的輸入,通過F函數計算生成的結果,作為下一個F函數的輸入。
鬆弛R1CS以及鬆弛承諾R1CS
眾所周知,R1CS是零知識證明技術中電路約束表示形式。鬆弛R1CS(Relaxed R1CS)可以看成是R1CS的擴展形式。在R1CS的基礎上,增加一個標量u以及一個錯誤向量E。鬆弛R1CS的實例用(E, u, x)表示。

鬆弛承諾R1CS在鬆弛R1CS的基礎上,將E以及W向量承諾。鬆弛承諾R1CS的實例用(\bar{E}, u, \bar{W}, x)表示,其中x和u是公開變量。

從R1CS擴展到鬆弛R1CS,是為了折疊方案。注意的是,從鬆弛R1CS的角度看,R1CS是其的一種特例。也就是說,R1CS也是一種“特別“的鬆弛R1CS。
折疊方案(Folding Scheme)
直覺上來說,一個關係R的折疊方案就是將兩個符合關係R的實例“折疊成”一個新的複合關係R的實例。鬆弛R1CS/鬆弛承諾R1CS就能進行類似的折疊。兩者的折疊過程類似。鬆弛承諾R1CS的折疊方案如下:

整個折疊方案由4步組成。第一步,證明者P發送一個交叉項T的承諾\bar{T}給驗證者。第二步,驗證者發送隨機挑戰r給證明者。第三步是證明者和驗證者都需要執行的,承諾的折疊。第四步,證明者獨自執行,將兩個實例的E和W向量進行折疊。
增廣函數F’ (Argumented Function)
折疊方案,折疊的是鬆弛R1CS實例。那這些鬆弛R1CS實例證明的計算是什麼?顯然,這些計算要包括折疊的計算。這些計算不僅僅是IVC計算中的F函數了,也就被稱為增廣函數F’。增廣函數F’的計算主要由兩部分組成:
1/ IVC中的F函數
2/ R1CS實例的折疊計算
理想中的樣子
有了上述的這些理解,可以想像出折疊的過程:
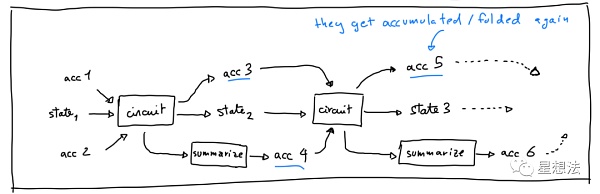
其中,circuit就是增廣函數F’對應的電路。 acc{1,2,3,4,5,6}是鬆弛承諾R1CS實例。 circuit有兩個計算:1/鬆弛承諾R1CS實例的折疊,比如acc1+acc2->acc3。2/計算F函數,將狀態state1變為state2,再從state2變為state3等等。
注意的是,增廣函數F’對應的circuit,本身也是一個R1CS實例,其可以表示成鬆弛R1CS實例。也就是圖中的acc4和acc6。 “summarize”是將鬆弛R1CS實例轉換為鬆弛承諾R1CS實例。
仔細觀察第二個電路的輸入,acc3是折疊後的鬆弛承諾R1CS實例,acc4是證明acc3是正確折疊結果的鬆弛承諾R1CS實例。這兩個實例會進入下一次的折疊,生成acc5。你可以試想一下,如果acc3以及acc4是可滿足的鬆弛承諾R1CS實例,意味著,acc3是由兩個可滿足的鬆弛承諾R1CS實例折疊而來,也就是說,acc1以及acc2是可滿足的鬆弛承諾R1CS實例。這樣的可靠性也就可以一步步“向”前推導,從而也證明了每一次circuit中的F函數計算是正確的。總的來說,就是通過某一個circuit對應的兩個鬆弛承諾R1CS實例的可滿足性,可以證明之前所有的IVC計算是正確的。
真實的樣子
熟悉零知識證明的朋友,都知道多項式承諾方案中經常採用橢圓曲線。 scalar域上對應的多項式的承諾是用橢圓曲線的base域表示。 R1CS電路通常是採用scalar域來表示。仔細看,上圖中的“summarize”的前後涉及到域的轉換。也就是,要將circuit對應的鬆弛承諾R1CS實例進行折疊的話,必須在另外一個電路中去“折疊”。這時,需要引入橢圓曲線循環,兩個或者多個橢圓曲線,其中一個曲線的scalar域,和另外一個曲線的base域相同,巧的是,該曲線的scalar域和之前曲線的base域相同。採用這樣的橢圓曲線循環,可以將“理想中的樣子”實現:
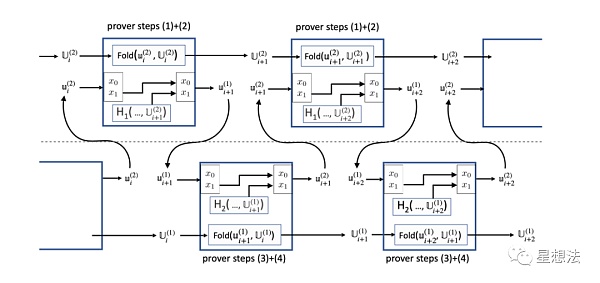
整個折疊過程,拆分成兩個電路進行折疊。上部分可以稱為Circuit 1的折疊,下部分可以稱為Circuit 2的折疊。兩個電路的關係的形式化表示在論文“Nova潛在攻擊和相應修正”的第8頁。 U表示的是折疊後的實例,u表示的是一個R1CS實例對應的鬆弛實例。注意的是,Circuit 1折疊的是Circuit 2對應的鬆弛承諾R1CS實例,而Circuit 2折疊的才是Circuit 1對應的鬆弛承諾R1CS實例。 Circuit 2的主要目的就是折疊Circuit1對應的鬆弛承諾R1CS實例,其電路中的函數計算沒有意義。相反,F函數實現在Circuit 1中。結合“理想中的樣子”,大致可以猜到U{i+2}^2, u{i+2}^1, u{i+2}^2, U{i+2}^1可滿足性是證明的重要部分。
因為“電路”切割成兩部分,並且各自的電路在另外的電路中進行折疊。存在幾個實例之間的綁定問題:u和U實例之間的綁定以及u實例在兩個電路之間傳遞的綁定。為了解決這些綁定問題,在電路中引入了x_0/x_1公開變量,其中x_1指定了和u實例綁定的電路輸出U實例和當前的F函數的輸出(為了簡化電路結構,在圖中未體現)。你想,在電路中引入了U實例的H_1結果的話,如果u實例是可滿足的,x_0/x_1既是真實可靠的,即和U進行了“綁定”。 x_0建立的是輸入的u和U的綁定關係,x_1建立的是輸出的u和U的綁定關係。
舉個例子,u{i+1}^1作為下半部分電路的輸入時,經過Circuit 2,其輸出u{i+1}^2.x0 = u{i+1}^1.x1,這樣,再輸入到上半部分電路時,如果u{i+1}^2可滿足的話,則其的x_0應該等於U_{i+1}^2的H1的結果。這在Circuit 1電路中會進行檢查。這樣,就保證了正確的實例,在兩個電路之間傳遞。
IVC的證明
為了證明IVC在某個迭代正確計算,邏輯上需要證明如下信息:

除了證明四個實例可滿足外,還需要證明兩個x1的綁定關係,示意如下圖:
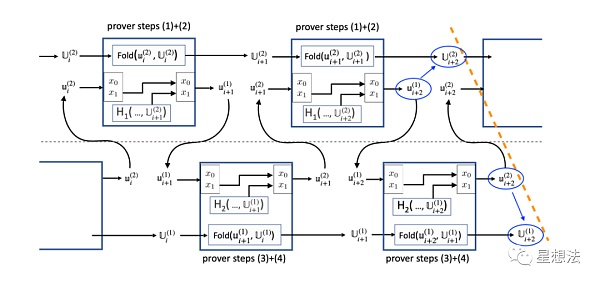
這些信息是否正確,需要額外的證明電路實現。也就是說,IVC計算的證明是該電路的證明。可想而知,如果是很多次迭代的計算,原本需要將這些迭代一個個地在電路中展開,現在只需要對4個電路實例進行可滿足性以及綁定關係的驗證即可。性能提升非常大。
攻擊以及算法修正
看到上面的圖,有個直覺,怎麼感覺上下電路的實例是“割裂“的,沒有什麼綁定性。事實上,攻擊就是這樣構造的。
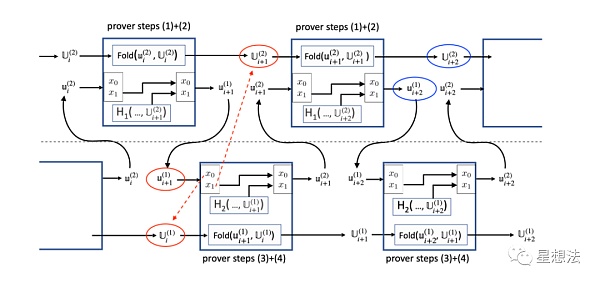
偽造U_i^1和U{i+1}^2,雖然是偽造的,但是是可滿足的實例。偽造u{i+1}^1,修改x_0和x_1和偽造的U實例對應。顯然,u{i+1}^1實例不滿足。雖然它不滿足,但是Circuit 2的電路還是可以滿足的,只是輸出U{i+1}^1實例不滿足而已。成功構造了u{i+1}^2的話,Circuit 1就可以構造出可滿足的u{i+2}^1以及U_{i+2}^2,並且滿足x1的綁定關係。這樣就先構造出了最終偽造證明的一半內容。通過對稱性,可以構造出下面一半的輸出實例。通過兩次構造的結果的“拼接”,可以偽造出IVC計算的證明。
修正後的檢查邏輯如下:
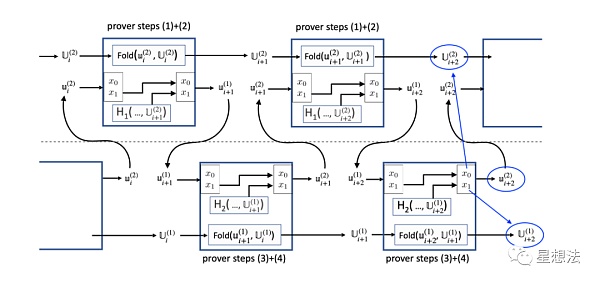
“Nova潛在攻擊和相應修正”論文的第6章給出了詳細的安全性分析。感興趣的小伙伴,可以自行查看原論文。
Nova的基本思想是通過折疊方案折疊電路實例。邏輯比較繞,需要仔細地思考電路折疊過程以及實現電路中的綁定關係。
一個字形容:絕~