文章:@Buidler DAO 作者:@observerdq
Intro
本文是「相看兩不厭:Uniswap 與Curve 的比較研究」系列文章的第一篇,是作者讀了Dan Robinson「Uniswap v3: The Universal AMM」1 一文後延伸出的思考。
目錄
1. Curve V1 公式所建構的思考路徑
2. Uniswap V3 公式所建構的思考路徑
3. 奇妙的擦肩而過- 兩種思維路徑的交點
4. 分道揚鑣- 兩種思考路徑的不同終點
4.1 Curve V1:進一步的動態漸層揉合
4.2 Uni V3:放棄大一統單一公式,自由組合分段函數
5. 結語
一圖總覽
有一個很妙的發現。
2019年Curve V1 在構造AMM 公式時,推演過程中有一個中間形態的公式,而這個公式和一年多後Uniswap V3 的基礎公式恰恰有著相同的結構(前者是後者的一種特殊形態)。
完全不同的思考路徑,出現了數學上的交點,妙哉。
本文將從起點梳理Curve V1 和Uniswap V3 的構造思考過程,兩者在構造過程中數學意義上的擦肩而過,以及是如何地又分道揚鑣通往不同的終點。
1. Curve V1 公式所建構的思考路徑
2018年底Uniswap 的xy = k 橫空出世,是為一場典範革命。但在穩定幣交易對的場景下,缺陷顯著。 Michael 抓住了此切入點,於19年底推出了全新AMM Curve V1 。
新AMM 公式建構過程的基礎之一仍然是xy = k。後續將統一依照Curve V1 白皮書的參數代號,寫為以下公式。
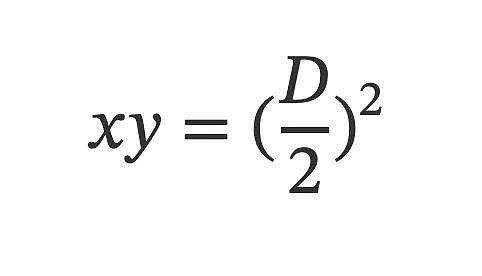
穩定幣交易對的價格多數時候只在1:1 附近很小的區間浮動,只在1:1 單一價格點提供流動性的公式便是x+y = D,這是構造過程的另一基礎。
Michael 希望將兩個基礎公式揉合起來,又或者說在xy = (D/2)² 的基礎之上,引入一些x+y =D 的特性。
於是把兩個基礎公式「雜交」加到了一起,得到了一個揉合公式。
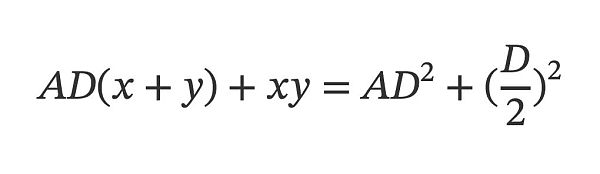
其中x+y=D 的部分,配上了一個A 參數,且額外在等號兩側都乘上了D。乘以D 的原因,是為了讓A 參數去維度化(不論池子內是兩代幣、三代幣亦或更多,同樣的A 值有同樣的效力),這裡不展開,也並非本次討論的重點。
重點在A 參數。先說明一下,Curve V1 白皮書在揉合公式內使用的是希臘字母Chi(長得很像x ),而不是A。為了書寫方便和閱讀體驗,我改用了A ,並不會影響論述。
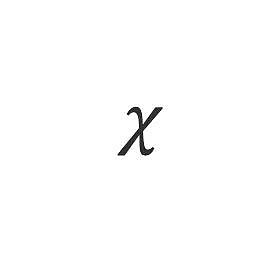
A 參數的作用,或許可以用黑灰白的色條來類比理解,90%灰就很像黑了,而10%灰就更接近白。 A 參數決定了最終的公式產物比較像x+y=D,還是比較像xy=(D/2)²。
從極限A 的數值,可以更好地理解這個揉合的過程。 A = 0,揉合公式就變成了xy=(D/2)²。 A = 無窮大,揉合公式就變成x+y=D了。於是A 在其中,就是一種中間態,A 越大,就越像x+y=D。這種揉合,透過圖形可以更直觀地感受,有興趣可在 desmos² 中玩耍A。
關於Curve V1,講到這裡先停住,請大致記住這個揉合公式。然後我們接著去看Uniswap V3 的情況。
2. Uniswap V3 公式所建構的思考路徑
Uni V1/V2 的xy = k 稱霸江湖後,因「流動性均勻分佈在0至無限大完整的價格域上」所帶來的不足之處日漸顯露,Curve V1 的推出更是直接精準地切走了穩定幣交易對這重要的市場。
在設計V3 時,Uniswap 團隊首先想建構出只在有限連續價格區間內提供流動性的公式,他們建構的起點仍是xy=k 。
想像一下,如果想實現一個效果,在 [Pa, Pb] 價格區間內(例如 [0.99, 1.01] 或是 [1500, 1700]),這個公式對交易的支持就和Uni V1/V2 的xy = k 一模一樣,但當價格超出 [Pa, Pb],就不再提供流動性了。
這種效果對應的公式如下:
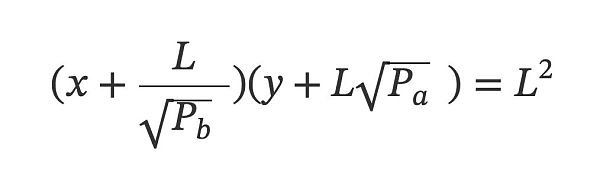
若用圖來呈現,會十分清晰,就是把xy=k 向左下方平移了一些位置。具體要移多少,由Pa、Pb決定。
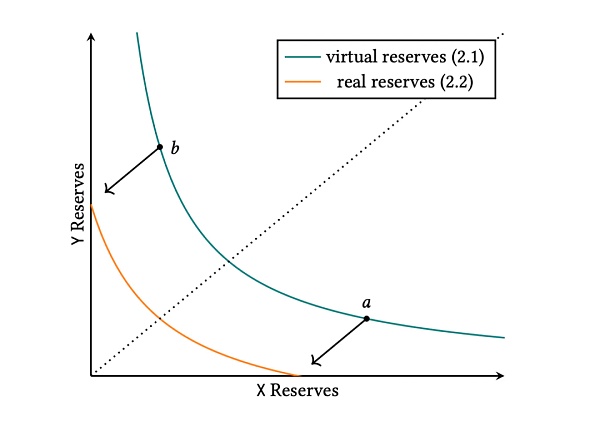
這個公式實現的效果是,所有流動性都集中在 [Pa, Pb] 內,LP 存入一定數量的X_token 和Y_token,在 [Pa, Pb] 價格區間內提供了一些流動性。單就這個局部的流動性效果,若要讓Uni V2 的LP 來達成,則需要LP 去存入更多的X_token 和Y_token;多的程度取決於Pa、Pb,可能需要多很多。
這個平移公式是Uni V3 進一步建構的基礎公式,Uni V3 暫講到這。
3. 奇妙的擦肩而過- 兩種思維路徑的交點
將第1節中Curve V1 的揉合公式做一些變換:
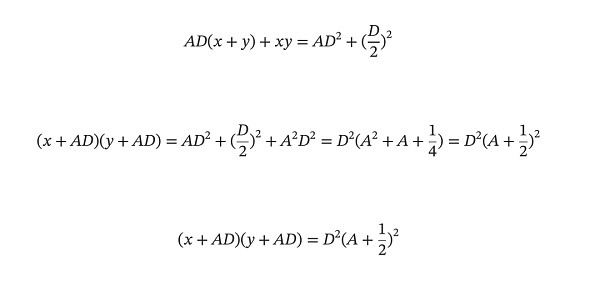
再和第2節中Uni V3 的平移公式放在一起觀察,會發現兩者很像:
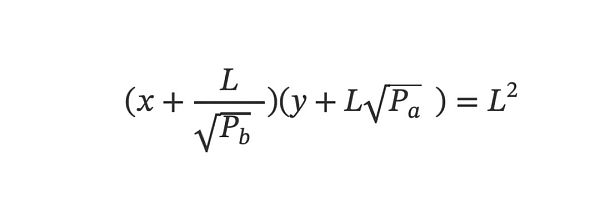
若再對Uni V3 平移公式內的Pa 和Pb 做一些限定,令Pb=1/Pa,也就是限定價格區間為類似 [0.5, 2] 或 [0.01, 100] 這樣的區間,滿足在1:1 價格點兩側倍數意義上的對稱。
做了這個限定之後,可以說兩個公式就是完全一樣了:
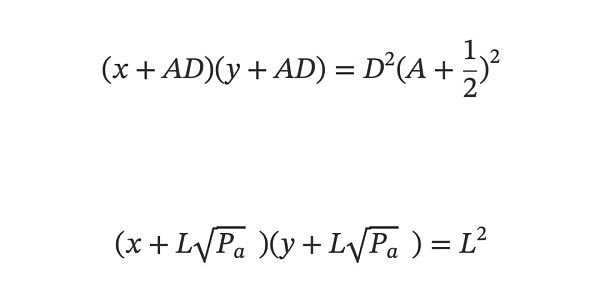
兩個公式裡有著不同的參數表達,可以很輕鬆地推導出兩組參數的關係。我們不妨以Curve V1 揉合公式的參數A 和D 為基礎,計算出L 和Pa,如下:

這些參數的意義和兩個協議各自建構的思考路徑有關,我們結合兩組參數的關係,再簡單回顧一下兩個建構過程。
簡化起見,假設一個穩定幣交易對的池子,初始價格是1:1。 Curve V1 揉合公式中的D 代表了初始LP 投入了兩種穩定幣各D/2 的數量。 A 則代表了這個揉合公式趨近x+y=D 的程度。
來到Uni 這一側,我們再虛擬出一個Uni V2 的穩定幣交易對池子,滿足以下公式:
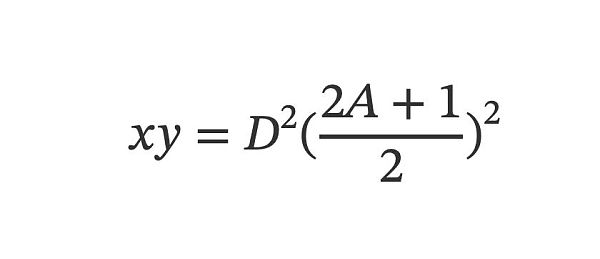
也就是初始價1:1 的話,初始LP 需投入兩種穩定幣各D(2A+1)/2 這麼多的數量。
這時有一個Uni V3 池子,希望實現的效果是,只在以下價格區間提供流動性:
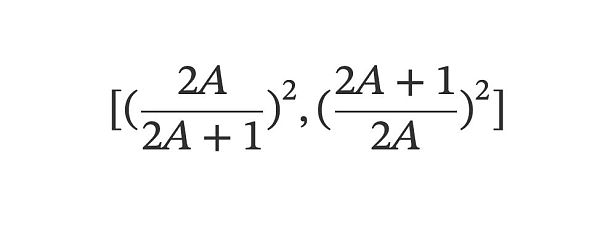
且在這個區間內的流動性效果就如同剛剛虛擬出的Uni V2 池子那般。滿足這個效果的Uni V3 池子所對應的公式恰恰就和前述的Curve V1 揉合公式一模一樣了。
簡單概括的話,Curve V1 透過揉合所實現的效果,恰恰就相當於先虛擬出一個代幣儲備量大很多(多了2A 倍)的Uni V2 池子,然後在 [(2A/(2A+1))², ((2A+1)/2A)²] 價格區間實現了和這個Uni V2 池子完全相同的流動性效果。
4.分道揚鑣- 兩種思考路徑的不同終點
Curve V1 揉合公式就是Uni V3 平移公式的特殊型態。事實上,若在Curve V1 揉合公式內再引入一個參數,x+y 的部分調整為x+py,兩者就完全等價了,這裡不多展開。
Curve V1 在揉合公式的基礎上,Uni V3 在平移公式的基礎上,順著各自原本的思維路徑,繼續前行,分道揚鑣。
4.1 Curve V1:進一步的動態漸層揉合
Curve V1 揉合公式有一個缺陷,只在有限價格區間內提供流動性,Michael 需要的是一個全價格區間都有流動性的公式。 (至於為什麼有這個需求?或許全價格區間都有流動性是很自然的、更加完整健全的狀態,例如在對外提供Oracle 的意義上。)
我們可以這麼來理解他進一步構造的思路:讓這個揉合的程度動態化。之前的揉合公式裡的A 是常數,代表了統一的揉合程度。現在進一步地,當x 偏離D/2 越多(即x 越小或越大時),或者說價格偏離1:1 越多,讓揉合的程度更偏向xy = (D/2)²,x或當價格偏離到極限狀態時,就變成了單純的xy=(D/2)²,這樣就實現了全價區間都有流動性。
Michael 把A 變成了Axy/(D/2)²

這就可以實現上面所講的動態漸變效果。構造方式當然不只限於這一種,我有種感覺Michael 在這一步構造過程裡,並沒有對不同的動態漸變實現方式的差異做很深入的對比研究,或許只要能方便地實現全價格流動性就點到為止了。
終於,我們得到了Curve V1 的最終型態公式如下:
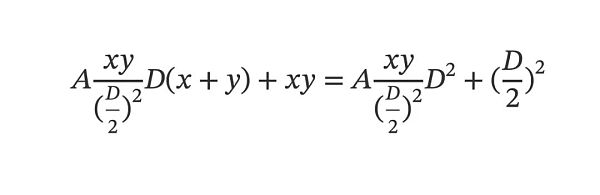
4.2 Uni V3:放棄大一統單一公式,自由組合分段函數
Uni V3 平移公式最核心的內涵在於 [Pa, Pb] 這個價格區間。以這個平移公式作為基礎,很自然地,Uni V3 走向了一個方向;不同價格區間的流動性可以不同(如果不同價格區間的流動性相同,那就又回到Uni V2 了)。
在這個大方向上,仍然有不同的設計分叉。一條分岔路,可以由協議定死一個不同價格區間的流動性分配規則,LP 們仍然是同質的,其實Curve V1 可以看作是這一種類型(價格區間極限小)。
另一條分岔路,所有的決定權全部讓渡給LP 們,LP 們各自獨立的決策共同決定了最終流動性在不同價格區間的分配方式。
Uni V3 選擇了後者,這個選擇極為關鍵,這讓整個市場博弈的元素極大地豐富了起來,價格判斷、波動率判斷、運氣成分等等都捲入了進來,使得流動性市場離充分競爭市場更近了一步。
從數學角度看Uni V3 的進一步構造,乍一看,像是一種非常規的分段函數。不同的價格區間,對應不同的L 值,對應地就是不同的公式,例如以下一個極簡的例子:
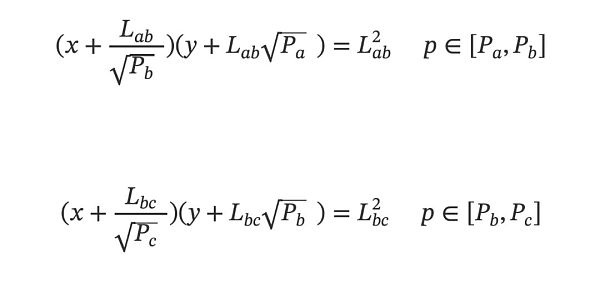
事實上,以上可以轉換為標準的分段函數,即以x 來定義子域,子函數為y 和x 的一個公式,本文不展開。
5. 結語
Curve V1 於2019年底推出,彼時其主要目的就是更能支持穩定幣交易對、填補該市場空缺。或許正是這決定了Michael 的思考路徑,重點是以1:1 價格點對稱的結構,並且流動性相對聚攏在1:1 價格點附近。當Michael 將x+y=D 和xy = (D/2)² 雜交推導出了揉合公式時,在我看來最核心、最具開創性的工作已經完成,因為這個揉合公式已經滿足了上述的對稱、聚攏的特徵。而將揉合公式進一步改造成支持全價格區間流動性的公式,對Michael 而言,或許只是略施小計,收尾工作而已。
Uni V3 更晚才推出,2021年3月白皮書發布。 Uni 團隊已經看到了Curve V1 的足夠長時間的運作。一群極聰明的人,回擊Curve 的方法自然要升維。 Uni 團隊直接打破了一個大前提,LP 們不再「大鍋飯」,可以不再統一地按照每個池子的單一固定公式去提供流動性。
Uni V3 在Uni V1/V2 xy=k 的基礎上,建構出了一個只在特定價格區間提供流動性的一個基礎公式(即上文所說的平移公式)。 Uni V3 要打破LP「大鍋飯」的大前提,於是賦予了LP 們自由,自由地決定在什麼樣的價格區間(或數個區間)提供流動性。 LP 們每個個體獨立自由地決策,匯總到每個池子層面,也會形成一個公式(分段函數),只是這個公式的形狀是動態變化的,絕非之前的AMM 的那種固定形狀模式(部分AMM 可透過治理調整形狀,如Curve V1 調整A 參數)。
這種設計,不僅解決Uni V2 在穩定幣交易對場景下的資金效率低的問題(回擊Curve V1 ),更是在所有的交易對場景,引入了更加充分的競爭,提升了市場整體的資金效率水平。
從歷史背景、根本出發點的差異梳理了一遍之後,再來看我最初所感嘆的Curve V1 揉合公式和Uni V3 平移公式的相似性,又似乎不過是個不值一提的簡單數學巧合罷了。
Reference:
-
https://www.paradigm.xyz/2021/06/uniswap-v3-the-universal-amm
-
https://www.desmos.com/calculator/08gku58vbf?lang=zh-CN

