在”玩賺錢”的理念下，玩家希望在享受遊戲的同時獲得收益。但GameFi受限於較高的GAS成本和不完善的區塊鏈遊戲開發生態，其安全性和透明度都難以獲得玩家認可。這使GameFi走向另一個極端——不斷優化經濟模型和收益，收益週期不斷縮短，最終造成踩踏。在新的週期，L2、全鏈遊戲引擎和ZK技術的普及將為用戶帶來鏈上隱私和更複雜的鏈上遊戲機制。這同時解決了效能、隱私和可信的問題，將焦點從龐氏遊戲轉移到更可信和複雜的鏈上游戲。利用應用層ZK技術遊戲開發者可以輕易建立對互動式隱私場景有明確需求的鏈上戰略遊戲，也為更複雜的可信（鏈上）遊戲場景帶來新的希望。 Salus將透過本文探討新的應用層ZK技術如何幫助遊戲完成場景創新。
技術背景：遞迴zkSNARK的出現
zk-SNARK是一種加密證明系統，在這種結構中，證明者可以證明擁有某些信息，而不洩露該信息，並且證明者和驗證者之間沒有任何交互。
遞歸zkSNARK意味著開發者可以在zkSNARK證明內部驗證另一個zkSNARK 證明，並產生zkSNARK 證明的陳述。遞歸允許zkSNARK 證明者將更多知識壓縮到他們的證明中的同時保持簡潔，且遞歸驗證過程不會明顯減慢。
與一般zkSNARK 相比，遞歸zkSNARK 透過允許將多個證明壓縮為單一證明來提供增強的可擴展性和效率。這種遞歸組合減少了複雜或多步驟過程的計算負載和證明大小，使它們特別有利於發生大量互動和交易的區塊鏈遊戲等應用程式。這將為用戶和開發人員帶來更高的效能並降低成本。
圖片來源- https://ethresear.ch/t/signature-merging-for-large-scale-consensus/17386 遞歸SNARK 解鎖新應用程式層級屬性
- 壓縮
遞歸zkSNARK 允許證明者將「更多知識」放入證明中，同時確保這些證明仍然可以由驗證者在恆定或多對數時間內進行驗證。使用遞歸zkSNARK 作為資訊的“rollup”，可以獨立地“捲起”比最大的（非遞歸）電路更多的計算。
- 可組合性
使用遞歸zkSNARK，可以建立一個證明鏈，在每一步中，證明都會傳遞給一個新的參與者，每個參與者在其中添加自己的知識聲明，但無需了解鏈中其他部分的詳細資訊。
遞歸SNARK的實現
通常，有兩種方法可以實現完全遞歸zkSNARK：一種方法是使用配對友善橢圓曲線的循環，其中透過找到兩條配對友善的曲線來實現有效的遞歸，使得一條曲線的階數等於另一條曲線的場大小；第二種方法是強行通過，並在證明系統本身中簡單地實現單對友善曲線的橢圓曲線運算。
第一種方法，配對友善橢圓曲線的循環，儘管許多研究者仍在探索，但目前想要實現同時滿足配對友善和循環這兩個特性的曲線還很困難。以下內容定義了什麼是配對友善橢圓曲線循環。
定義1: 橢圓曲線的循環是在有限域上定義的橢圓曲線的列表，其中一條曲線上的點的數目循環地等於下一條曲線的定義域的大小。
橢圓曲線的m-cycle是由m條不同的橢圓曲線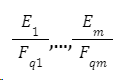
，其中
是質數，使得這些曲線上的點數滿足公式：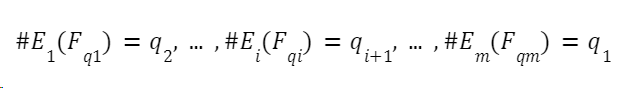
。
高效的zkSNARK方案一般由配對友好型橢圓曲線去構建，而等式中的循環條件使得它們之間可以遞歸組合，並且避免產生在跨不同特徵的有限域時所產生的昂貴的模運算。
定義2: 橢圓曲線的配對友善m-迴圈是一個滿足循環中每條橢圓曲線都是基礎且具有較小嵌入度的m-循環。
第二種方法是強行通過，並在證明系統本身中簡單地實現單對友善曲線的橢圓曲線運算）。你可以將配對電路移植到BN254曲線上，然後在Circom中組裝一個生長驗證器。
以groth16證明系統為例，groth16 有兩個階段的可信設置，第二階段的設置是電路特定的。這意味著，當你在SNARK 內部驗證證明時，它將需要獨立於外層SNARK 的受信任設定。
因此最適合遞歸groth16 SNARK 的是那些遞歸到自身的應用，即在電路中驗證的證明是同一電路本身的證明。這意味著我們只需要一個可信任設定。如圖展示了自遞歸SNARK的思路：
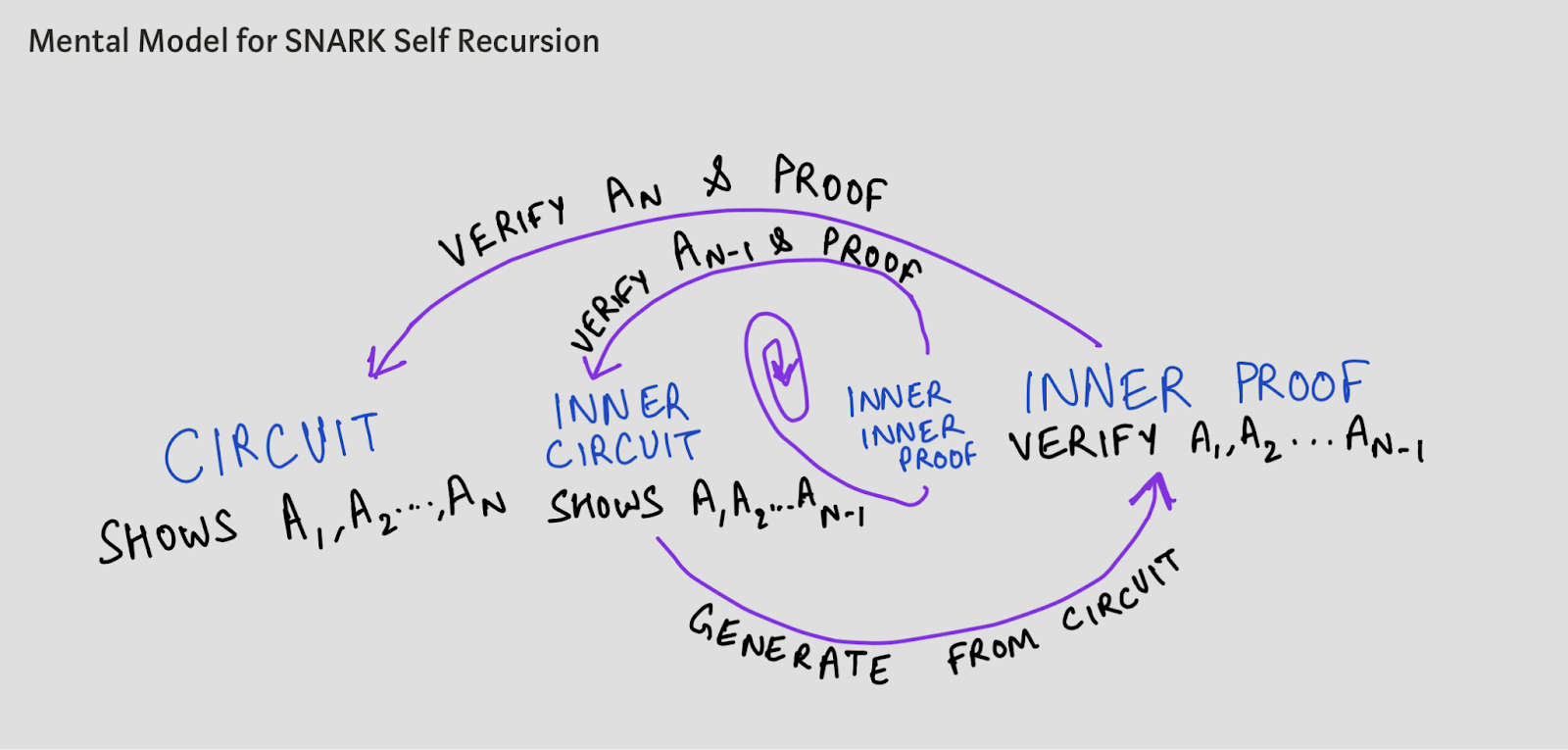
自遞歸SNARK – 圖片來源https://0xparc.org/blog/groth16-recursion
在每一步，你都有一個電路來證明計算
的有效性( 可能i是對SNARK的公開輸入)，並且在第i個這樣的證明中，您驗證另一個計算有效性的證明 
的有效性。還有步驟
的有效性，在每次遞歸時，您的SNARK電路將保持不變。以Isokratia為例，每個
都是ECDSA簽章驗證。
總的來說，遞歸zkSNARK提供了更強的擴展性：減少多步驟遊戲或動作所需的數據和計算，使它們在鏈上更加可行，確保複雜的遊戲邏輯和狀態轉換快速、安全地驗證。
案例研究：ZK-Hunt 及其影響
ZK Hunt 是一款類RTS 的鏈上PvP 遊戲，探索了使用ZK技術實現複雜鏈上游戲機制和資訊不對稱。 ZK Hunt 讓玩家在完全隱私的情況下執行動作，可以在不洩露任何基礎資料的情況下驗證每個動作。
在ZK Hunt平原上的移動是公開的，玩家B 可以看到玩家A 在移動時的位置更新。進入叢林也是公開的，但在叢林中移動是不可見的，因此玩家A 無法確定玩家B 在叢林中的位置，而只能模擬一組不斷增長的潛在位置，這些位置以問號顯示。離開叢林回到平原用戶位置會再次公開，所以這個潛在的位置集合就消失了。
這種資訊隱藏行為是ZK Hunt 的基礎；單位有一個狀態（它們的位置），可以從公共狀態變成私有狀態，然後根據遊戲中的動作再次變回來。這增強了遊戲的策略性。
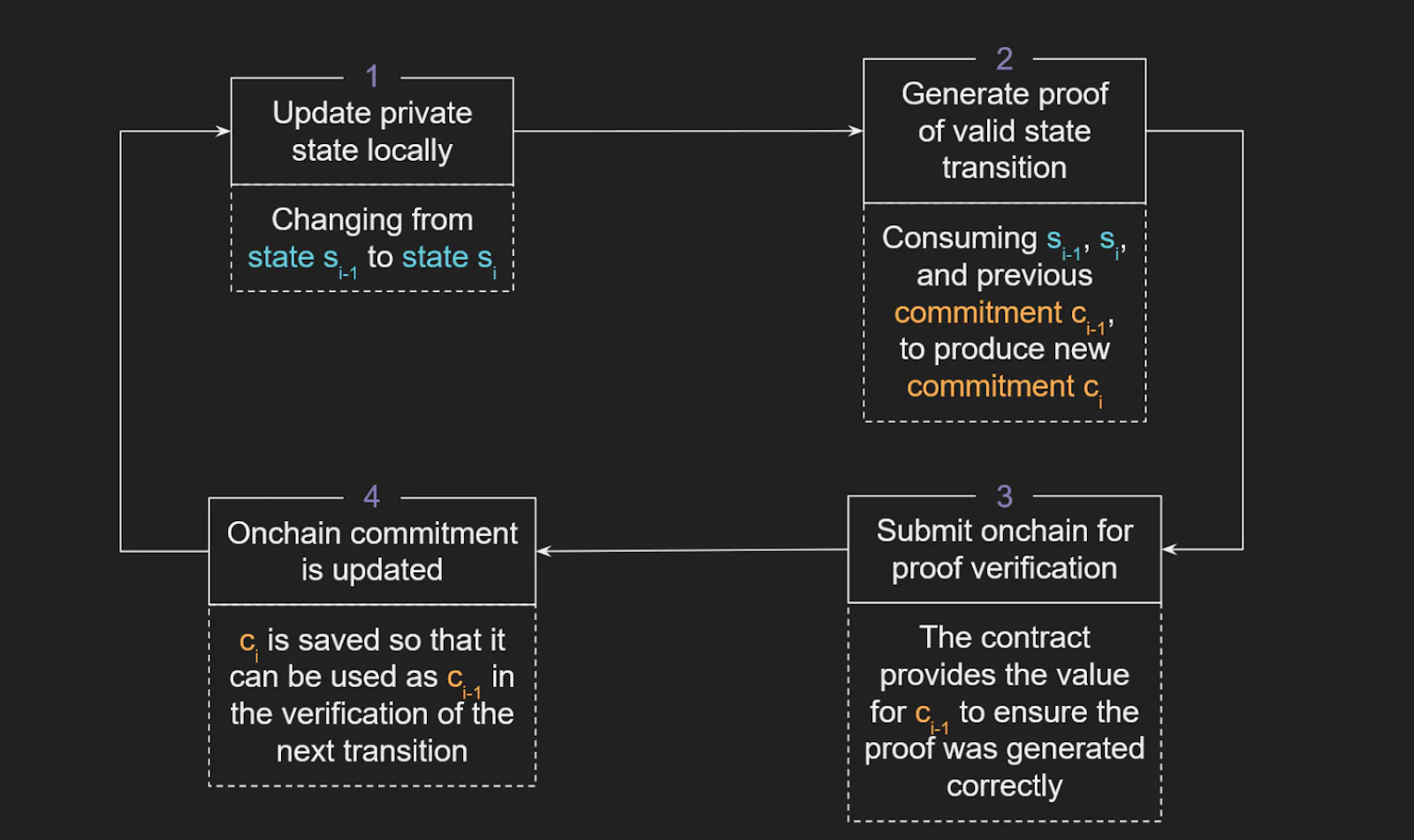
圖片來源：https://gam3s.gg/zk-hunt/
如圖所示：ZK Hunt的狀態驗證流程主要為下列步驟：
- 本地更新私有狀態：從si-1到si（從公開轉為私有或從私有轉為公開）
- 產生有效轉換狀態的證明：消耗si-1 和si（和先前的承諾Ci-1 ,產生新的承諾Ci)
- 提交到鏈上驗證證明（合約為承諾Ci-1 提供了值，以確保正確生成證明）
- 更新鏈上的承諾（保存Ci 以便在下個轉換時可以將其用作Ci-1）
承諾是一種工具，ZK 證明可以使用它來驗證引用用戶先前「承諾」的一些私有狀態，而無需向驗證者透露該狀態。使用者將承諾C 作為公共輸入提供給證明，將私有狀態s 作為私有輸入，證明在內部計算s 將產生的承諾，並檢查它是否與C 匹配：
儘管ZK 證明驗證的成本被認為是恆定的（至少對於某些證明系統，如groth16 等），實際上這個驗證成本會根據公共輸入的數量而增加，這在進行鏈上驗證時可能很重要。同時，ZK Hunt使用了poseidon hash 作為承諾方案，因為它在電路內計算比其他常見雜湊函數效率高得多，每個訊息位元的約束更少。如果私有狀態是從足夠大的範圍（例如私鑰或隨機種子）中隨機選擇的值，那麼只需獲取該值的雜湊值就足以作為承諾。
類似的ZK技術可以實現的遊戲創新場景還有很多，例如資產隱藏、決策隱私和進度保密。
- 資產隱藏：在集換式卡牌遊戲中，玩家可以使用零知識證明隱藏自己的手牌，只在打牌時顯示必要的資訊。
- 決策隱私：在策略遊戲中，玩家可以秘密選擇下一步或分配資源，這些選擇僅在特定點或由遊戲邏輯觸發時才會公開。
- 進度保密：在冒險或角色扮演遊戲中，玩家可能會完成任務或獲得成就，而其他人並不確切知道他們已經完成了哪些任務，從而保持驚喜或競爭保密的元素。
透過採用零知識證明技術，ZK Hunt允許玩家在保持隱私的同時進行遊戲操作。這不僅是技術上的創新，更是鏈上遊戲的規則變革。透過這種方式，遊戲行動在不透露敏感資料的情況下得到驗證，增強了策略的隱蔽性，並豐富了遊戲的策略深度和驚喜元素。