作者：Quantodian 來源：medium 翻譯：善歐巴，金色財經

介紹

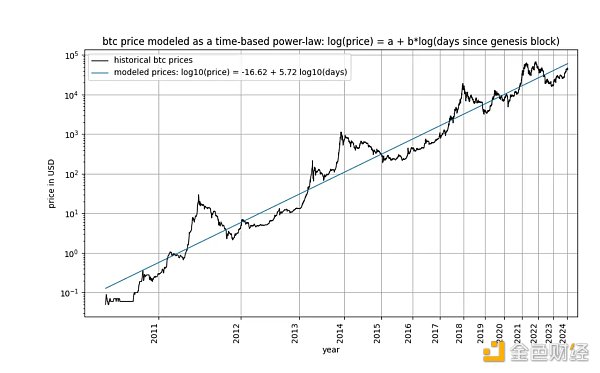
比特幣基於時間的冪律最早由Giovanni Santostasi早在2014 年提出，並在2019 年由我們重新表達（無論是作為走廊還是作為三參數模型），描述了比特幣價格與時間之間的關係。具體來說，該模型描述了自比特幣創世區塊以來的天數對數與比特幣美元價格對數之間的線性關係。

該模型吸引了多位批評者，包括Marcel Burger、Tim Stolte和Nick Emblow，他們各自撰寫了對該模型的「反駁」。在本文中，我們的目的是剖析這三個批評中的一個關鍵論點：所謂的時間和價格之間缺乏協整，將模型視為「無效」並且僅僅表明虛假關係。

真的是這樣嗎？

在這篇文章中，我們將徹底研究這個問題。這使我們得出這樣的結論：嚴格來說，協整不能存在於依賴時間的模型中，包括我們自己的模型。儘管如此，不可否認的是，協整所必需的統計屬性之一存在於基於時間的冪律模型中。因此，我們得出的結論是，基於時間的冪律在鬆散意義上是協整的，我們的批評者是錯誤的，而該模型是完全有效的。我們證明這一結論同樣適用於庫存流量（S2F）模型以及長期股市指數價格中觀察到的指數增長。

概念入門

協整wtf

你已經迷路了嗎？或許「協整」這個詞對你來說比較陌生？別擔心：因果推理和非虛假關係領域的專家、《為什麼之書》的作者Judea Pearl聲稱對這個主題一無所知。我們將努力充分闡明當前問題的相關術語。

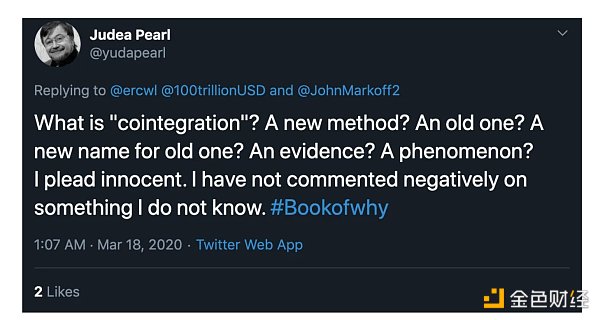
有趣且令人著迷的是#bitcoin 領域內關於X 的激烈的協整爭論，其特點是該主題明顯的膚淺程度。許多存量流量和冪律的追隨者都感到困惑。有興趣的讀者可以透過在X 中輸入搜尋字詞「什麼是協整」來親眼目睹這一點。雖然一些貢獻者似乎隨著時間的推移已經掌握並完善了他們的理解，但其他人仍然感到困惑，轉換陣營或迷失方向。直到現在我們才開始討論這個話題。

首先一些背景

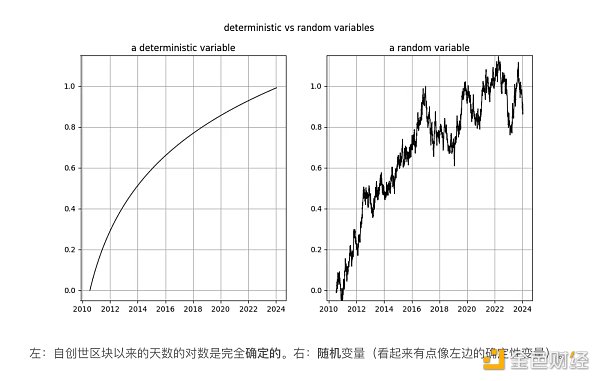
隨機過程涉及隨機變數。隨機變數的值不是預先決定的。相較之下，確定性過程可以提前精確預測——它的每個面向都是事先已知的。像股票市場價格這樣的事情是隨機的，因為我們無法提前預測資產的價格。因此，我們將股票或比特幣價格等時間序列視為隨機變數的觀測值。

相反，時間的流逝遵循確定性模式。每一秒、一秒都過去了——沒有任何不確定性。因此，事件發生後經過的持續時間是一個確定性變數。

一個訊號的平穩性

在研究協整之前，我們先來看看協整的基礎概念：平穩性：

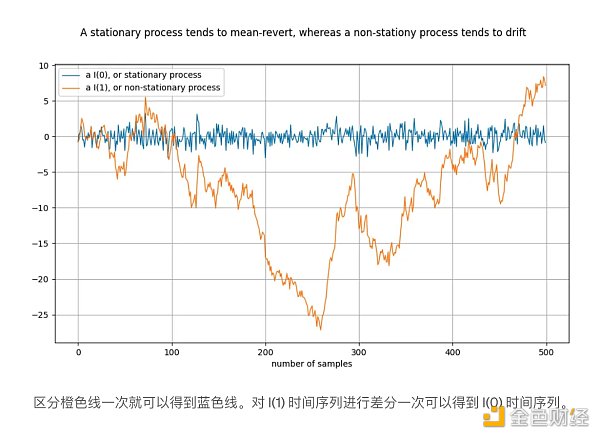
平穩過程是一種隨機過程，廣泛地說，隨著時間的推移，它具有相同的屬性。此類屬性的範例是平均值和方差，對於平穩過程來說，平均值和方差是已定義且穩定的。平穩時間序列的同義詞是I(0)。來自平穩過程的時間序列不應該“漂移”，並且應該傾向於恢復到平均值，通常為零。

非平穩過程的一個例子是隨機遊走，描述了物理學中的布朗運動或粒子擴散：隨機遊走中的每個新值取決於先前的值加上隨機數。非平穩過程的屬性（例如平均值和變異數）隨時間變化，或沒有定義。非平穩過程為I(1) 或更高，但通常為I(1)。源自非平穩過程的時間序列隨時間“漂移”，即傾向於遠離任何固定值。

符號I(1)指的是時間序列在達到平穩之前需要「差分」的頻率。差分是指時間序列中的值與其前一個值之間的差異。這大致相當於求導數。平穩時間序列已經是平穩的－它需要差分0 次才能平穩，因此它是I(0)。 I(1) 時間序列在平穩之前需要進行一次差分。

上圖的建構方式是透過對橘色時間序列進行一次差分來獲得藍色時間序列。等效地，橙色時間序列是透過對藍色時間序列進行積分而得到的。

這裡的單位根過程指的是自迴歸模型（更準確地說是AR(1) 類型），其中rho 參數估計等於1。雖然我們可以互換使用rho 和根，但rho 指的是過程通常是未知的，需要估計。估計結果就是「根」值。

rho 的值表​​示進程記憶其先前值的程度。 u 的值指的是誤差項，假設為白噪音。

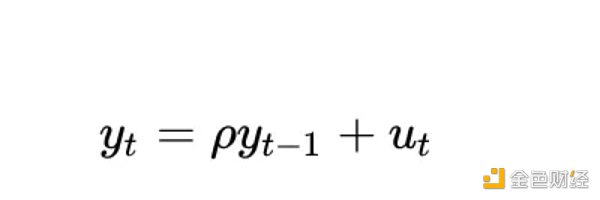
單位根過程是隨機遊走，是非平穩的。 「根」或rho 值低於1 的過程往往不會漂移，因此是靜止的。從長遠來看，即使接近（但低於）1 的值也將傾向於均值回歸（而不是漂移）。因此，單位根過程是特殊的，因為它的行為與根值非常接近1 的過程根本不同。下圖顯示了4 個已知自回歸過程產生的資料的4 個樣本，每個樣本都有不同的rho 值。

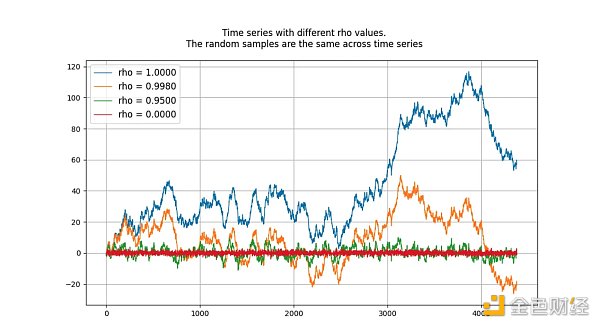
兩個訊號的協整

兩個隨機變數（在我們的例子中為時間序列）之間存在或不存在協整。為了使該對進行協整，兩者必須以相同的階數進行積分並且是非平穩的。此外（這是關鍵部分），兩個時間序列必須存在平穩的線性組合。

無協整訊號的範例

如果兩個時間序列是非平穩的，則線性組合（在這種情況下我們簡單地選擇兩個時間序列之間的差值）通常也是非平穩的：

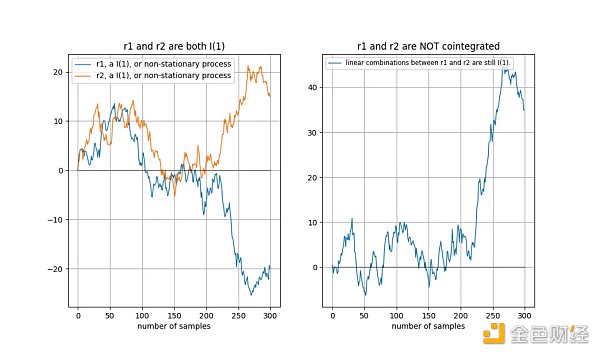
協整訊號的範例

如果兩個非平穩時間序列長期「以相同的方式」漂移，那麼線性組合（這裡我們選擇r2–0.5*r1）可以是平穩的：

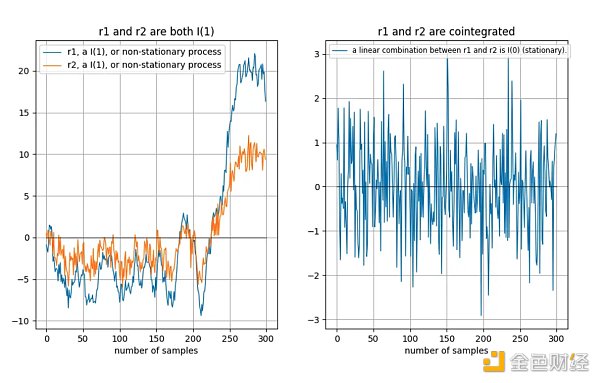
Tu 等人 [1] 很好地直觀地描述了協整：

“時間序列之間存在協整關係意味著它們在長期內具有共同的隨機漂移。”

如果兩個非平穩時間序列具有平穩的線性組合，為什麼有用？假設我們有兩個時間序列x 和y，並且我們嘗試基於x 對y 進行建模：y = a + b*x。我們的模型誤差由x 和y 的線性組合給出：模型誤差= y — a — b*x 。我們希望這個模型誤差是穩定的，即長遠來看不會漂移。如果模型誤差從長遠來看逐漸消失，那就意味著我們的模型很糟糕——無法做出準確的預測。

細節決定成敗

更正式的定義可以在Engle 和Granger 的《協整和誤差修正：表示、估計和檢定》中找到[2]（格蘭傑是協整概念的發明者，並獲得了2003 年諾貝爾經濟學獎），它定義了關鍵概念以及協整檢測的檢驗。論文的關鍵是假設時間序列是隨機的，沒有確定性成分（我們稍後會討論這一點）。

應用於時間和比特幣價格

在基於時間的冪律的情況下，我們有兩個變數：

1. log_time：自創世區塊以來的天數的對數

2. log_price : 價格的對數

根據Engle和Granger的定義，兩個變數都需要是隨機變量，沒有確定性成分，並且需要是非平穩的。此外，我們必須能夠找到兩個變數的平穩線性組合。否則，兩個變數之間不存在協整。

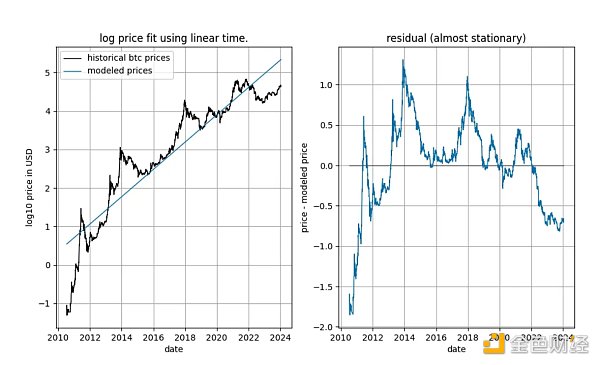
在深入討論細節之前，讓我們先展示一些關於模型資料本身的圖表，沒有任何平穩性或協整概念的概念。請注意，基於時間的冪律產生的擬合在視覺上看起來相當不錯。殘差向量並不立即表明漂移。

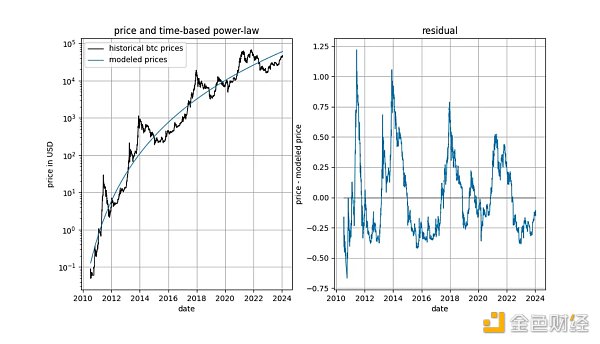
此外，該模型顯示出出色的樣本外性能（見下文）。出色的樣本外表現並不符合模型是虛假的這一說法——基於虛假相關性的模型應該是：虛假的，這意味著它無法準確預測。可以透過將模型擬合到有限數量的資料（直到某個日期）並預測模型不擬合的時間段（類似於交叉驗證）來測試樣本外性能。在樣本外期間，觀察到的價格不斷頻繁地穿越建模價格，觀察到的價格的最大偏移也沒有系統性地遠離建模價格。

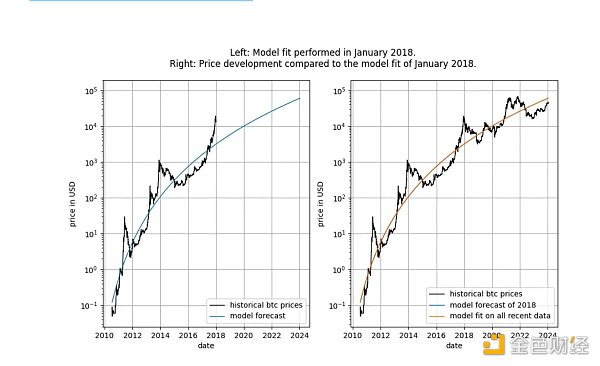
我們可以更嚴格地查看模型發布後（2019 年9 月）的表現，因為模型發布後我們不可能以任何方式作弊——我們無法事後更改模型。

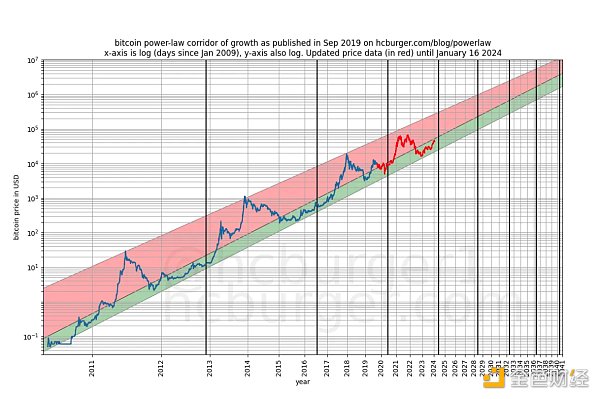
對於任何關於該模型僅是基於虛假相關性的指控，該模型的預測能力都應該持保留態度。

協整逐步

為了使log_time 和log_price 之間可能存在協整，兩個變數都必須是相同階次的隨機變數積分，並且至少為1 階。

log_price 變數

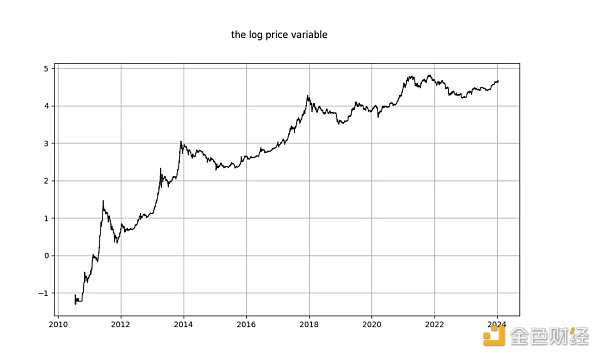
log_price 是平穩時間序列嗎？ Nick得出結論，使用未指定風格的ADF 測試（非平穩性測試）和KPSS 測試（平穩性測試），log（價格）毫無疑問是非平穩的，因此I(1) 或更高。 Marcel Burger以目視檢查得出結論為I(1)。 Tim Stolte做了一個更有趣的觀察：他在不同時間段進行了ADF 測試（未指定風格），並指出情況並不明確：「因此，我們無法堅決拒絕非平穩並得出結論：是對數價格非平穩的跡象。”

讓我們進行自己的分析。與Tim Stolte 類似，我們將在不同的時間窗口應用ADF 測試：始終從第一個可用日期開始，並每天添加一天（我們使用每日數據）。透過這種方式，我們可以看到ADF 測試的結果如何隨時間變化。但與Tim 和Nick 不同的是，我們將指定執行哪個版本的ADF 測試。根據維基百科，DF 和ADF 測試有三種主要風格：

這三個版本之間的差異在於它們能夠適應（消除）不同的趨勢。這與Engle 和Granger 要求刪除任何確定性趨勢有關- 這三個版本能夠刪除三種簡單的確定性趨勢類型。第一個版本嘗試僅使用過去的log_price 資料來描述每日log_price 變化。第二個版本允許使用常數項，其效果是log_price 可以具有線性趨勢（向上或向下）。第三個版本允許二次（拋物線）分量。

我們不知道Tim 和Nick 運行了哪些版本，但我們將運行所有三個版本。

我們在ADF 測試中使用的最大滯後為1，但使用更長的滯後並不會顯著改變我們的結果和結論。我們將使用python 的statsmodels.tsa.stattools.adfuller函數，其中「maxlag」為1，並將使用「n」、「c」和「ct」作為「回歸」參數（相當於上面維基百科描述的三種風格） ）。在下圖中，我們顯示了測試返回的p 值（統計顯著性的度量），其中較低的值意味著較高的平穩性可能性（通常使用0.05 的閾值）。

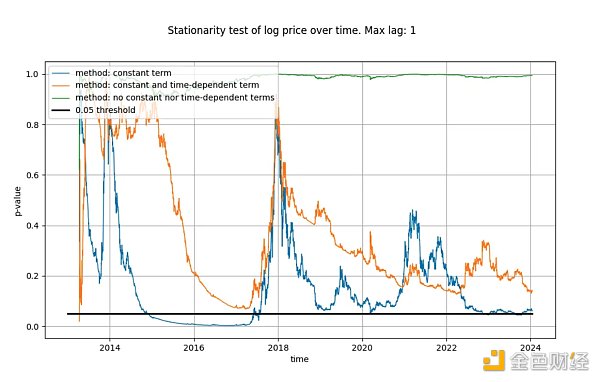
我們觀察到，第一種風格（綠線）明確地得出結論：log_price 時間序列是非平穩的。測試的第三個版本（橙色線）得出相同的結論，但不太果斷。有趣的是，考慮常數項（藍線）的檢定無法確定時間序列是否平穩（Tim很可能也使用了具有常數項的ADF 檢定）。為什麼這三個版本如此不同，特別是為什麼帶有常數項的版本不排除log_price 是平穩的？

只能有一種解釋：在log_price 差異中僅使用常數項（導致log_price 中存在線性項）可以「很好地」擬合時間序列，從而產生看起來幾乎靜止的殘差訊號（儘管具有相當大的開始和結束偏差）。到目前為止，在log_price 中根本不使用確定性趨勢，或使用二次項確定性效應都效果不佳。

這已經給了我們一個強烈的暗示，時間和log_price 之間存在著關係。事實上，如果使用常數項的ADF 測試得出訊號是平穩的結論，這將意味著線性時間項能夠足夠好地逼近log_price 以獲得平穩殘差。獲得平穩殘差是可取的，因為它是非虛假關係的標誌（即我們已經找到了正確的解釋變數）。線性時間趨勢並不完全是我們所需要的，但看起來我們已經很接近了。

我們的結論與馬塞爾·伯格的結論明顯不同，他（在另一篇文章中）指出：

“在之前的分析中，我表明比特幣的價格是一階積分的，而且現在仍然如此。比特幣在價格隨時間的演變中沒有表現出任何確定性因素。”

我們的結論是，線性時間並不能完全解釋比特幣隨時間的價格行為，但絕對清楚log_price 具有確定性的時間元素。此外，在刪除適當的確定性組件（根據恩格爾和格蘭傑的要求）後，log_price 是否為I(1) 尚不清楚。相反，它看起來是趨勢平穩的，但仍然需要找到適當的確定性成分。

如果我們正在尋找協整，那麼log_price 不是I(1) 的事實已經是一個問題，因為對於要協整的兩個變量，它們必須都是I(1) 或更高。

log_time 變數

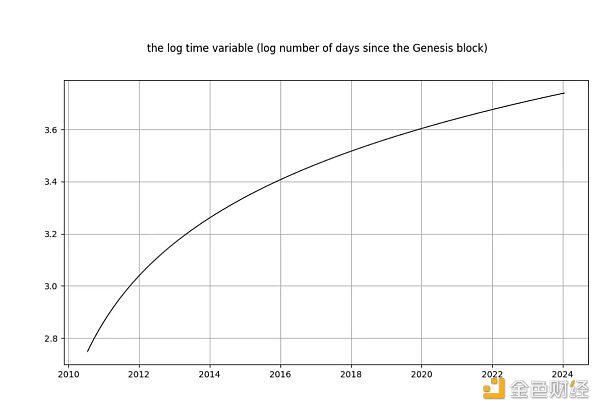
現在讓我們來看看log_time 變數。 Marcel Burger 得出結論，log_time 似乎是六階積分（他一直保持差分直到遇到數值問題）。他期望像對數這樣的數學函數從完全確定性變數轉換為隨機變數的方法是荒謬的。

Nick對於log_time 和log_price 變數得出相同的結論：毫無疑問，它是非平穩的，因此I(1) 或更高。 Tim Stolte 聲稱log_time 在構造上是非平穩的。這些都是令人驚訝的聲明！積分階和協整是指隨機變數的概念，並且從中刪除了任何確定性趨勢（請參閱上面的Engle 和Granger [2]）。提醒一下：確定性變數的值是事先已知的，而隨機變數的值則不然。時間（顯然）是完全確定性的，對數函數也是完全確定性的，因此log_time 也是完全確定性的。

如果我們遵循Engle 和Granger 並從log_time 中刪除確定性趨勢，我們剩下的是一個由零組成的向量，因為log(x) — log(x) = 0，即我們仍然有一個完全確定性的訊號。這意味著我們陷入了困境——我們無法將完全確定性的變數log_time 轉換為隨機變量，因此我們無法使用Engle 和Granger 的框架。

了解協整分析中完全確定性變數的問題有多大的另一種方法是考慮平穩性檢定（例如迪基-富勒檢定）如何處理它。讓我們考慮最簡單的情況（其中y 是感興趣的變量，rho 是要估計的係數，u 是假設為白噪聲的誤差項）：

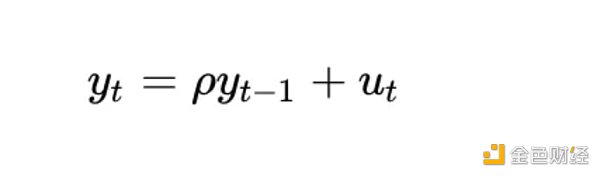
應該發生什麼事？對於t 的所有值，誤差項u_{t} 均為0，因為我們沒有隨機分量— 不需要誤差。但由於log_time 是時間的非線性函數，因此rho 的值也必須取決於時間。

對於隨機變量，該模型更有用，因為變量rho 捕獲了先前隨機值的記憶程度。但如果沒有隨機值，這個模型就沒有意義。

其他類型的測試也存在與確定性變數相同的問題。

因此，完全確定性變數不屬於協整分析。或者換句話說：協整分析不適用於確定性訊號，如果其中一個訊號是確定性的，則協整分析是一種聲稱虛假關係的不合時宜的工具。

怎麼辦？

協整僅在兩個均為I(d) 的變數之間定義，其中d 至少等於1。我們已經證明log_time 是一個完全確定性變量，不能在平穩性檢定中使用。我們不能說log_time 是I(0)、I(1) 還是I(6)。此外，log_price 也不是I(1)，而是趨勢平穩的。

log_time 和log_price 之間未定義協整這一事實是否意味著基於時間的冪律在統計上無效或虛假？

在任何適當的統計分析中使用混合確定性變數和趨勢平穩變數都是完全有效的。正如我們的批評者試圖相信的那樣，協整並不是統計關係分析的中心點。

所以協整是不可能的。但平穩性分析可能仍有一席之地應用於冪律模型。讓我們進一步探討一下。

我們之所以先對輸入變數之間進行協整分析，是因為我們希望找到兩者的平穩線性組合。沒有根本原因說明為什麼不可能將確定性變數(log_time) 和趨勢平穩變數(log_price) 組合起來以獲得平穩變數。因此，我們可以簡單地對殘差進行平穩性測試，而不是尋找嚴格意義上的協整（因為殘差只是兩個輸入訊號的線性組合）。如果殘差是平穩的，即使我們沒有嚴格遵循恩格爾-格蘭傑協整檢驗，我們也會找到平穩的線性組合（這是協整的目標）。

更深入的研究

James G. MacKinnon在他的論文“協整檢定的臨界值”[3] 中準確地解釋了這一點：協整檢定（Engle Granger 檢定）與殘差的平穩性檢定（DF 或ADF 檢定）是一樣的，如果「協整」迴歸」（將log_time 連結到log_price 的迴歸）已經執行：

MacKinnon 重複了這一說法：如果連接log_time 和log_price 的參數是先驗已知的，則可以跳過Engle Granger 協整檢驗，而是可以對殘差執行三種常見風格之一的平穩性檢定（DF或ADF 檢定） ：

因此，我們可以使用兩種方法中的任何一種，除了產生的檢定統計量之外，它們是相同的：

1. 將log_time 擬合到log_price 並計算殘差（誤差）。根據該殘差，計算DF 或更好的ADF 檢定。由此產生的統計數據告訴我們殘差是否平穩。

2. 假設log_time 和log_price 為I(1)，並執行Engle-Granger 協整檢定。得到的統計數據也告訴我們殘差是否平穩。

對於ADF 測試，使用python 的statsmodels.tsa.stattools.adfuller函數；對於Engle-Granger 測試，我們使用statsmodels.tsa.stattools.coint。對於這兩個函數，我們使用不使用常數的風味（隨著時間的推移沒有恆定的漂移），因為我們的殘差不應該包含隨著時間的推移恆定的漂移（因為這意味著隨著時間的推移，模型開始過度或低估價格）。

我們寫道，ADF 和Engle-Granger 檢定是等效的，但這並不完全正確：它們不會產生相同的檢定統計量。 Engle-Granger 協整檢定假設N=2 個隨機變量，而ADF 檢定假設N=1 個隨機變數（N 是自由度的測量）。一個隨機變數可以受到另一個隨機變數或確定性變數的影響，但確定性變數不能受到隨機變數的影響。因此，在我們的例子中（只有一個確定性變數log_time），ADF 測試傳回的統計資料（假設N=1 隨機變數）是首選。原則上，Engle-Granger 和ADF 檢定可能不一致，但實際上，基於時間的模型並非如此。如下圖所示，結論是一樣的：我們得到了一個平穩殘差向量。

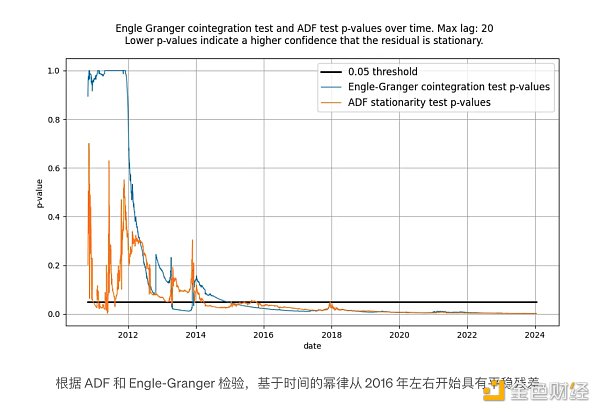
兩項測試最初均未指示平穩殘差，這是正常的。這是因為殘餘訊號中存在低頻分量，可能會被誤認為是非平穩訊號。只有隨著時間的推移，殘差平均值才會明顯恢復並且實際上是靜止的。

S2F 和長期股指價格

S2F 模型似乎已被普遍忽視，因為嚴格意義上的協整被證明是不可能的，其原因與基於時間的冪律相似：（部分）確定性輸入變數。然而，模型產生的殘差看起來非常穩定。

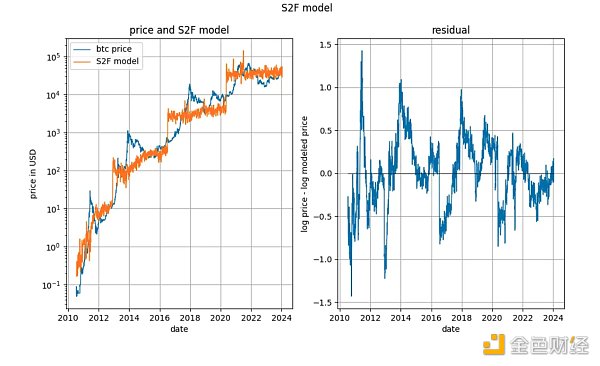
事實上，Engle-Granger 協整檢定和ADF 平穩性檢定（首選，因為有一個確定性變數和一個隨機變數）都產生非常接近0 的p 值。因此，不應排除S2F 模型「缺乏協整」的基礎（實際上意味著「缺乏平穩性」）。

然而，我們在2020 年初指出，還有其他跡象顯示S2F 模式不應該成立。我們預測BTCUSD 價格將低於S2F 模型的預測，事實證明這項預測是有先見之明的。

查看長期股價指數與時間的關係也很有趣（這裡是沒有再投資股息的標準普爾500 指數）。眾所周知，主要股票市場指數平均以7%左右的指數速度成長。事實上，我們透過指數迴歸證實了這一點。

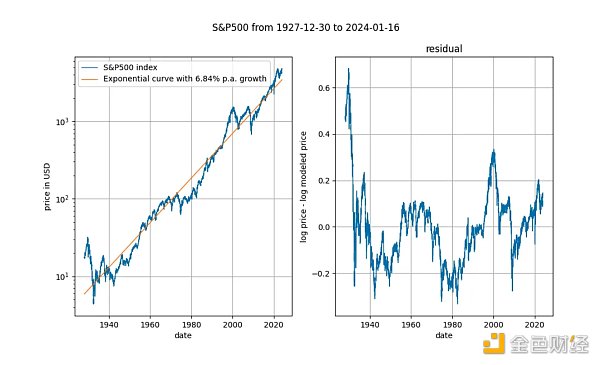
這裡我們再次有一個確定性變數（時間）。 Engle Granger 協整檢定產生約0.025 的p 值，ADF 檢定（首選）產生約0.0075 的p 值（但這些值高度依賴選擇的確切時間段）。再次是平穩殘差。股票價格的指數時間趨勢是有效的。

影響

S2F 模型最初因其良好的計量經濟學基礎（特別是協整的存在）而受到高度讚揚（尤其是Marcel Burger 和Nick Emblow）。隨著潮流的轉變，人們發現S2F 模型無法存在協整（嚴格意義上的），Marcel 和Nick 都跳槽並宣布S2F 模型無效。看來，這次事件之後，人們對S2F模型的看法也改變了。埃里克·沃爾（Eric Wall）對事件的轉變做了精彩的簡短總結。

我們已經解釋過，並且計量經濟學文獻（MacKinnon [3]）也同意我們的觀點，即協整性和平穩性幾乎可以互換使用（統計值除外）。利用這項見解，我們發現S2F 模型在協整/平穩性方面沒有任何問題，因此因為假設缺乏協整而改變對S2F 模型的看法是錯誤的。我們同意S2F 模型是錯誤的，但它的錯誤除了缺乏協整之外還有其他原因。

比特幣基於時間的冪律因其缺乏協整性而受到批評，據稱將log_time 和log_price 之間的關係標記為虛假關係。我們已經證明，比特幣基於時間的冪律具有明顯靜止的殘差，因此我們批評者的推理路線是沒有意義的。

比特幣基於時間的冪律模型是有效、穩定且強大的。一如既往。