作者:Maggie@Foresight Ventures
TL;DR:
-
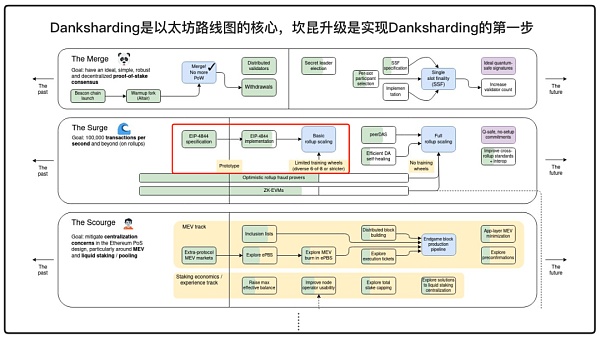
坎昆升級將於2024 年3 月13 日推出,EIP4844即將上線。 Danksharding是以太坊路線圖的核心,這次升級是實現Danksharding的第一步。
-
Ethereum L2適配EIP4844後,交易手續費大幅下降,L2的TPS倍增。用戶會感覺到交易速度更快、成本更低、體驗更流暢、更靈敏。這些L2上會有更複雜更大型的Dapp應用。
-
Optimistic rollups適配EIP4844比較簡單,ZK rollups適合比較複雜。以太坊沒有預先編譯合約支援BLS12-381橢圓曲線,導致部分ZKP驗證難度高,阻礙了ZK rollups適配EIP4844的進度。
-
橢圓曲線的問題可以透過兩種方式解決,1. 等待以太幣對BLS12-381橢圓曲線進行預編譯;2.用另一種證明方式來達到同等目的,使用以太坊預編譯支持的BN254.
-
目前,Arbitrum、Optimistic、Starknet、zkSync、Scroll、Polygon zkEVM以及新L2 Morph都在適合EIP4844。其中,Arbitrum、Optimistic 和Starknet表示坎昆升級後會實施EIP4844的適配。 Morph則率先發布了創新的zkSNARK zkEVM適配方案,這將是第一個適配EIP4844的zkSNARK zkEVM
一、背景
2020 年,以太坊發布的“以Rollup 為中心的以太坊路線圖”,以及第二年Vitalik發表的“Endgame”中描述的以太坊的最終圖景,確定了以太坊的大方向:優化以太坊的基礎層建設,為Rollup服務。
以太坊設計了Danksharding的分片技術以提高以太坊作為資料可用性層的可用性。它將顯著降低L2的交易手續費,提高Rollup的TPS,實現以太坊的大幅擴容
直到今年,以太坊坎昆-德內布(Dencun)升級終於在2024 年3 月13 日推出,EIP4844即將上線,這次硬分叉可以說是以太坊實現Danksharding的第一步,是以太坊路線圖核心中的核心。
關於什麼是DA層,Danksharding的技術原理,EIP4844的內容,請參考去年我寫的一篇技術文章:DA(數據可用性)Summer 將至? https://foresightnews.pro/article/detail/33575
二、坎昆升級如何利好L2?
EIP4844引入了一種新的交易類型,稱為blob-carrying交易。每個blob-carrying交易都可以「攜帶」一個Blob 清單。 Blob 是一個資料包,大約125 KB。 Blob儲存的時間很短,僅4096個epoch,略多於18天。
-
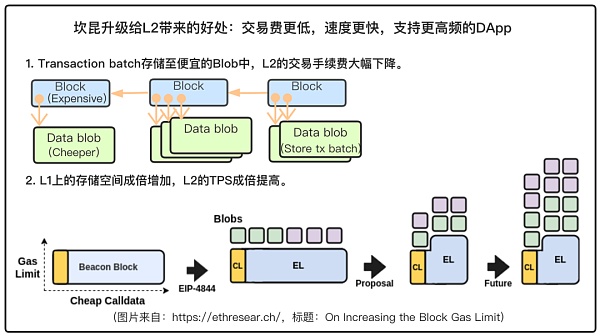
L2交易手續費大幅下降。由於Blob不需要永久存儲,Blob相比於區塊空間更大更便宜。 Blob 可以在相同的gas 消耗下儲存比Calldata 多10 倍的資料。適配了EIP4844的Rollup可以將交易資料儲存在Blob 中,將交易費用降低一個數量級。
-
L2的TPS倍增。目前每個區塊目標是3個Blob,最多允許6 個Blob。區塊只有90KB,而每個Blob大約125KB。引進Blob相當於區塊額外擴展了幾倍的空間可以用來存Rollup的數據,因此Rollup的TPS也能倍增。而Toni和Vitalic寫的「On Increasing the Block Gas Limit」中表示,會透過增加區塊Gas limit和非零Calldata bytes的價格,實現更小、變數更少的區塊大小,從而未來可以增加更多Blob。 Blob更多則儲存空間會更大。
對最終用戶而言,Ethereum L2適配EIP4844後,交易速度更快、成本更低、體驗更流暢、反應更靈敏。這些L2上會有更複雜更大型的Dapp應用。
三、L2如何適配EIP4844?
L2如何適應EIP4844呢?我們需要分Optimistic Rollup和ZK Rollup來分別討論。
Optimistic Rollups適合EIP4844
Optimistic rollup是透過詐欺證明來保證rollup執行的正確性的。即節點首先選擇相信狀態的轉換是正確的,除非有人在規定的時間內發起欺詐證明,證明之前提交的是狀態轉換是不合法的,則該狀態轉換會被撤銷。
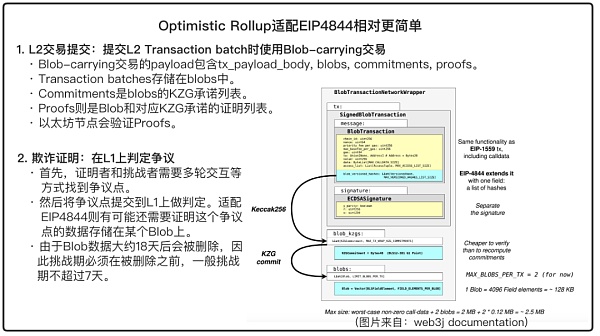
Optimistic Rollup適配EIP4844相對ZK rollup來說比較簡單。把L2的交易都透過Blob-carrying交易提交到L1即可完成適配。此外,就是要調整詐欺證明使之適配EIP4844,這部分就可以慢慢做了。畢竟,許多optimistic rollup至今也沒上線詐欺證明。上線了詐欺證明的,發現兩年多都沒有一個詐欺證明提交。
-
L2交易提交:Rollup提交的時候,使用Blob-carrying交易,將Rollup資料儲存在Blob中。 Blob-carrying交易的payload是rlp([tx_payload_body, blobs, commitments, proofs]) ,其中
-
tx_payload_body – 是標準EIP-2718 blob 交易的TransactionPayloadBody。
-
blobs – Blob 清單。一個交易最多包含兩個blob。
-
commitments – Blob的KZG承諾清單。
-
proofs – Blob和對應KZG承諾的證明清單。這個證明是會被ETH節點所驗證的。
-
調整詐欺證明:
-
首先,證明者和挑戰者需要多輪互動等方式找到爭議點。
-
然後將爭議點提交到L1上做判定。適配EIP4844則有可能還需要證明這個爭議點的資料儲存在某個Blob上。
-
由於Blob資料大約18天後會被刪除,因此挑戰期必須在刪除之前,這一點現在的optimistic rollups都是滿足的。一般挑戰期不超過7天。
ZK Rollups適配EIP4844
ZK rollup是透過ZKP來證明L2狀態轉換是正確的。 ZK rollup適配EIP4844相對optimistic rollup來說更複雜。

1.L2交易提交:這一步Optimistic Rollup是相似的。
2.ZK證明提交:與適配前的ZK Rollup相比,除了做狀態轉換的ZKP證明以外,還需要多證明一個流程。即證明blob commitment和transaction batch是對應的,從而保證狀態轉換證明的輸入是正確的。
打個比方:狀態轉換的ZK電路能產生計算過程a + a = b的證明。當(a=1,b=2)和(a=2,b=4)時產生的ZKP都是合法的。因此我還需要提供一個證明,證明我當時提供的輸入是(a=1,b=2)而不是(a=2,b=4)。
這一點在適配EIP4844之前是不需要做的,因為資料就直接儲存在Calldata中可以直接讀取,確保了輸入不會被調包。用了EIP4844後,Blob資料無法直接讀取,只能透過一個新的電路來證明這一點。
用STARK的ZK rollup(如Starknet)更容易實現這種證明機制。而這對於用SNARK的ZK rollup是存在挑戰的,原因是:EIP4844的blob commitment使用的橢圓曲線是BLS12-381,而ETH的預編譯合約只支持了BN254,由於曲線不同,導致我們難以直接在智能合約中驗證blob commitment完成證明。
-
用SNARK的zkEVM/zkVM需要解決第2點中提到的由於曲線不匹配無法產生ZK證明的問題。
-
等待Ethereum支援BLS12-381的預編譯合約。這會很漫長。
-
採取另一種證明方式來證明。要設計新的電路,必須用預編譯合約支援的BN254橢圓曲線。目前,我們看到Morph採用了這個方法。這也使得Morph成為第一位完成EIP4844適配的zkEVM。
Morph 的EIP-4844 zkEVM 整合解決方案請參閱:https://medium.com/@morphlayer2/morphs-solution-to-eip-4844-zkevm-integration-7f469910478f
四、有哪些L2適配了EIP4844?
Optimistic rollup中,Optimism和Arbitrum已表示致力於採用EIP-4844,並與其社群密切合作來測試和部署必要的更新。 Arbitrum屬於Stage 1的Rollup, 安全性相對較好。涉及到需要將詐欺證明適配EIP4844的問題。 Optimistic rollup屬於是Stage 0的Rollup,目前還沒有詐欺證明,適合起來更容易,但安全性不夠高。
在ZK rollup中,使用STRAK和SNARK的rollup適合度是不同的。用STARK的rollup適配EIP4844比較簡單,Starknet是其中的代表。 Starknet發表了文章表示坎昆升級後會實施對EIP4844的適配(文章連結)。用SNARK的rollup,zkSync也在探索如何利用攜帶blob 的交易來進一步降低成本並提高效能。 Scroll則是在去年發表了一篇文章介紹了適合EIP4844的想法(文章連結)
最令人映像深刻的是Morph, 他是一個Optimistic ZK Rollup,率先發布了zkEVM適配EIP4844的方案,可以說是第一個完成EIP4844的zkEVM Rollup。
Optimistic ZK Rollup結合了兩類Rollup的優點。它樂觀地相信Sequencer提交的執行結果,允許對結果產生懷疑的人發起挑戰。只有在發起挑戰時,證明者才會產生ZKP來證明執行結果的正確性。它擁有Optimistic rollup的效率,又擁有ZK rollup的ZK證明的可靠性。