作者:Jason, ETHconomics Research Space
非常感謝Colin@colinlyguo 參與本文的討論與提供的意見,以及Qi Zhou@qc_qizhou 對本文的回饋。
寫在前面
在EIP-4844 經濟學系列中,我們將分四部分來講述新增的blob-carrying transaction會為網路帶來何種影響。在上一篇文章中,筆者深入Blob 交易的費用機制,包括Blob 交易的費用計算方式,Blob 交易的特質以及Blob Base Fee 的更新演算法等內容。在本篇文章中,筆者基於EIP-4844 Economics and Rollup Strategies的分析框架進一步挖掘EIP-4844 新引入的Blob 市場會如何影響其主要的需求方Rollup 的數據可用策略。
EIP-4844 經濟學系列:
- EIP-4844 經濟學#1: 深入EIP-4844 費用機制
- EIP-4844 經濟學#2: 深入Rollup 資料可用策略(本文)
- EIP-4844 經濟學#3: 深入多維資源定價
- EIP-4844 經濟學#4: 深入Type 3 交易打包策略
Rollup 資料可用策略
EIP-4844 引進了Blob 資料空間作為更佳的資料可用方案。似乎對於Rollup 而言,只需要技術性地升級其密碼學承諾演算法以支援Blob 即可。然而,除了技術底層的升級外,Rollup 更需要研究如何利用Blob 盡可能降低其可用性資料的成本。換而言之,Rollup 需要根據各自的成本曲線以及需求曲線來制定其數據可用的策略。
模型假設分析
建模分析的有效性取決於模型假設。模型假設肯定是無法完全貼近現實,需要做得到抓小放大,關鍵在於假設的合理性以及對分析的影響。因此,在進行模型推導前,我們先來分析本文所依賴的一些關鍵假設。
假設1:引入隱性的延遲成本
在建模過程中,除了資料可用方法消耗的手續費外,本文還引入了隱性的資料延遲成本。資料延遲成本可能對於大部分人而言不太直覺。舉一個極端例子,例如一個rollup 的TPS 是每天1 筆交易,等待這些交易塞滿一個Blob 才提交至L1 似乎不是一個優秀的策略。
資料延遲成本的隱形來自於其主要關聯於使用者體驗,某些去中心化應用的安全模型,以及某些去中心化應用的活性。
- L2 的優勢在於其之上的交易能夠得到L1 的確認。雖然序列器能夠快速返回L2 交易處理結果,但是若L2 交易未得到L1 的確認,中心化的序列器實際上比Polygon 等L1 安全性更差。因此,L2 的目標使用者理應關注L2 交易的可用性資料被提交至L1事件以判斷交易的狀態,並依賴該狀態進行後續操作。因此,資料延遲越大,使用者需要等待時間越長,使用者體驗越差
- 以跨L2 應用為例,此類應用程式最終的安全性都依賴被提交至L1 的L2 可用性資料。因此,此類應用程式的一些關鍵功能需要等待相應的L2 交易的可用性資料上傳後才可以實現。
- 對於zkrollup 而言,L2 交易的可用性資料以及有效性證明被提交至L1時L2 交易立即得到L1 確認。然而,對於optimistic rollup 而言,L2 交易的可用性資料提交至L1後仍需等待一段挑戰期(如7 天)。在該情況下,似乎L2 交易的可用性數據的及時提交沒那麼重要。實際上並不然,因為有些應用(如Maker Bridge)會直接執行驗證提交至L1 的L2 的可用性數據,而無需等待挑戰期。
假設2:資料延遲成本與交易等待時長成正比
本文假設資料延遲成本與交易等待時長成正比(線性函數)。現實中,延遲成本應該更適合用非線形的函數來刻畫。例如,
- 指數函數(延遲成本隨時間指數上升)
- 分段函數(超過某個閾值才引入延遲成本)
相對於上面更精細的刻畫,線形函數具有以下優勢:
- 導數是常數,方便建模推導
- 連續可導,建模過程中的導數運算
同時,線形函數整體上也刻畫了交易等待時長越大,資料延遲成本越高的關鍵特徵,滿足建模的需求。不同的線性比例也能捕捉擬合非線形函數。
假設3:智能合約處理可用性資料的Gas 消耗為常數
本文在Blob 的可用策略和Calldata 和Blob 間的可用策略中假設智能合約處理可用性資料的Gas 消耗為常數,與交易批次中的交易量無關。
在實際場景中,處理可用性資料的Gas 消耗可能是與交易量成線性關係的。例如,交易批次中全是L2 → L1 的操作,那麼智能合約可能需要逐一處理這些操作,因此處理可用性資料的Gas 消耗也會呈現線性關係的。
若對處理可用性資料的Gas 消耗感興趣,可以以Scroll 為例進行洞察:https://github.com/scroll-tech/scroll/pull/659。值得注意的是,EIP-4844 之後,計算交易witness 的keccak256 消耗的gas 可以省去。
根據統計數據可以發現,各個layer 2處理可用性資料的方式其實不太一樣。下面挑選典型例子來說明:
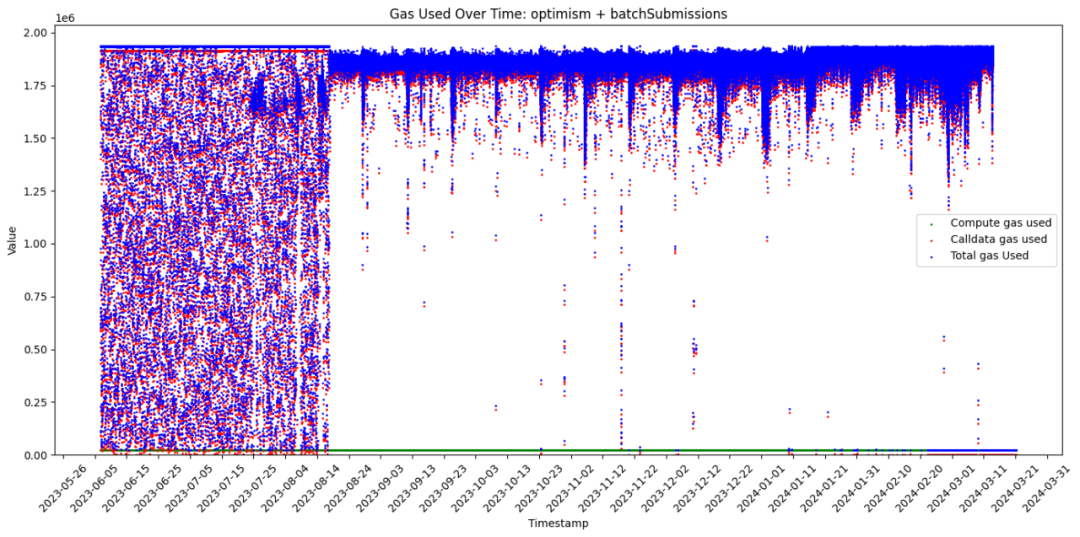
1. Optimism 中處理可用性資料消耗的Gas 基本上與交易批次的大小無關,十分符合本文的假設。
cr:@donnoh_eth
2. Arbitrum 中處理可用性資料消耗的Gas 基本上與交易批次的大小呈正相關,似乎不太符合本文的假設。固定的部分達到175000 Gas,可變部分最大達到90000 Gas,比例約為51.4%。某種程度而言,該假設仍是合理的。
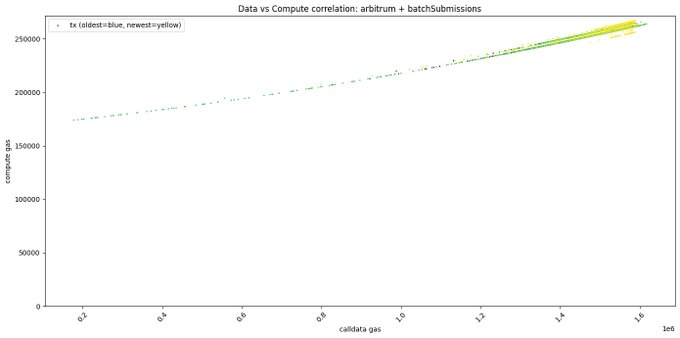
cr:@donnoh_eth 假設4:智能合約處理可用性資料的Gas 可忽略
本文在Blob 均衡價格,Blob 拼單策略以及Blob 成本分攤的推導中假設智能合約處理可用性資料的Gas 消耗可忽略,即遠低於上傳可用性資料的成本。
在EIP-4844 之前,根據統計數據,該假設很明顯是成立的:
 cr:@donnoh_eth
cr:@donnoh_eth
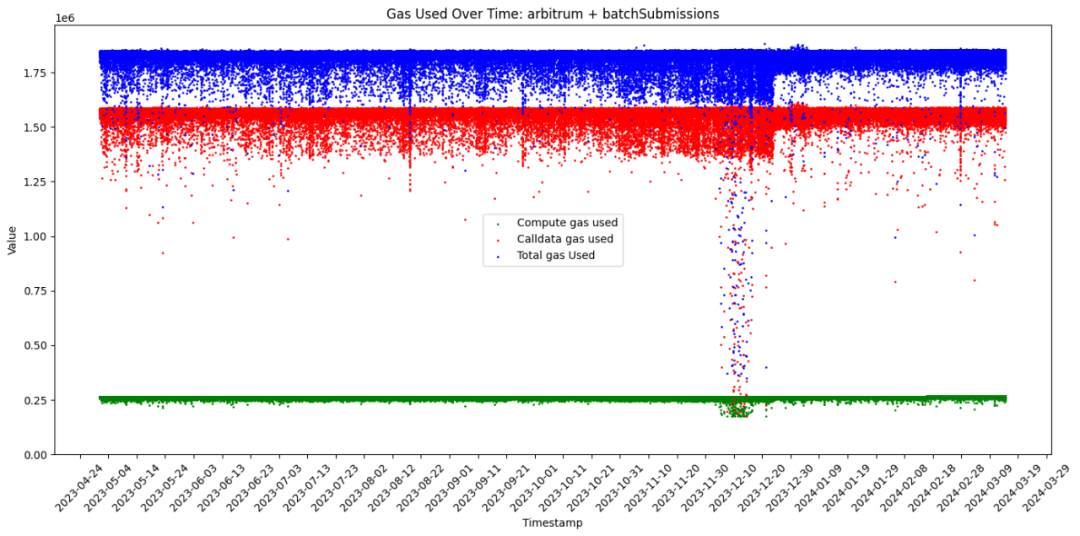 cr:@donnoh_eth
cr:@donnoh_eth
然而,EIP-4844 上線前期,Blob 的費用似乎可以忽略不計,請參閱Optimism 的一個batch 交易。這個時期Blob 的供給遠高於需求,Data Gas Price 為1 wei。
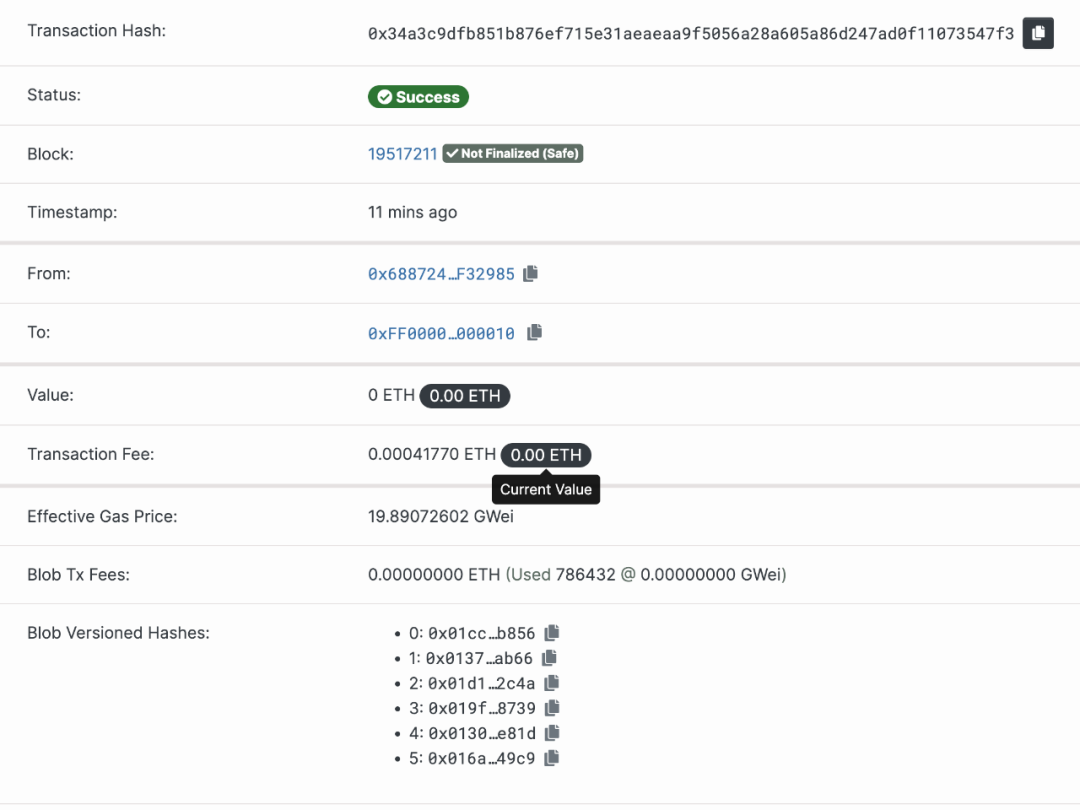 cr:beaconcha.in
cr:beaconcha.in
雖然不符合當前情況,但是該假設在探討上述三個主題還是有意義的
- Blob 均衡價格探討的是Blob 在未來達到供給需求平衡時的場景
- Blob 拼單策略以及Blob 成本分攤探討的是Blob 成本過高而需要拼單的場景
💡 目前(2024.3.31)的Blob 已經錨定了目標,更接近建模假設:
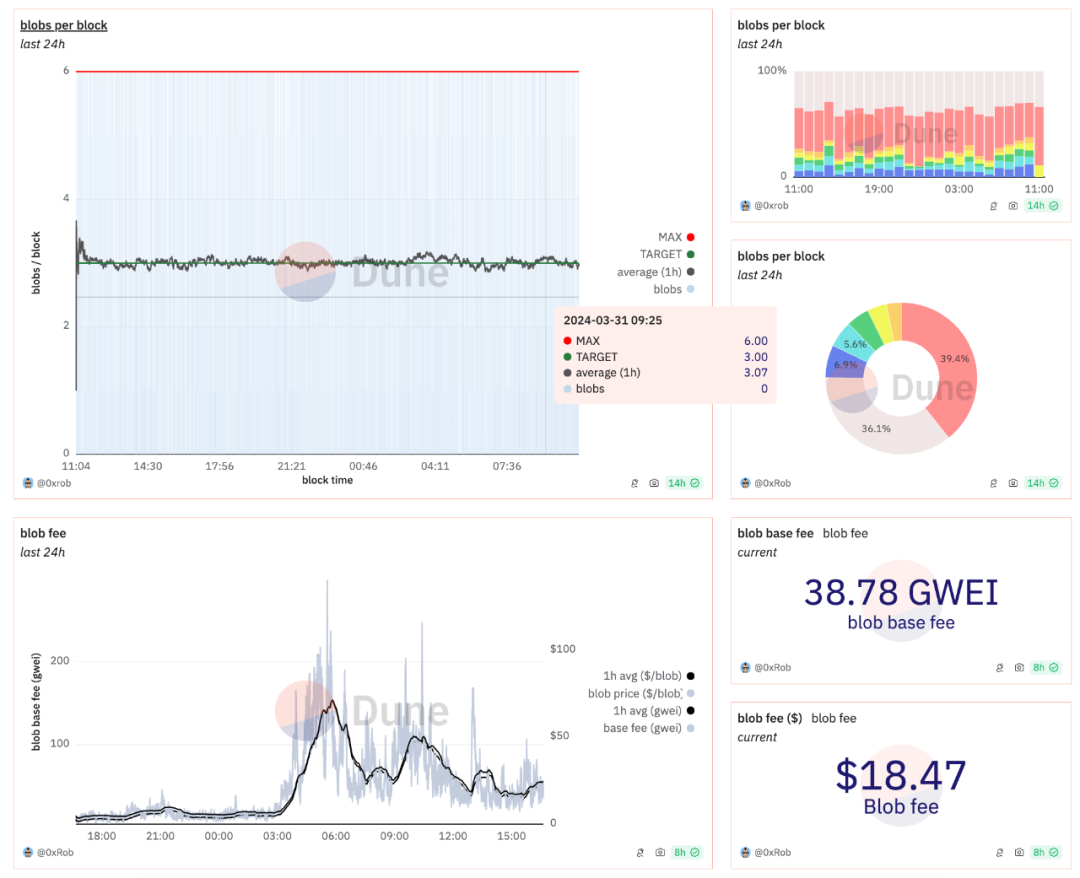
cr: @0xRob 假設5:Gas Price 和Data Gas Price 為靜態均衡值
本文在推導的過程中假設Gas Price 以及Data Gas Price 為靜態均衡值。實際上,均衡值會受供需範式轉移的影響,也是動態的。不過,供需範式轉移(非隨機波動)發生的頻率較低。在這中間,均衡值可以考慮為靜態值,不會影響在這中間實作的策略。不過,供需範式轉移轉移後,要更新新的狀態均衡值即可。
Blob 的可用策略
在EIP-4844 中,Blob 採用的是貨櫃的收費模型。因此,對於Rollup 而言,需要權衡:
當Blob 完全利用時,上傳可用性資料均攤成本是最低的
當Blob 被完全利用時,資料延遲成本是最高的(等待最長時間才能提交至一層網路)
Blob 資料可用方案成本


Calldata 和Blob 間的可用策略
Blob 作為一種資料可用方案,並非完全優於Calldata:
- 利用Calldata 上傳可用性資料的均攤成本是不變的,無需如Blob 般等待資料達到某種量級以降低成本,因此可以做到快速發布,因而有著更低的資料延遲成本。
- 可以預想,有著較少交易量的Rollup 會更傾向於使用Calldata。這些Rollup 需要付出很大的資料延遲成本才能填滿Blob 。
Calldata 資料可用方案成本



然而,Vitalik 基於技術的角度更傾向於限制Calldata 的使用,讓Rollup 都使用Blob:
- 對Rollup 而言,維護兩套機製成本太高。
- Calldata 本身不是為資料可用而設計的。
關於提高Calldata 作為資料可用性方案成本的EIP-7623(Draft)也被提出。基本想法很簡單:
- 若交易Gas 消耗中Calldata 的佔比>~ 76%,Calldata 的成本為68 gas/byte
- 若交易Gas 消耗中Calldata 的佔比< 76%,Calldata 的成本為16 gas/byte
該EIP 隱含一個假設,若Calldata 的佔比>~ 76%,那麼該交易就被認定為資料可用。該值是透過歷史統計權衡出來的:
- 觀察資料可用交易的Calldata 的佔比,盡可能命中
- 觀察非資料可用交易的Calldata 的佔比,盡可能不要誤傷
Blob 均衡價格


Blob 拼單策略
Blob 的聯合發布似乎可以解決Blob 資料延遲成本過高的問題,類比現實世界的貨櫃也不限於只裝一家的貨物。
本章節評估在下列三種場景下,拼單策略導致Blob 均衡價格的變化,並分析拼單策略是否相對單獨發佈為更優策略。
- Rollup i 和Rollup j 都採用Blob 作為資料可用方案
- Rollup i 採用Blob 作為資料可用方案,而Rolup j 則採用Calldata 作為資料可用方案
- Rollup i 和Rollup j 都採用Calldata 作為資料可用方案

場景1:Rollup i 和Rollup j 都採用Blob 作為資料可用方案
場景1 中Blob 的均衡價格會降低,最多降低一半


場景1 中拼單策略相對單獨發佈為更優策略


場景2:Rollup i 採用Blob 作為資料可用方案,而Rolup j 則採用Calldata 作為資料可用方案
場景2 中Blob 的均衡價格會上升,最多為原來的2 倍

場景2 中拼單策略相對單獨發布不一定是更優策略


場景3:Rollup i 和Rollup j 都採用Calldata 作為資料可用方案

場景3 中拼單策略相對單獨發布不一定是更優策略


Blob 成本分攤


性質1:必然存在最佳成本均攤方案

性質2:大型Rollup 需要支付低於其交易比例的Blob 費用

性質3:大型Rollup 需要支付超過一半的Blob 費用

性質4:小型Rollup 單筆交易成本優化效果較佳
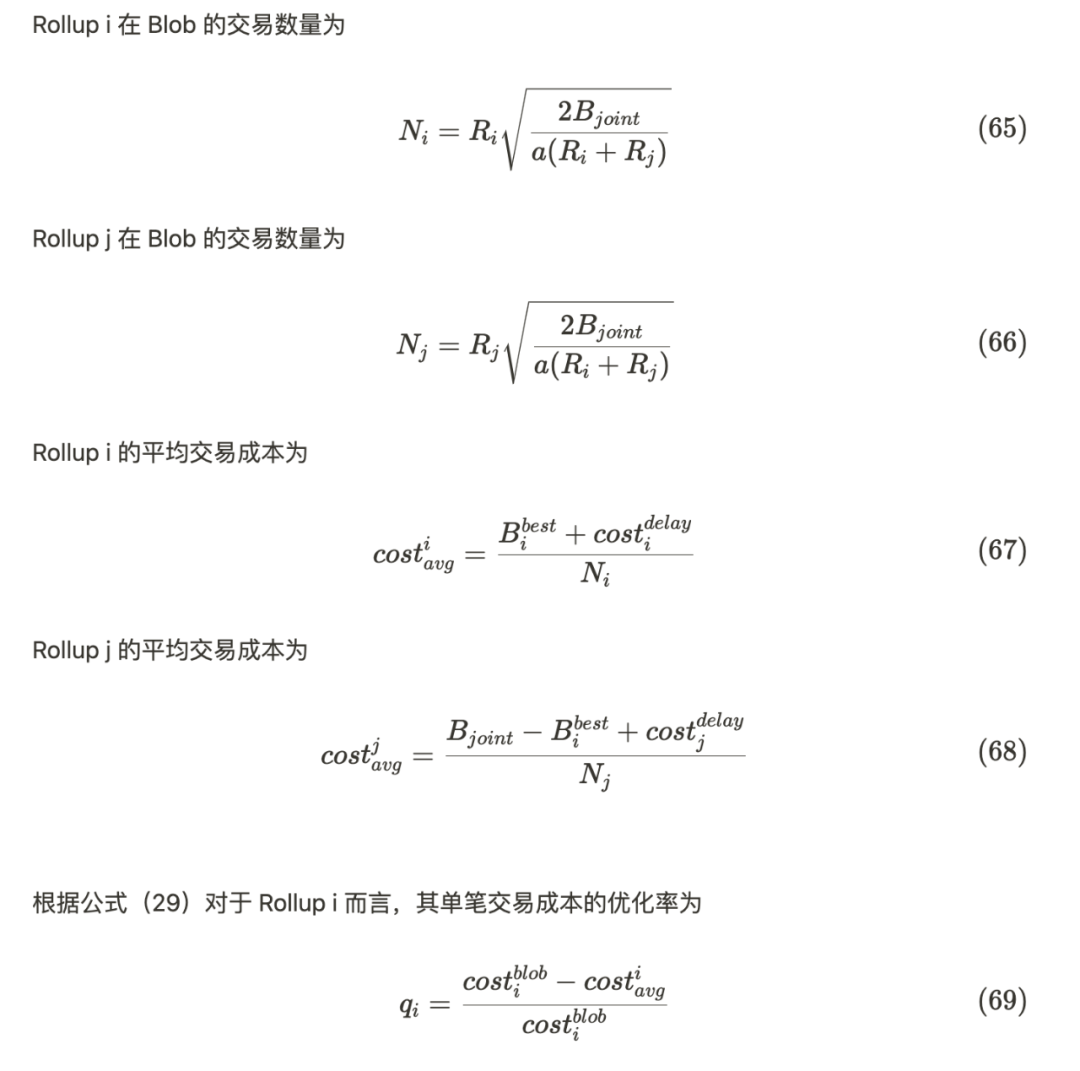

後記
EIP-4844 下Rollup 資料可用策略讓我們辯證地看待新舊技術,每種不同的技術都有其適用的範圍,我們需要劃清各個技術的效用邊界,從而讓我們更有效率地利用技術。延遲成本基本上主導了本文的推導,而這塊在平時的討論中都隱藏在水下。
後續仍有許多開放的研究空間,如限制Calldata 的EIP 敲定後,Rollup 資料可用策略會發生什麼變化。歡迎加入ETHconomics Research Space 一起討論研究。
相關資料
EIP 4844: What does it mean for L2 users?
https://medium.com/offchainlabs/eip-4844-what-does-it-mean-for-l2-users-5e86ebc4c028
EIP-4844 Economics and Rollup Strategies
https://arxiv.org/abs/2310.01155
EIP-4844 經濟學#1: 深入EIP-4844 費用機制


