作者:Vitalik Buterin,譯者:Kurt Pan,XPTY
本文假設你熟悉SNARK 和STARK 工作原理的基礎知識;如果你並不熟悉,建議閱讀此文的前幾節。特別感謝Eli ben-Sasson、Shahar Papini、Avihu Levy 和starkware 的其他人員提供的回饋和討論。
-
https://vitalik.eth.limo/general/2024/04/29/binius.html
-
https://en.wikipedia.org/wiki/Karatsuba_algorithm
-
https://polygon.technology/blog/plonky2-a-deep-dive
-
https://blog.icme.io/small-fields-for-zero-knowledge/
這一轉變已經使得證明速度大幅提升,最顯著的是Starkware 能夠在一台M3 的筆記型電腦上每秒證明620,000 個Poseidon2 哈希。具體來說這意味著,只要我們願意信任Poseidon2 作為雜湊函數的部分,那麼建立一個高效的ZK-EVM 中最困難的部分之一就已經得到了高效解決。但這些技術是如何運作的,密碼學證明(通常需要大整數來確保安全性)是如何在這些網域上建構的?而這些協議與更奇特的構造(如Binius)又如何比較?這篇文章將探討其中的一些微妙差別,會特別關註一種稱為Circle STARKs 的構造(在Starkware 的stwo、Polygon 的plonky3 和我自己的python 實現中有實現),其具有一些獨特的性質,旨在與高效率的Mersenne31 域相容。
-
https://x.com/StarkWareLtd/status/1807776563188162562
-
https://vitalik.eth.limo/general/2022/08/04/zkevm.html
-
https://vitalik.eth.limo/general/2024/04/29/binius.html
-
https://www.irreducible.com/posts/binius-hardware-optimized-snark
-
https://eprint.iacr.org/2024/278
-
https://github.com/starkware-libs/stwo
-
https://github.com/Plonky3/Plonky3
-
https://github.com/ethereum/research/tree/master/circlestark
小域常見的問題
在進行基於哈希的證明(或實際上任何類型的證明)時,最重要的「技巧」之一是用證明有關多項式在隨機點的求值以代替證明有關底層多項式的事情。

- https://en.wikipedia.org/wiki/Fiat%E2%80%93Shamir_heuristic

這個問題有兩個自然的解決方案:
- 執行多次隨機檢驗
- 擴域

- https://www2.clarku.edu/faculty/djoyce/complex/mult.html

這裡實現不是最優的(可以用Karatsuba優化),只是展示原理

常規FRI


- https://eccc.weizmann.ac.il/report/2017/134/

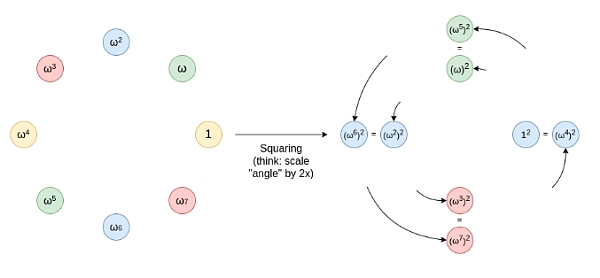

Circle FRI

- https://elibensasson.blog/why-im-excited-by-circle-stark-and-stwo/
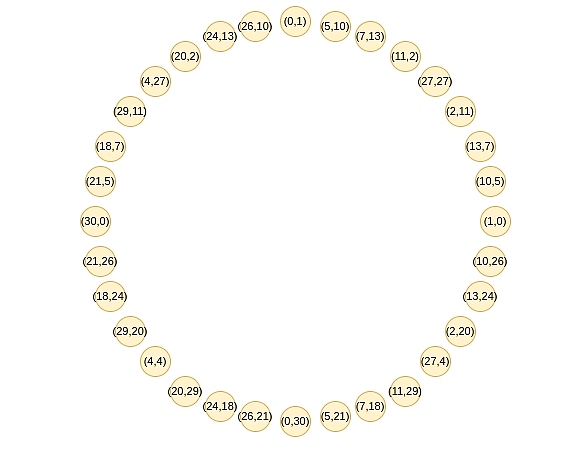
這些點遵循加法,如果你最近學過三角學或複數乘法,你可能會覺得這個定律很熟悉:
– https://unacademy.com/content/cbse-class-11/study-material/mathematics/algebra-of-complex-numbers-multiplication/

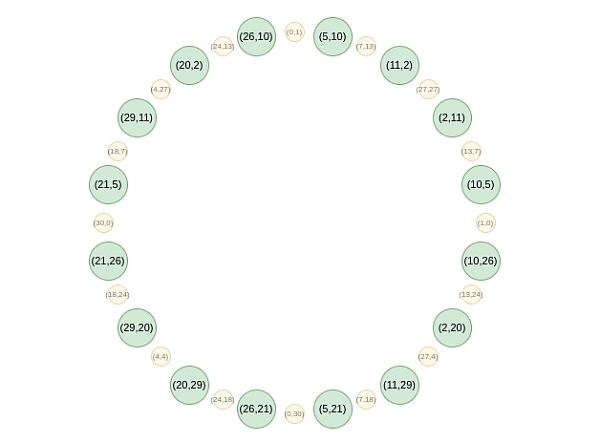

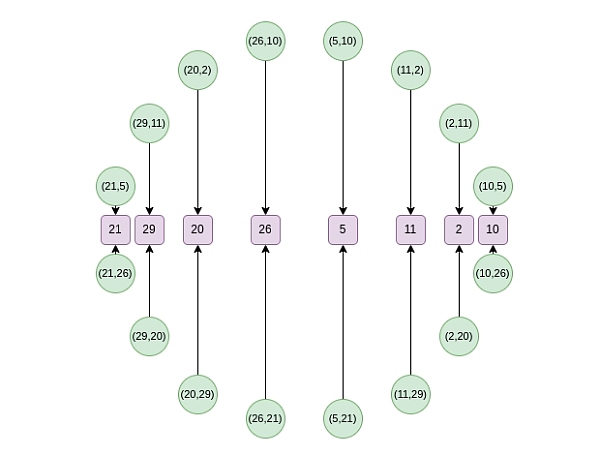
從第二輪往後,映射改變:

Circle FFTs

- https://vitalik.eth.limo/general/2019/05/12/fft.html


- https://www.researchgate.net/publication/353344649_Elliptic_Curve_Fast_Fourier_Transform_ECFFT_Part_I_Fast_Polynomial_Algorithms_over_all_Finite_Fields
從這裡開始,讓我們來了解一些更深奧的細節,對於實現circle STARK 的人來說,與常規STARK 相比,這些細節會有所不同。
取商

- https://eprint.iacr.org/2019/336


消失多項式

反轉比特序

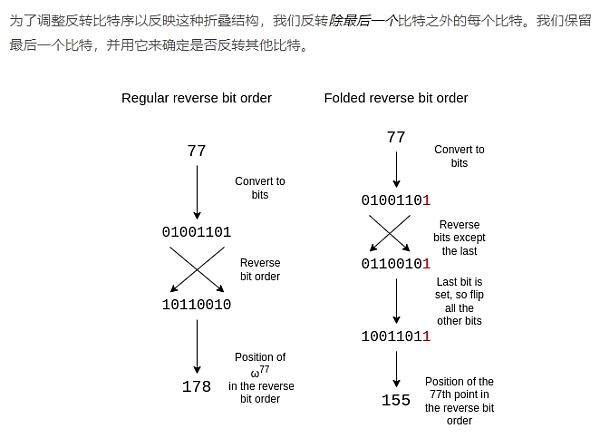

效率

因此,circle STARK 實際上非常接近最優了! Binius 甚至更強大,因為它允許混合搭配不同大小的域,從而為所有東西給出更高效的位元打包。 Binius 也提供了執行32 位元加法的選項,且無需產生查找表的開銷。然而,這些收益是以(在我看來)顯著更高的理論複雜性為代價的,而circle STARK(以及基於BabyBear 的常規STARK)在概念上是相當簡單的。
結論:我對circle STARKs 怎麼看?
與常規STARK 相比,Circle STARK 並不會為開發者帶來太多額外的複雜性。在實現的過程中,上述三個問題基本上就是我看到的與常規FRI 相比的唯一差異。 Circle FRI 所操作的「多項式」背後的數學原理是相當反直覺的,需要一段時間才能理解和領悟。但恰好這種複雜性被隱藏起來了使得開發者不會看到太多。 Circle 數學的複雜性是封裝過的,而不是系統性的。
-
https://vitalik.eth.limo/general/2022/02/28/complexity.html
理解circle FRI 和circle FFT 還是理解其他「奇異FFT」的良好智力途徑:最值得注意的是二進位域FFT,之前在Binius 和LibSTARK 中使用,還有更奇異的構造,如橢圓曲線FFT,其使用幾對一映射,可以很好地與橢圓曲線點運算一起使用。
-
https://github.com/ethereum/research/blob/master/binius/binary_ntt.py#L60
-
https://github.com/elibensasson/libSTARK
-
https://arxiv.org/abs/2107.08473
透過結合Mersenne31、BabyBear 和二進位域技術例如Binius,我們確實感覺得到正在接近STARK 「基礎層」效率的極限。在這個時間點,我預計STARK 優化的前沿將轉向對哈希函數和簽名等原語進行最高效的算術化(並為此目的優化這些原語本身)、進行遞歸構造以解鎖更多並行化、將虛擬機器進行算術化以提升開發者體驗,以及其他上層任務。


