本文總共分為中篇闡述自動做市商算法、現狀及未來迭代的思考,本文為中篇。下篇請點擊
目錄
7. Curve的StableSwap和交易公式
8. Curve V2 的動態權重、可定制的價格錨定和平滑的價格過渡
9. Curve V2 在2 代幣池中的做市商函數
10. 與CPMM 和StableSwap 相比,Curve V2 的價格函數
11. 價格重錨過程:Xcp 標準、EMA 價格預言機、相對價格變化步長 s
12. Curve V2的動態交易手續費
13. DEX聚合器:Balancer SOR算法的通用解決方案
14. Pivot 算法:解決無常損失問題的一種嘗試
15. 單邊流動性解決方案
Curve的StableSwap和交易公式:
Curve 將恆定加和做市商(CSMM) 和恆定乘積做市商(CPMM) 合併在一起,以實現更低的價格滑點。我們可以把這個算法看作是向Uniswap/Balancer 模型添加一個固定價格部分,使最終的做市函數錨定於一個價格。
Curve¹⁰ V1,被稱為StableSwap,設計了用於穩定幣交易的算法。它將CSMM 與權重相乘並加上CPMM:
曲線¹⁰ V1
StableSwap — 穩定幣流動性的有效機制
https://curve.fi/files/stableswap-paper.pdf
首先我們考慮一個特殊情況,即流動性池中每種代幣的數量是相同的。很容易證明在平衡點處時這個方程成立(χ 是權重,與Dⁿ⁻¹ 相乘以使CSMM 和CPMM 具有相同的數量級)。但是,當流動性池失衡時,如果χ 是一個常數,則該等式將不再成立。因此,我們需要將χ 變量化。 Curve V1 選擇了一種χ 的函數形式,使它在流動性池極端不平衡時變為零,這意味著該方程由CPMM 主導。在平衡點下,χ 等於A。 A 是一個常數,通過模擬歷史數據進行優化。代入χ 給了我們一個始終成立的方程。
接下來,讓我們推導出StableSwap 如何實際計算交易結果。根據當前池中的代幣數量,我們可以計算出D。例如,如果我們想換出代幣j,我們可以將xⱼ 分離開來並求解xⱼ 的方程:

該方程可以簡化為二次形式。可悲的是,現在鏈上Vyper語言裡沒有可以解二次方程的數學庫。因此,StableSwap 使用了牛頓法來求解xⱼ。迭代公式每次迭代都將其精度加倍。因此,可以在設定的gas上限內計算可接受的xⱼ。最後,交換前後xⱼ 之間的差值將是購買的代幣j 的數量。
牛頓法
它是一種在實數域和復數域上近似求解方程的方法
https://en.wikipedia.org/wiki/Newton%27s_method
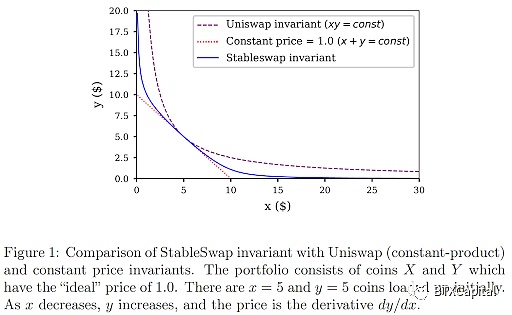
來自 StableSwap 白皮書
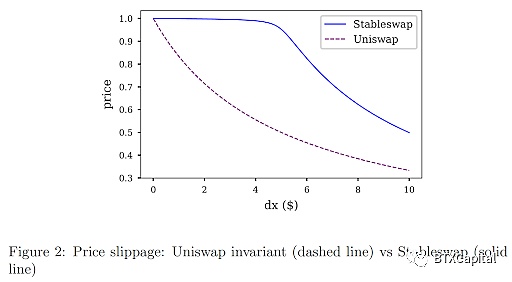
來自 StableSwap 白皮書
與CPMM 相比,StableSwap 做市商受壓、 以x + y = 常數方向壓平。這確保交易價格接近或等於1,在平衡點附近有非常小的滑點(當池中的一個代幣不接近幾乎售罄時)。當池中的一個代幣幾乎售罄時,價格開始急劇下降。這很容易理解:函數的曲率/滑點被集中/推到別處,以確保在平衡點附近的低滑點。
該模型中的CPMM 和動態權重被用於懲罰提前知道消息的大額訂單,防止池中的代幣被完全售罄。
優點:通過添加CSMM和CPMM以及動態權重,Curve的StableSwap 實現了非常小的滑點,非常適合穩定幣。
缺点:价格始终锚定在1。如果市场价格与流动性池价格显著不同,流动性池将被买空。因此,StableSwap 仅适用于稳定币。
Curve V2 的動態權重、可定制的價格錨定和平滑的價格過渡:
為了確保更平穩的價格過渡和可定制的價格錨定,Curve¹¹ V2 將動態權重χ 修改為K,如下所示:
曲線¹¹ V2
使用動態掛鉤自動做市
https://curve.fi/files/crypto-pools-paper.pdf

K0 在0(流動性池不平衡)和1(平衡點)之間變化,χ 和K(以A 歸一化)作為K0 的函數繪製如下:
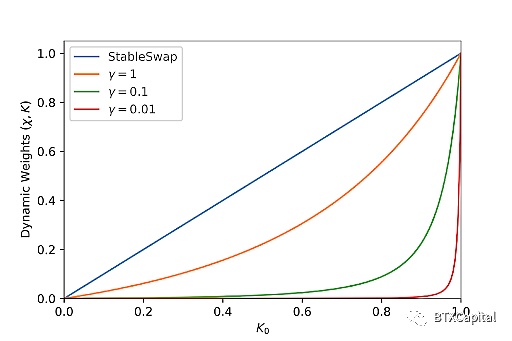
我們可以從上圖中了解Curve V2 如何使價格轉變得平滑。它實際上使動態權重在遠離平衡點時迅速下降。 γ值越小,下降越快。使動態權重快速下降到零本質上相當於強制函數表現得更像CPMM,即使流動性池只是有一點不平衡。
DW 在twitter¹² 上發布了一條很棒的推文,解釋了相同的概念。
DW 在 Twitter¹²的推文
1/ A general way to construct a @CurveFinance -esque curve, so you can make your own one.
The general form of the invariant:
(x+K) (y+K) = (s+K)^2
– s is the constant, a representation of pool liquidity
– K controls the curve's flatness pic.twitter.com/jLZ0yDoOes— DW (@dken_w) August 3, 2021
價格過渡問題得到了解決。現在我們討論Curve V2 如何實現其他不是1的價格錨定。有一個價格錨定(他們在白皮書中稱之為價格標度)意味著在做市曲線上存在一個平衡點,在平衡點處按價格標度縮放的代幣數量相等:

Curve V2 在2 代幣池中的做市商函數:
縮放後的代幣數滿足與StableSwap 類似的等式。以最簡單的2幣流動性池為例,做市商函數可以用A、γ、p、D、x、y 表示。該函數可以簡化為關於x, y 的三次函數(關於D 的六次函數)。
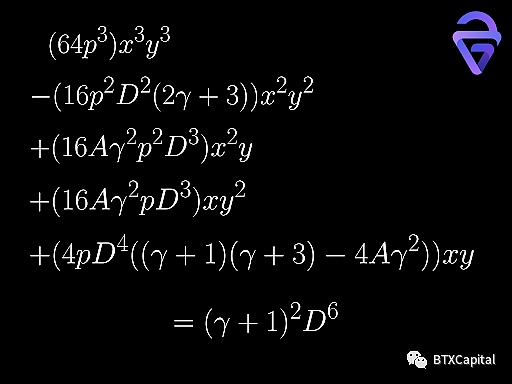
該函數的典型值圖如下所示:
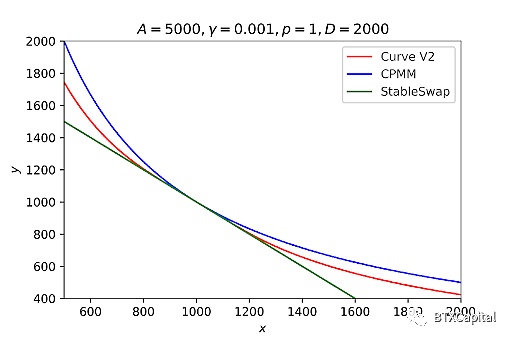
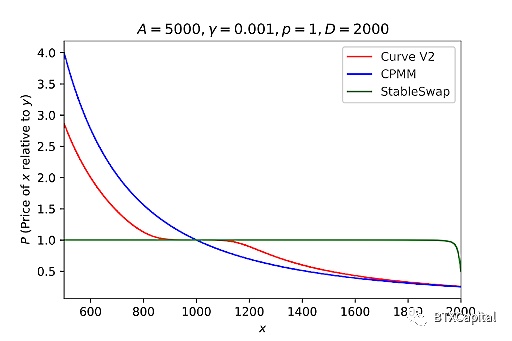
與CPMM和StableSwap相比,Curve V2的價格函數:
也可以繪製代幣x 相對於代幣y 的價格曲線。在平衡點(1000, 1000) 附近Curve V2 價格函數恆定。與StableSwap 相比,Curve V2 略微延遲了價格變動,而不是完全延遲。與CPMM 相比,隨著交易量的增加,價格開始以較小的滑點做出反應。總而言之,Curve V2 在平衡點附近實現了非常小的滑點,並且在其他區域比CPMM 實現了更好的滑點。至於其他非1的價格錨定,我們只需更改上面三次/六次方程中的p。因此,錨定價格的問題也解決了。
我們可以使用類似的在StableSwap中的牛頓法來計算交換結果。首先,我們根據池中當前的代幣數量計算D(這次使用牛頓法,因為方程要復雜得多)。其次,如果我們想換出代幣i,我們再次使用牛頓法來求解xᵢ。同樣,xᵢ的差異(按其價格標度歸一化)將是我購買的代幣數量(所有xᵢ 都是按價格標度縮放的代幣數量)。
為了確保多項式函數的根可以在設定的gas上限內求解,Curve白皮書討論了他們選擇的起始猜測,以及函數中的參數。他們使用一種稱為模糊測試(假設框架)的方法來確定這些最佳值。目前,我們不知道有關此方法的任何詳細信息,並且很想了解更多信息。
價格重錨過程:Xcp 標準、EMA 價格預言機、相對價格變化步長s:
為了確保小滑點(在平衡點附近交易), Curve V2通過改變價格標度不斷重錨做市商函數。然而,價格重錨可能導致流動性提供者承受價值損失。 Curve V2 引入了一個名為Xcp 的變量來緩解這個問題:
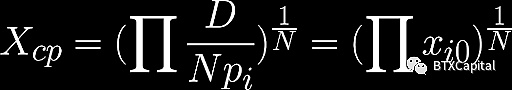
如果一次重錨後的損失大於累積的Xcp 的一半(原始Xcp 增加的價值),則該算法將保持做市商函數不變。有幾個問題我們想在未來回答,因為白皮書只簡要討論了Xcp。查看其源代碼可能會有所幫助。
-
Xcp 值是否與用流動性池中當前代幣數計算出的價值成正比?
-
存入或取出流動性是否計入Xcp?
-
如果取出流動性計入Xcp,如果Xcp減少幅度過大會阻止取出流動性嗎?
對於價格重錨,Curve V2 使用EMA(注:指數移動平均線)價格預言機來確定預言機價格。新的預言機價格向量由最近一次交易價格向量和前一個預言機價格向量的線性組合確定。新價格標度向量的變化方向與預言機價格相似,但不完全等於新預言機價格。他們通過引入相對價格變化步長s,將價格標度向量滯後於預言機價格。該方程可以使用歐幾里得幾何輕鬆導出。 EMA 價格預言機和價格標度延遲是為了減少近期價格波動的影響並更好地代表長期市場價格。

關於相對價格變化步長s,根據我們“刷新Curve官網”的經驗,部分流動性池的s 變化頻率至少為十分鐘的量級以上。 Curve V2 如何更新s 是一個有趣的問題,超出了我們當前知識的範圍。查看其源代碼也會有所幫助。
下面顯示了一個演示一次價格重錨過程的圖:
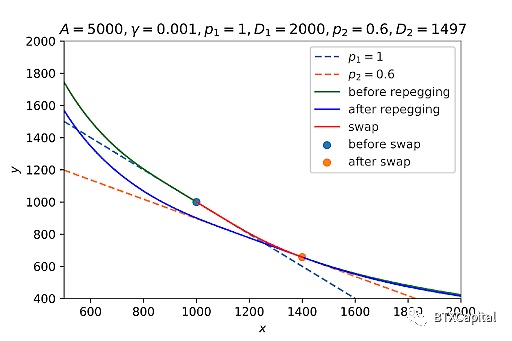
假設我們在x = 1000 開始我們的交易,並在x = 1400 結束我們的交易。最初,價格錨定於1 。交易後,價格移動到0.6。為簡化起見,僅出於演示目的,我們將新的價格標度設置為與現貨價格相等(價格現在錨定於0.6),並求解六次方程以獲得D。現在做市商函數錨定於0.6,如上所示。
價格重錨本質上相當於找到一個新的做市商函數,該函數穿過當前代幣數量位置(在2 代幣池情況下為(x, y)),在(x0, y0) 處有一個平衡點,使得y0/x0 為等於(x0, y0) 處導數的絕對值。一個有趣的課題是獲取真實的Curve流動性池參數,做一個更好的(可能是動畫)價格重錨過程的演示。
Curve V2的動態交易手續費:
由於上面討論的Curve V2 的做市商特性,將交易費用設為2級交易費用與動態權重的線性組合是合理的,衡量我們離平衡點有多遠(當前價格變動是否更像是StableSwap 或CPMM)。 Curve V2 選擇的fmid 和fout 值分別為0.04% 和0.4%。下圖展示了2 代幣池中的費用如何變化(假設沒有價格重錨或流動性變化):
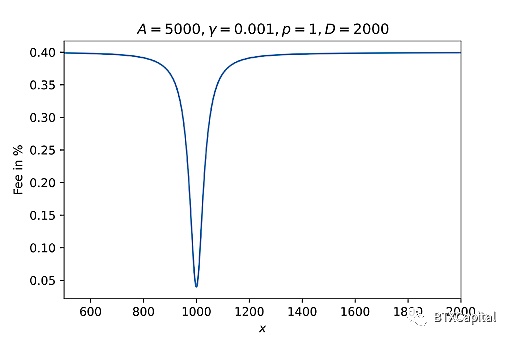
優點:做市商函數可以錨定於任何價格,適合所有代幣,而不僅僅是穩定幣。價格過渡比StableSwap 更平滑。 Curve V2還根據其內部的價格預言機不斷更新價格標度,以更好地代表市場價格,確保在平衡點附近交易。動態費用確保在此基礎上提供甚至更好的價格。
缺點:由於求解三次方程和六次方程,Gas 費用可能會更高。僅根據其內部價格預言機進行價格重錨可能存在風險。我們想知道在通過Xcp 標準時,是否存在價格標度與市場價格明顯不同的情況。如果是這種情況,與其他預言機交叉檢查價格可能會有所幫助。
Curve 的StableSwap 和動態錨定V2 是為了使交易滑點盡可能小。 StableSwap 始終錨定於1,而V2 使錨定價格跟隨市場價格。
下面將討論AMM 算法的一些最新進展和可能的改進。
DEX聚合器:Balancer SOR算法的通用解決方案:
DEX 聚合器是聚合現有AMM 協議以實現更好交易結果的協議。如上所述,Balancer 的SOR 算法也適用於DEX 聚合器,以確保數學上最優的交換策略。
Balancer 的SOR 算法的一般解決方案,沒有任何價格函數近似,可以表示如下:

因為價格函數可以是任何形式,具體取決於生成它們的AMM 算法。這意味著滿足總代幣數量守恆和相等最終價格等條件的方程可能沒有解析解。
因此,我們引入了一種在機器學習等領域常用的技術,稱為梯度下降。我們將損失函數定義為不同價格函數值的方差。在選擇一個起始猜測(一個簡單的、不知情的猜測可以是每個池中的交易量相等N/n)後,我們可以迭代(通過損失函數相對於該變量的偏導數改變每個交換量,乘以學習率l) 以獲得最佳結果,在一定的誤差接受範圍內。
由於作為最終等價函數的總交易量是單調的,因此該方法應該能夠找到全局最小值(方差= 0)。同樣,上面的計算假設沒有簡單的解決方案(沒有價格函數總是大於或小於範圍(0, N) 上的其餘價格函數)。
Pivot 算法:解決無常損失問題的一種嘗試:
Pivot 算法試圖通過使做市商函數經過一個固定點(x0, y0) 來對其進行樞軸旋轉。

(x0, y0) 處的價格將始終是設計的當前市場價格Pt。這在概念上確保套利總是將流動性池帶回到點(x0, y0)。由於此功能,無常損失將為零。然而,實際上,該算法沒有足夠的參數來擬合當前儲備(x,y)和(x0,y0)。這意味著我們必須等待流動性池回到(x0, y0),然後更改做市商函數。
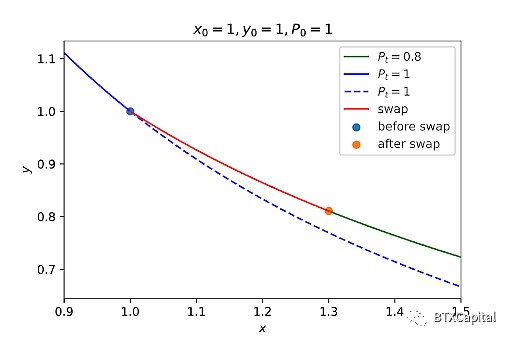
從上圖中我們可以看出,交易後的點不在新的做市商函數上(藍色和藍色虛線)。如果當前市場價格低於當前儲備的現貨價格,則流動性池也可能沒有任何動力回到(x0, y0)。
我們想知道是否存在這樣的函數通過(x, y) 和(x0, y0) 以及在(x0, y0) 處的可調導數來適應市場價格。如果我們假設函數是凸的,那麼市場價格不能小於這兩個點之間的線性段斜率。因此,如果做市商函數必須是凸函數,則此問題可能沒有完整的解決方案。
單邊流動性解決方案:
流動性提供者在存入流動性時可能不方便存入所有類型的資產。我想知道是否存在與Bancor 採取的彈性供應方法不同的其他機制。直覺上,有兩種解決方案:1. 首先使用相同的協議交換部分代幣2. 無論如何存入單邊流動性,讓套利將價格帶回市場價格。
例如,我們希望將流動性存入一個等值的2 代幣池中。

我們只有代幣x。不難計算我們需要交換多少,以便交換後每種代幣的價值相等。也很容易證明β 總是在0 和1 之間,這意味著一個合理的結果。但是,交易後的價格可能與存入流動性時的價格不同。因此,我想知道協議是否真的將交換和流動性存入作為一項原子操作。進行交易時也存在價格滑點。到目前為止,Balancer 和Curve 等協議如何處理單邊流動性存入仍然是我們的一個問題。如果滑點很小,則進行上述操作是合理的。
Balancer and Curve 白皮書中描述的第二種方法是是直接存入單邊流動性。這可能會大大改變價格。由此產生的套利也可能使無常損失變得重大。我們個人在Balancer 白皮書和文檔中沒有看到任何懲罰措施。另一方面,Curve 在存入單邊流動性時引入了一種稱為不平衡費的東西,其範圍從0% 到0.02%。在現實中,由於套利和無常損失,在第二種方法下存入單邊流動性並沒有真正的動機。
了解更多與單邊流動性相關的其他創新將會很有趣。
由於本論文過長, AMM 算法的一些最新進展和可能的改進及後續內容將於下篇公佈。
原文鏈接:https://link.medium.com/ynEydZUihjb
作者:Leo Liu, Guangwu Xie
翻譯:Vanessa Cao
校對:Leo Liu, Guangwu Xie
排版:Jane Hu
感謝:Fangyuan Zhao, Showen Peng, DW, Lianxuan Li, Dave White, Dan Robinson, Vanessa Cao, Jane Hu



