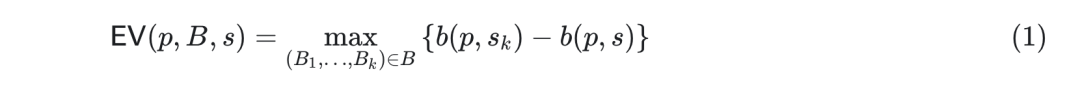然而,奇怪的是,對於MEV 的正式定義並沒有達成一致。
來源:Flashbots,感謝Phil Daian、Alex Obadia 和Mahimna Kelkar 就該主題進行了大量討論。原文標題《MEV的定義究竟是什麼? Flashbots進行了詳細解釋》
自從Daian 等人在2019 年的Flashboys 2.0 論文中引入礦工可提取價值(MEV)(也就是現在的最大可提取價值)以來,關於MEV的討論已經很多。特別是,Flashbots Auction的推出推動了當今跨越各種區塊鍊和中心化交易所的十億美元經濟。從激動人心的Twitter 話題到學術研究論文,MEV 現像已成為加密貨幣討論的核心。然而,奇怪的是,對於MEV 的正式定義並沒有達成一致。
雖然有些人可能會爭辯說,在大多數情況下,廣泛共享的、直觀的MEV 概念就足夠了,但我們認為,適當的正式化對於建立可以進行複雜理論化的基礎至關重要。正如Tim Roughgarden 在最近一次關於構建DeFi 理論的演講中所說的那樣,在“簡單”和後來的“困難”定理之前,第一步是要有定義和基本詞彙。此外,正如最近的公開討論所證明的那樣,有些人聲稱套利不是MEV,甚至可能是我們根本不共享MEV 的直觀概念!一個統一正式的MEV 定義肯定會有所幫助。
然而,事實證明,以穩健、通用的方式正式化MEV 並非易事。在這篇文章中,我們探討了在嘗試提出這樣一個定義時遇到的一些困難。我們首先回顧一些現有的正式化,指出它們的一些問題,並繼續尋求對其中一些進行修正。雖然我們提出了改進其中一些問題的新定義,但我們的主要貢獻在於突出了所涉及的許多微妙之處,為未來圍繞MEV 的工作採用更系統的方法鋪平了道路。
1
當前MEV 定義
最初的Flashboys 論文將MEV 定義為“在給定時間範圍內,以太坊礦工可以從交易操縱中提取的總量,其中可能包括多個區塊的交易價值”,但沒有嘗試正式定義。最近,廣泛採用的工作定義類似於:
MEV 是區塊提議者可以通過重新排序、審查或插入交易而無需許可地提取的價值。
也許最接近正式化的定義是最近的Clockwork Finance 論文中通過以下兩個表達式給出的定義:
和:
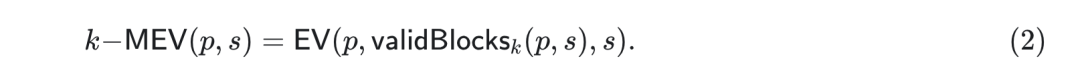
這裡,EV 是在給定一組有效區塊序列B 的情況下,玩家p 在狀態s 中可提取的價值,(B1 ,…,Bn ) 就是這樣的一個序列,而b(p,Sk ) 是玩家p 的餘額在將區塊(B1 ,…,Bk ) 應用於s 後的狀態。 k-MEV 是處於狀態s 的玩家p 作為區塊提議者的k-最大可提取值,其中validBlocksk 是p 可以創建的k 個區塊的所有有效區塊序列的集合,而單區塊MEV 僅為1-MEV。
為了記數簡單性,這些表達式與論文中的表達式略有調整,但在其他方面是等效的。特別是,我們考慮玩家的餘額而不是賬戶(省略玩家控制的賬戶的總和),並刪除對鏈的原生資產的顯式引用;稍後我們將回到這一點。
我們將使用MEV 的這個定義作為起點,並註意到大多數其他論文提供了面臨相同限制的類似定義,或者根本不提供正式定義。
2
現存的限制
我們首先註意到上述表達式中的一個致命缺陷:最大可提取值(MEV)取決於玩家p!這意味著如果p 有一些待處理的空投領取,他們的MEV 將大於沒有的玩家。雖然這對於可提取值可能有意義,但它肯定與“無許可提取”價值的想法不一致。
仔細檢查後,並不完全清楚“玩家”的概念實際上指的是什麼。我們可以確定至少三個相互交織的含義:i) 作為交易簽名者的玩家,擁有餘額和控制賬戶,ii) 作為協議遊戲中的參與者,擁有(或缺乏)區塊提議權,以及iii) 網絡意義上的玩家,受延遲影響並擁有獨特內存池視圖的節點運營商。
雖然後一種含義可能不適用於這個公式,但含義i) 和ii) 有點混淆:p 在談論(1) 中的餘額時肯定指的是i),但在從(1)到(2),我們還賦予了p 區塊提議權,符合含義ii)。我們認為MEV 的正確定義應該獨立於i) 意義上的玩家,也就是說,它不應該依賴於特定的簽約權。關於ii),我們將定義給定區塊提議權限的MEV。這有效地將問題一方面解耦為價值提取,另一方面獲得排序權,這在考慮提取成本、網絡安全等時可能會很有用。
上述定義的其他注意事項是對多區塊MEV 的處理(與上述i) 和ii) 含義的糾纏有關)、因撤回交易而產生的費用的遺漏,以及試圖將MEV 推廣到跨域設置時區塊概念的不足。在接下來的內容中,我們嘗試修補定義以在可能的情況下解決其中的一些問題,並討論我們在此過程中發現的一些其他困難。
3
修補MEV
如上所述,首要任務是提出一個真正無需許可的MEV 定義。我們將在可提取值的定義中保留玩家依賴性,但在移動到MEV 時擺脫它。我們在這裡註意到,我們在上面i) 的意義上使用player,賦予它對EV 和MEV 的完整區塊排序權限。我們提出以下建議:
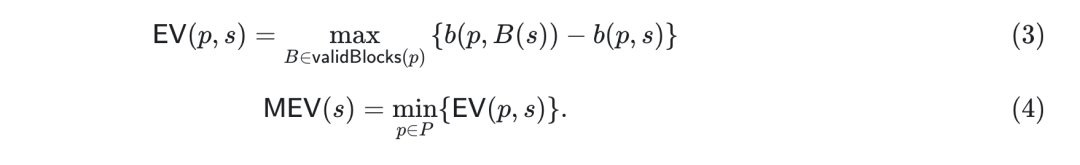
這裡的第一個表達式與(1) 非常相似,但我們刪除了對有效區塊序列集的依賴,這是隱式的,我們只考慮單個塊(稍後會詳細介紹)。這裡的validBlocks(p)是p可以提出的有效區塊的集合(validBlocks1 (p,s)之前,為了簡潔省略了區塊的數量和狀態依賴)。 B(s) 反過來表示通過在狀態s 之上應用區塊B 獲得的狀態。
在表達式(4) 中,我們獲得了MEV 的定義,根據需要,該定義獨立於玩家(表示P 玩家集)。雖然在最大可提取值的定義中找到最小值可能有悖常理,但這個最小值只是編碼了提取應該是無許可的想法。 EV 已經負責最大化,無需許可即可提取的價值是特權最低的參與者可以從網絡中獲取的價值(同樣,假設他們擁有區塊提議權)。
然而,這個定義引出了一個問題,當挖礦需要前期資本時會發生什麼?定義(2) 沒有這個問題,因為它對玩家有明確的依賴,但是現在刪除了它,我們需要考慮到某些MEV 可能只能在某些初始資本水平下才能提取。然而,我們注意到gas 費用不是這裡要求的一部分,因為提議者可以隨意排序“免費”交易,因此即使沒有初始資本,通常MEV 也可能大於零。
儘管如此,我們希望明確對資本的依賴,因為許多MEV 機會都依賴於它。我們寫(使用(3)中的EV):
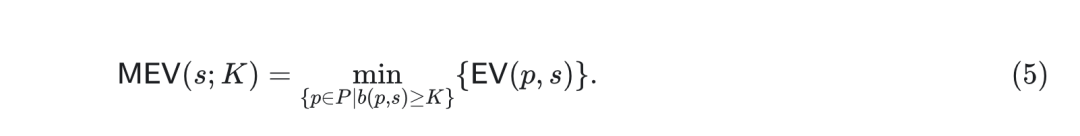
這個定義告訴我們,狀態s 中初始資本K 的最大可提取價值是任何至少擁有該數量初始資本的玩家可以提取的價值。
我們考慮的下一步是內存池中的交易會發生什麼。在上面我們考慮了“有效區塊”,但至關重要的是,這些可以包含已撤回的交易,即支付費用,但不修改狀態。這是一個棘手的問題,因為它涉及上面的含義iii) 對玩家來說,因為內存池的不同視圖會產生不同的有效區塊集。雖然在實踐中提取MEV 的搜索者不斷在內存池中尋找機會,但交易最終需要包含在一個區塊中以修改狀態並產生機會,因此如果我們在有效交易方面不失一般性只考慮狀態變化,而不是更一般的有效塊概念。在這種情況下,我們確實丟失了作為MEV 來源的撤回交易,因此我們可以嘗試修改我們的公式以包含依賴於玩家的內存池的視圖,但這會混淆i) 和iii) 的含義,並且我們會遇到最小化過度玩家時的麻煩。考慮到內存池架構僅針對某些領域,這也會限製表達式的泛化性。因此,我們明確排除了作為MEV 來源的撤回交易,但請注意,它們是排序器帶回的收入的一部分,並有助於MEV 提取的負外部性,如可提取價值成本所量化。
省略撤回交易使我們能夠走得更遠,超越區塊的概念,這將使我們能夠在更一般的領域(如中心化交易所)中考慮MEV。我們將可提取價值的定義重寫為:
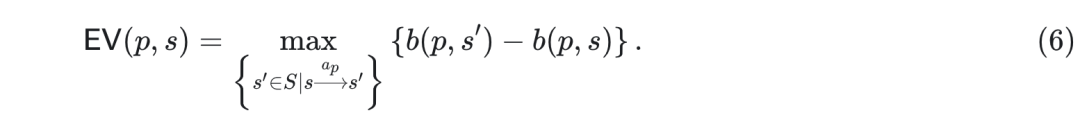
這裡,S 是所有狀態的集合,符號Sap S’ 表示狀態S’ 可以通過玩家p 的某個動作或動作序列ap 從狀態s 到達。與上面的等式(5) 一起,我們獲得了可以輕鬆推廣到跨域情況的定義(見下文),並解決了我們在定義(1) 和(2) 中遇到的大多數問題。
4
懸而未決的問題和擴展
在修補MEV 定義時,我們轉向了單區塊,徹底解決了多區塊MEV 的問題。事實上,我們最新的表達式(5) 和(6) 會自動考慮到這一點,因為通過根據狀態而不是區塊來表達EV,這些公式適用於提議者擁有排序權的任何時期。現在的問題成為如何獲得這些訂購權的方法之一。為了乾淨利落地做到這一點,我們需要歸因於不同事件的概率(比如產生單個區塊、兩個連續區塊等),這樣我們就可以得出總MEV 的預期值。然而,這超出了MEV 形式化的範圍,因為一旦定義了足夠的集成,就可以簡單地插入表達式(5)。
我們順便提到的另一個話題是跨域MEV。在一個不同鏈(或更一般的域)有自己的狀態更新機制,但通過其狀態中的依賴關係有效鏈接的世界中(想想L1 存款在處理時會影響L2 餘額),我們希望找到MEV,它只能是通過對多個域中的狀態變化進行排序來提取。我們在狀態方面的表述適用於這種擴展,但需要注意的是,不同的域具有不同的本地資產,我們需要考慮到這一點。我們不會在這裡詳細介紹,但是可以通過引入定價功能來解決這個問題,以便從一個域轉換到另一個域。首先近似,我們可以取一個定價函數pi→j 從域i 的本地資產到域j 的資產,並要求pj→i =1/pi→j 。更現實的是,我們預計價格是許多因素的玩家依賴函數,如不同域的不同資產數量、域的信任假設等。
我們注意到,自始至終,我們都將EV 和MEV 視為玩家的收入,從未考慮過成本。這與我們對具有給定訂購權的玩家的定義相吻合,因為獲得這些權利可以說是MEV 提取中成本最高的組成部分(儘管考慮到訂購問題是一個NP 完全背包問題,計算成本可能並不重要)。無論如何,將MEV 僅視為收入組成部分並單獨考慮提取成本似乎更清晰。就像在多區塊設置中一樣,我們可以定義一個概率集成來獲得排序權,並考慮與每個概率分佈相關的成本。然而,更棘手的是,排序權限通常以每個域的特徵為單位授予(例如,提議一個區塊),而成本通常表示為費率(每單位時間)。因此,雖然MEV 通常以區塊形式出現,但生產這些區塊的成本將以時間單位表示,並且它們之間的關係的細節將因每個域而異。每個域如何實現最終確定對於建立這種關係也至關重要(也許1 年前有一個很好的MEV 機會,但重新組織鏈以獲得它的成本會令人望而卻步),所以我們不期望有一種MEV 的通用公式來適應它。
最後,我們只考慮了“確定的”MEV,用狀態改變後增加的餘額來表達它(MEV 為正)。這不足以描述更一般的“概率MEV”概念,在這種概念中,玩家願意承擔風險以期獲得以後的回報。這方面的例子是在預期價格上漲時買斷新的代幣清單,或者搶跑NFT 出價。很可能這些機會中的大部分都可以通過合併定價函數來描述,我們期待看到朝這個方向發展的工作。
5
結論
MEV興起需要一種一致的正式方法來解鎖正確的理論(例如,以智能合約系統的MEV 暴露的自動審計為例,與上面引用的Clockwork Finance 論文中的工作一致)。然而,正式化MEV 涉及大量的技術細節,這些技術細節通常會為了完整性而權衡通用性(例如是否包括撤回交易的情況)。在這裡,我們為參與者的概念提供了明確的含義,這使我們將獲得排序權的問題與價值提取的問題分開,使我們能夠在定義MEV 時具有很大的普遍性。我們的公式(5) 和(6) 提供了一個一致的、易於推廣的定義,可以用於多領域世界。我們還強調了在實現MEV 的正式定義時面臨的許多問題,我們希望這些問題能夠更系統地處理該主題。
展開全文打開碳鏈價值APP 查看更多精彩資訊