作者:Frogs Anonymous,本文由DeFi 之道編譯
當今市場上不乏DeFi 協議,並且有大量機會通過為它們提供流動性來賺取收益。 UniSwap、Balancer 和Curve 等“老牌”協議,開創了現在幾乎所有AMM 協議都使用的恆定乘積做市商(Constant Product Market Maker,CPMM)模型和StableSwap 不變量。他們的主張很簡單:用戶提供流動性,當池子被用來交易時,每個協議根據這些公式分配費用。
然而,使用這些不變量的LP 會注意到一個關鍵問題:價格變化會導致損失,而費用一般無法彌補。這種利潤損失——無形的,但可衡量的,被稱為無常損失。那麼,當你可以通過簡單的持有和出售獲得更多收益時,為什麼還要提供流動性呢?
如果我們能改變這個想法,讓自己從這種最初的損失中獲利呢?如果我們能夠利用這一現象,在更廣泛的多/空策略中作為一個有利可圖的對沖呢?
這一切都可以通過我稱之為“LP Diving”的技術來實現。為了更好地理解它,讓我們先回顧一下無常損失的基礎知識。
無常損失
無常損失是一個相當簡單的概念,但其含義是可怕的:持有和出售資產比將其部署在流動性池中並收取費用更具收益性。這是因為兩個池子裡的資產之間的價格差異造成了損失。那麼,無常損失更準確地描述為差異損失(Divergence Loss)。
以LP 池K 中的兩種資產為例,它們的可變價格升值不受AMM/LP 本身的影響。想像一下,你投入了:
-
500 個代幣A,價格為1 美元
-
500 個代幣B,價格為1 美元
-
以1000 美元的價格存入1000 個代幣
現在,考慮一種情況:
-
代幣A 從1 美元增加到5 美元(增加500%)
-
代幣B 從1 美元增加到2 美元(增加200%)
-
最終價值為3500 美元
合理的假設是,存款人以後可以在價格升值或貶值後以1:1 的比例提取存款,就像買入並持有一樣。 500 個代幣A,500 個代幣B。
但是,這不會發生。這個池被指示根據預言機價格以及每當交易通過它們進行做市。因此它的名字——恆定乘積做市商。
除非兩種資產有足夠強的相關性,以至於每種資產的價格delta 相等,否則每當價格出現分歧時,儲戶就會提取不規則的數量。實際上,存款人將提取:
-
316.23 個代幣A,價值1581.14 美元
-
790.57 個代幣B,價值1581.14 美元
-
如果存入,最終價值為3162.28 美元
存款人經歷9.65% 的無常損失(或比持有時少337.72 美元)。
A.1 – 持有與提供(價格)的對比
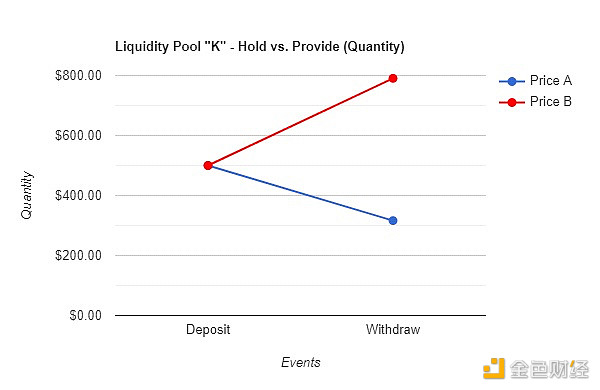
A.2 – 持有與提供(數量)的比較
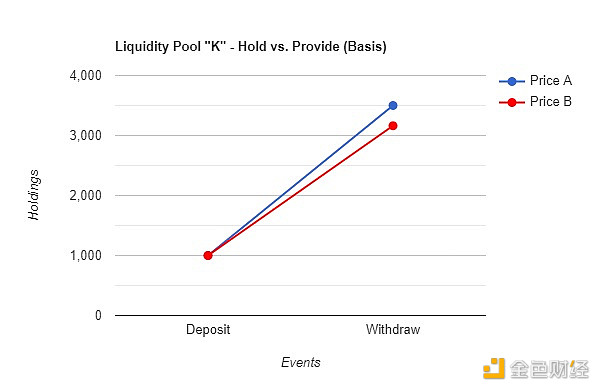
A.3 – 持有與提供(價值基礎)的對比
這個利潤明顯低於完全不提供流動性所能獲得的利潤,這往往會使池子裡的存款人首先不願意存款。許多協議試圖通過發放(代幣)來激勵流動性,作為向儲戶支付費用的一種方式,但這些費用幾乎總是不能彌補價格差異帶來的損失。
考慮一下:協議是否有能力向每個存款人支付差價——在上面的例子中是337.72 美元?通常情況下,作為費用支付的代幣通過分配膨脹的低成本供應來補償,這通常會迫使儲戶簡單地重新復合所賺取的邊際利潤。對無常損失的受害者來說,這是個小小的安慰!
顛覆想法
這就是為什麼不鼓勵將超過一種資產集中在一起的核心原因——它增加了做市商的複雜性。此外,根據利潤不斷地重新分配資產,使得儲戶很難預測他們是否能通過領取LP 代幣來拿回他們的錢。
然而,在觀察AMM 行為時可以看到一個獨特的價值記錄。再看看我們前面提到的例子的結果。
-
316.23 個代幣A,價值1581.14 美元
-
790.57 個代幣B,價值1581.14 美元
請注意,雖然A 和B 的價格相同,但提取的代幣數量不同。我們從500 個代幣B 開始,現在有790.57 個。自動做市商的效果是存款人用A 的股份換B 的股份,而這兩種資產的價格都會隨著時間的推移而上漲。隨著它們之間的價格出現分歧,我們利用我們對A 的分配,將更多的股份分配給B。
那些從事流動性池工作的人可以應用一種更複雜的方法,通過利用重新分配機制,從基於CPMM 的LP 中獲利,我稱之為“LP Dive”的一種相互作用。
初學者的高級流動性
這個概念相當簡單:將資金存入流動性池,然後在價格出現分歧時提取資產。然後,為數量較多的資產建立一個多頭頭寸。
盈利的跳水(Dive)源於利用差異損失的現象。核心押注是,在分歧之後,多頭資產頭寸的升值速度是指數化的,收益大於持有或存款。對於常見的代幣LP 設置,本文提供了兩個例子:代幣穩定池的Compression Dive,以及Token-Token Pool 的Twin Dive。
示例一:代幣穩定礦池跳水
代幣穩定池的工作方式就像一個原生的美元成本平均機制,在任何方向都是如此。這是對沖的核心——存入代幣穩定池允許用戶在上升或下降的過程中以較低的收益進行DCA(美元成本平均),同時賺取一些費用。這將被稱為壓縮跳水(Compression Dive)。
讓我們來看看這個例子。假設投資者LP 具有:
-
500 個代幣A 和500 個穩定幣B,每人1 美元購買(押金1000 美元)
-
該投資者使用靈活的多/空策略
-
投資者做多A,靈活做空 B
然後,假設發生以下情況:
-
代幣A 的價格降至0.01 美元
-
穩定幣B 的價格保持在1 美元
由於投資者希望在A 上持有一個多頭頭寸,因此如果價格貶值,他們可以簡單地撤回其流動性池代幣K。在此示例中,當代幣A 達到0.01 美元的價格點時,投資者退出,留下5000 代幣A 和50 個穩定幣B。
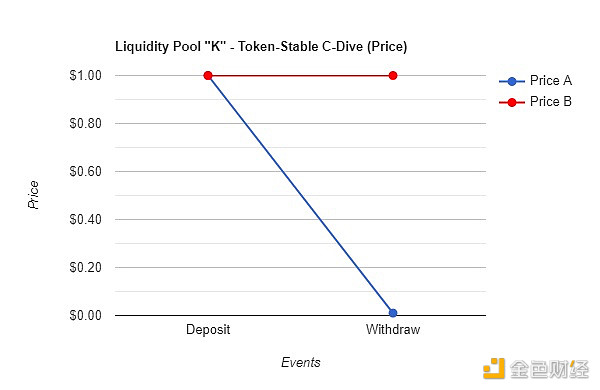
D.1 – 壓縮跳水價格變化
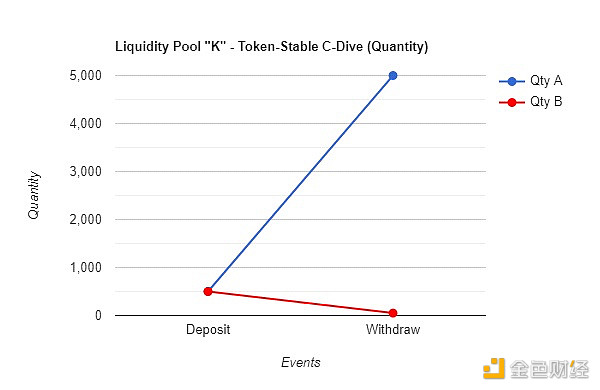
D.2 – 壓縮跳水數量的變化
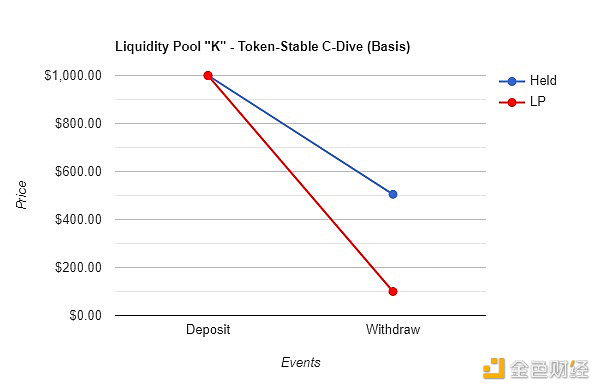
D.3 – 壓縮跳水基礎變化
其結果是存款人的損失增加了!
LP’ing 給他們總共剩下了100 美元,而如果他們簡單地持有,他們會有505 美元。對於流動性池的儲戶來說,這似乎是一個相當糟糕的情況,因為應計費用不能補償這種程度的損失。
在這個例子中,無常損失被計算為80.2%,如果儲戶沒有監控他們的頭寸,淨損失非常大!存款人損失慘重,他們可能會傾向於割肉。
這就是我們在這個流動性資金池中“跳水”的地方。即使池子的價格(可索賠的存款)下降了,A 的數量還是呈指數增長。無論他們知道與否,隨著價格的下降,儲戶用他們的穩定幣B 購買了更多的A。
這裡LP 跳水的核心前提是:將無常損失重新規劃為對代幣的重新分配,相信它們會回到初始價格。投資者沒有放棄代幣A 的頭寸,而是退出以持有多頭頭寸。通過持有這個多頭頭寸,投資者實際上降低了他們的盈虧平衡價格!
-
存款人擁有5000 個代幣 A
-
存款人有850 美元的無常損失(損失900 美元–剩餘的50 美元來自穩定幣B)
-
用無常損失(IL)除以代幣A 的數量(850/5000)
-
當代幣A 價格= 0.17 美元時,儲戶收支平衡
這就是指數收益發生的地方。在這個例子中,當代幣A 升值超過0.17 美元時,多頭頭寸的風險回報率也會呈指數級增長。
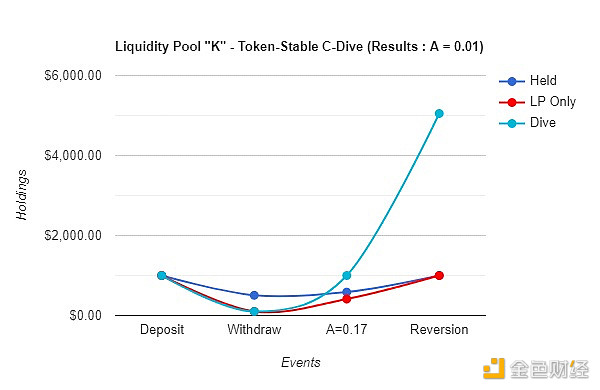
D.4 – A = 0.01 美元時的壓縮跳水回歸比較
這個時候,精明的觀察者可能會考慮在沒有流動資金池的情況下採用這種策略:他們不再存入1000 美元,而是簡單地使用初始1000 美元的一半或全部以0.01 美元的折扣價購買100000 個代幣A。這種策略在沒有LP 的情況下表現更好,因為交易者在沒有額外工具的情況下做市。
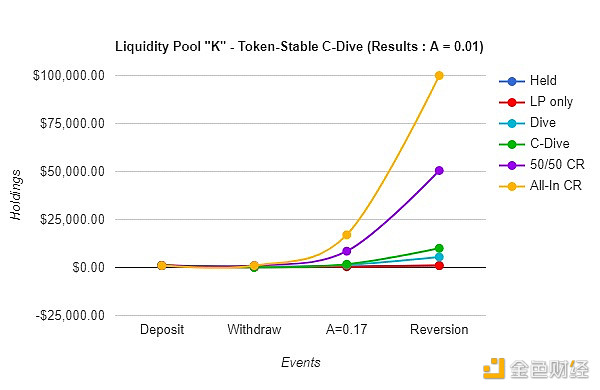
D.5 – 50/50 或All-In Pico 底部交易的壓縮跳水回歸比較
這就引出了一個問題:當確定Pico 底部是最賺錢的時候,為什麼還要使用跳水策略呢?這個想法是,使用跳水策略允許投資者在功能上使用LP 作為對沖工具。下行風險通過AMM 的機制自然得到保護,因為確定Pico 底部的時機說起來容易,做起來難。
通過整合來壓縮代幣價格以獲得收益
我們可以通過借鑒底部做市商的思路,並在跳水策略中實施來重新平衡風險配置。那麼,壓縮就是行使靈活的空頭頭寸。
跳水者可以選擇在他們立即撤出後鞏固他們的穩定幣B 頭寸,以現貨價格買入代幣A。在恢復到初始價格的前提下,這進一步放大了跳水策略的收益。
總結:
-
使用50 個穩定幣B 增加5000 個代幣A 的頭寸
-
存款人現在有10000 個代幣 A
-
我們仍然假設這是一個不使用集中流動性頭寸的LP
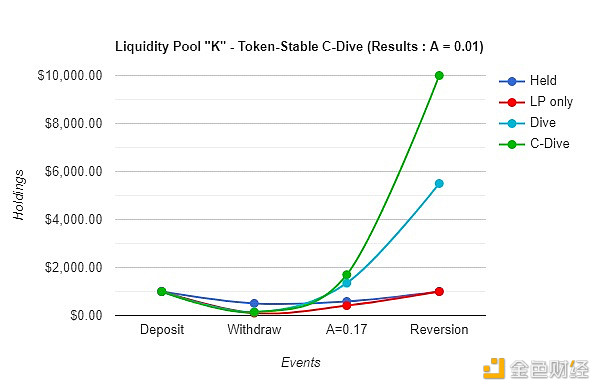
D.6 – 壓縮跳水的槓桿作用示例
這是C-Dive 最吸引人的地方:最終的總頭寸為10000 美元,初始存款後有9000 美元利潤。在流動性池上使用壓縮跳水策略,可以對代幣A 的頭寸進行原生對沖,並獲得類似於選擇本地或pico 底部的利潤。
示例二:Token-Token Pool Dive
真正神奇的是當你開始處理兩個具有波動性的代幣時。如果使用得當,LP 會你最喜歡的對沖工具。使用Token-Token Pool 開始引入槓桿跳水策略,通過將一種資產與另一種資產壓縮,以獲得成倍的收益。
讓我們假設一個投資者的投入與以前相同:
-
500 個代幣A,500 個代幣B——每個1 美元
-
1000 美元的初始存款
-
該投資者使用靈活的多/空策略
-
該投資者做多A,靈活做空 B
然後,假設發生以下情況:
-
代幣A 的價格降至0.01 美元
-
代幣B 的價格上漲至2 美元
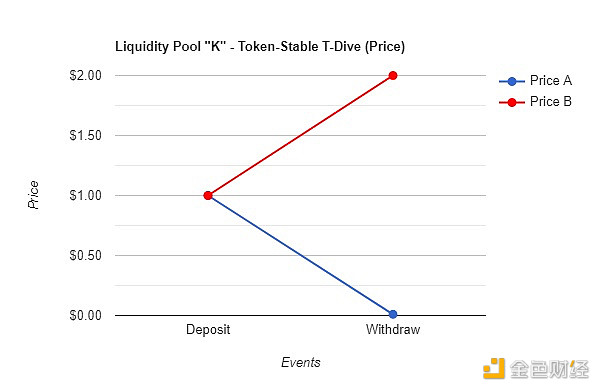
E.1 – Twin-Dive 價格變化
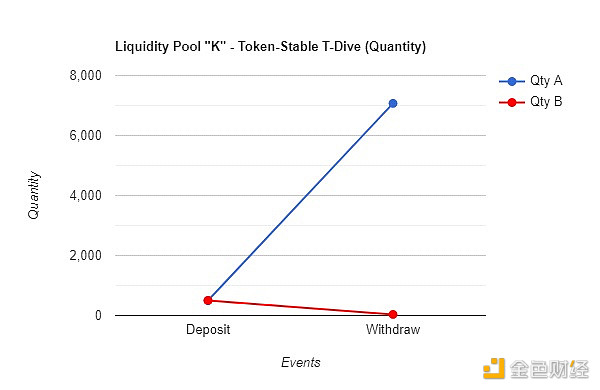
E.2 – Twin-Dive 數量變化
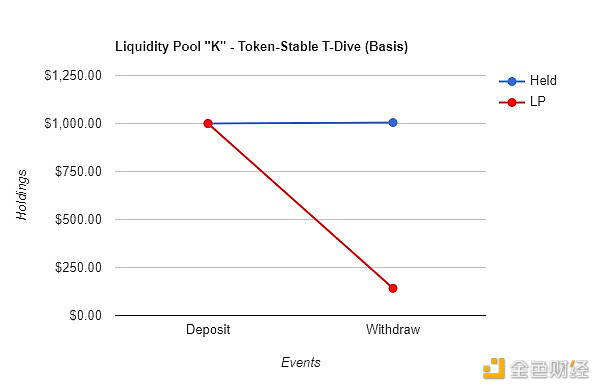
E.3 – Twin-Dive 基礎變化
跳水退出總結:
-
7071.07 代幣 A
-
35.36 代幣 B
-
如果持有,價值1005 美元
-
如果存放在LP 中,則為141.42 美元
在這種情況下,無常損失計算為85.93% – 比Token-Stable 池的IL 高5.73%!從這個角度來看,差異損失看起來非常可怕。
讓我們評估盈虧平衡點:
-
7071.07 的代幣A 需要補償初始存款的- 858.58 美元的損失
-
存款人擁有35.36 個代幣B,即70.72 美元
-
我們必須補償代幣B 在回升過程中的定量IL 損失(也就是用Token),以計算收支平衡
-
我們從存款價值中減去代幣B 持有量(1000 – 70.72)
-
將此IL 補償值除以代幣A 的數量(929.28/7071.07)
-
當代幣A = ~0.13142 美元時,存款人達到盈虧平衡
此外,儲戶可以通過事後立即買入來選擇是否在取款時行使空頭頭寸。我們可以像在最初的壓縮跳水法中那樣,在提款時取B 的價值,並以此為槓桿。這使我們的代幣持有量增加了一倍,達到14,143.07。
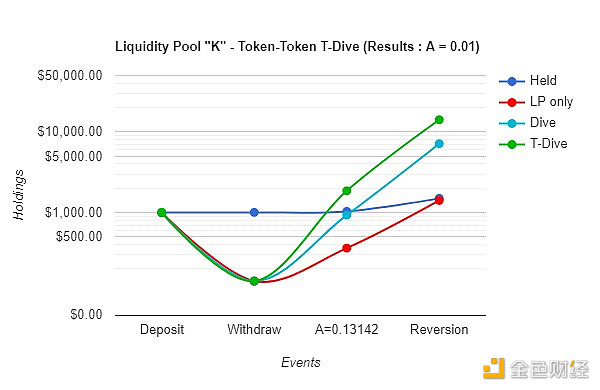
E.4 – A = 0.01 時的壓縮跳水回歸比較- 使用A = 0.13142 作為盈虧平衡點(對數刻度)
正如人們開始看到的那樣,使用Twin Dive 是根據B 的槓桿購買力利用壓縮跳水的一種槓桿形式。這是在Token-Token Pool 上使用跳水方法的嚴格好處。計算Token-Token 雙跳水策略上可用的基本槓桿的最簡單方法是,將槓桿代幣或代幣B,在這種情況下,將其除以代幣A 的價格。
例如:
-
代幣B 在提款時的價格為2 美元
-
代幣A 的提款價格為0.01 美元
-
基本槓桿為200
這種策略通常被稱為流動性“吸血鬼”。這是因為流動性通過代幣數量有效地從儲戶那裡獲取,並根據槓桿率轉移給跳水者。一般來說,這種流動性是根據其MEV 提取的,也就是說它是一種有效的做空工具。
LP Dive 的積極和消極影響
假設價格預測有利於多頭/空頭投資者的方法,並且收費收益代幣具有價值,那麼使用跳水方法可以減輕無常的損失,並將利潤複利給存款人。任何投資者都可以在任何利用CPMM 不變量的LP 上使用這一策略,或其一些衍生品(包括StableSwap)。在集中的LP 頭寸上使用這種方法有額外的細微差別,一般效果因個人協議而異。
與簡單的買入、持有和賣出相比,相對於協議功能允許的標準行為,LP Dive 自然會產生指數級的利潤。規模較小的存款人可以通過這種方法獲得更多利潤,並且更容易在較便宜的鏈上進行測試。
人們更容易將AMM 和LP 視為原生對沖工具,而不是存款以賺取收益的工具。該工具所提供的收益過程是,自然地做空一種資產與另一種資產,一直到較低的估值,收益減少,並自動進行多空對沖策略。使用基於delta 的對沖策略的基金或投資者可以將價格變化視為delta,將LP 的價格/數量變化視為gamma。
對於除跳水者之外的所有其他參與者,此動作的負面影響通常都很高。從更廣泛的市場環境來看,持續執行此操作會導致價格壓縮或臨時價格等價,以及分配給跳水者更多代幣,作為承擔他們跳水的任何資產風險的補償。也就是說,在所有資產池中的所有資產中,所有的現貨價格都向最低的平衡值移動。在此期間,跳水者可以使用LP 作為本地對沖工具來利用槓桿,這使得池中的TVL 粘性降低,或者更容易出現“吸血鬼”(MEV 提取)。
對於沒有跳水的投資者來說,通常情況下,資金池APR 產生的協議代幣的費用數額是有利可圖的,儘管不是最大的利潤,因為它承擔的風險比跳水小。如果使用LP 跳水方法增加,儲戶通過深度流動性來鞏固資金,賺取費用的做法將變得更有利可圖。
耦合風險與兩者之間的價格行為相關,這意味著資產的波動性在它與AMM 配對的那一刻就降低了。持續使用跳水策略,特別是槓桿式C 型或T 型跳水,進一步降低了波動性,這導致槓桿式跳水策略的有效性降低。
結論
Yield farm 無利可圖的假設是正確的——跳水者承擔多頭/空頭風險,在短期內比儲戶賺更多的錢。當前使用基於CPMM 的不變量的LP 存在跳水者利用這些軟漏洞的風險,這是不變量使用的機制的副產品。另一方面,這為AMM 和LP 開闢了新的實施和研究領域,尤其是與自動化DEX 相關的領域。通過收集關於這些概念的知識,可以在這些協議中深化鏈上流動性,並且可以圍繞流動性池開發更強大的功能。