StarkNet零知識遞歸證明—STARK已上線,遞歸在成本和延遲方面的優勢異常顯著,還會催生L3 和應用遞歸等新機會。
原文:《Recursive STARKs》 byStarkWare 核心工程師Gidi Kaempfer
翻譯:「StarkNet 中文」社區
作者:技術最前沿
概要
遞歸證明上線主網,用一個證明來擴展StarkEx 應用程序和StarkNet
遞歸證明提升擴展性,降低成本和延遲(鮮有的擴展性和延遲同步發展,而沒有取捨)
遞歸證明為L3 和其他妙用創造了條件
來看看遞歸證明的博文吧,超酷的
倍數擴展!
由Cairo 通用計算提供支持的遞歸證明現已投入生產。這標誌著STARK 對L2 擴展能力的重大提升。單一證明寫入以太坊的交易數量可快速成倍增加。
迄今為止,STARK 證明通過將數万甚至數十萬個交易「匯總」成單一證明寫入以太坊來實現擴展。通過遞歸,許多這樣的證明可以「匯總」成一個單一證明。
這種方法現已應用於眾多基於Cairo 的應用程序:在StarkWare 的SaaS 擴展引擎StarkEx 和無需許可的Rollup StarkNet 上運行的應用程序。
迄今發展歷程
自2020 年3 月主網上線首個證明產生以來,STARK 證明至今經歷了不同發展階段。
STARK 擴展
2020 年6 月,第一個STARK 擴展解決方案StarkEx在以太坊主網部署。 StarkEx 有一個證明器可以在鏈下執行大型計算,生成一個STARK 證明表示交易準確性,還有一個驗證器在鏈上驗證證明的準確性。第一次部署由StarkWare 工程師從零開始親自操刀,因此StarkEx 的功能極大受限。最終我們決定,需要一種支持證明通用計算的編程語言。這樣,Cairo 便應運而生。
Cairo 編程語言
2020 年夏天,Cairo首次亮相以太坊主網。 Cairo 即CPU 代數中間代碼(CPU Algebraic Intermediate Representation [AIR]),內含一個用於驗證相應「CPU」指令集的單一AIR。 Cairo 為更複雜的業務邏輯、任意可計算命題(computational statements)打開了編碼證明的大門,而且更快、更安全。一個Cairo 程序可以證明相應應用程序的執行邏輯。但一個Cairo 程序也可以集合多個此類應用程序,這就是SHARP。
SHARP
SHARP 即共享證明器(SHARed ProSver),可以聚合幾個獨立應用程序的交易,並在一個單一的STARK 證明中證明。應用程序可以組合不同批量交易,更快填滿STARK 證明的容量。交易處理速度和延遲都有所提高。遞歸證明是下一代前沿技術,不僅適用於一些硬編碼邏輯,而且適用於通用計算。
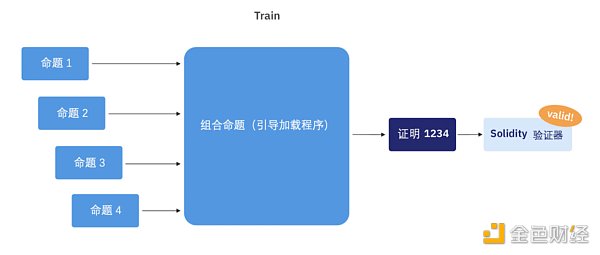
要了解遞歸證明的全部優勢,有必要進一步了解SHARP 迄今為止是如何執行(非遞歸)證明的。圖1 描繪了一個典型的非遞歸流程:
圖1:典型非遞歸證明流程
在這個流程中,命題逐漸到達。容量(或時間)達到一定閾值時,會生成一個大型組合命題(Train)。只有在收到所有單獨命題後,才能證明此組合命題。此證明需要很長時間(大約是單獨證明每個命題所需的時間總和)。
證明極其龐大的命題最終會受到內存等可用計算資源的限制。在遞歸之前,這實際上是限制STARK 證明可擴展性的一大障礙。
什麼是遞歸證明?
通過STARK 證明,證實命題所花費的時間與執行命題所花費的時間大致呈線性關係。此外,如果證明一個命題需要的時間為T,那麼驗證證明所需要的時間大約為log(T) ,這通常被稱為「對數壓縮」。換句話說,使用STARK 讓用戶在驗證命題上的時間要比計算命題的時間少得多。
Cairo允許表達通用計算命題,這些命題可以經STARK 證明所證實,再經相應的STARK 驗證器驗證。
這就是執行遞歸的機會所在:就像可以寫一個Cairo 程序來證明成千上萬的交易正確性,也可以寫一個Cairo 程序來驗證多個
STARK 證明。可以生成一個證明來驗證多個「上游」證明的有效性。這就是我們所說的遞歸證明。
由於對數壓縮和證明時間大致呈線性關係,證實STARK 證明所需的時間相對較短(不久的將來預計只需要幾分鐘)。
在實現遞歸時,SHARP 可以一收到命題就可以對其進行驗證。證明可以各種模式反复地合併成遞歸證明,直到在某個點上,產生的證明提交給鏈上驗證者合約。圖2 就是典型的遞歸證明模式:
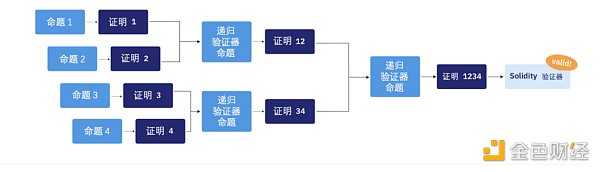
圖2:典型遞歸證明流程
在本例中,有四個命題發送給SHARP(可能源自四個不同應用)。這些命題各自平行證明。然後,每一對證明都由一個遞歸驗證器命題(驗證STARK 證明的Cairo 程序)來驗證,由此產生一個證明。這一命題證實有兩個證明經過驗證。接下來,通過遞歸驗證器命題再次合併這兩個證明。這就產生了一個證明,證實所有四個原始命題。此證明最終可以提交到鏈上,由Solidity 驗證器智能合約進行驗證。
遞歸證明的直接優勢
降低鏈上成本
毫無疑問,我們實現了將多個證明「壓縮」成一個,這意味著每筆交易鏈上驗證成本會大幅更低(其中每個命題可能包含許多交易)。
使用遞歸證明可以消除至今限制證明大小的計算資源障礙(如內存),因為每個命題容量有限,都可以單獨證明。因此當使用遞歸時,遞歸的有效組合命題(Train) 的容量幾乎是無限,每筆交易成本可以降低好幾個數量級。
在實際操作中,降低成本取決於可接受的延遲(以及交易到達的速度)。此外,由於每個證明通常也伴隨相應鏈上數據輸出,因此與單個證明一起寫入鏈上的數據量也會有限。儘管如此,將成本降低一個數量級,甚至繼續提升性能都可以輕鬆實現。
降低延遲
遞歸證明模式可降低證明大型組合命題延遲。有兩個因素起到作用:
1. 接收的命題可以並行證明(而不是證明巨大的組合命題)。
2. 無需等到Train 中的最後一個命題到達即可證明。相反,有新命題加入可以隨時與證明結合。也就是說,加入Train 的最後一個命題的延遲,大致上是證明最後一條命題所需的時間加上證明遞歸驗證器命題(證明所有已經「加入」這個特定Train 的命題)所需的時間。
我們正在積極開發和優化證明遞歸驗證器命題的延遲問題。預計幾個月內證明遞歸驗證器命題會達到幾分鐘的數量級。因此,一個高效的SHARP 延遲可控制在幾分鐘到幾小時,延遲長短取決於對每筆交易鏈上成本的取捨。這是對SHARP 延遲的重大改進。
促進L3 應用
用Cairo 開發的遞歸驗證器命題也開啟了向StarkNet 提交證明的可能性,因為該命題可以寫入StarkNet 智能合約。這允許在StarkNet L2 公共網絡上部署L3。
遞歸模式也適用於來自L3 的聚合證明,由L2 上的單個證明驗證。因此,L3 也可以實現超大規模擴展。
更多妙用
應用遞歸
遞歸為希望進一步擴展其成本和性能的平台和應用程序開闢了更多機會。
每個STARK 證明證實應用於某些「公開輸入」(或Cairo 術語中的「程序輸出」)的命題有效性。從概念上來說,STARK 遞歸將具有兩個輸入的兩個證明壓縮為一個具有兩個輸入的證明。換句話說,雖然證明的數量減少,但輸入數量未變。然後,輸入通常由應用程序用以更新L1 上的某些狀態(例如,更新狀態根或執行鏈上取款)。
如果遞歸命題可以在應用層感知,即識別應用程序本身的語義,那麼遞歸命題既可以將兩個證明壓縮為一個,也可以將兩個輸入組合為一個。最終的命題證實基於應用程序語義的輸入組合的有效性,這就是應用遞歸(Applicative Recursion,參見圖3 示例)。
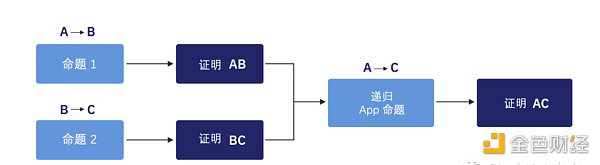
圖3:應用遞歸示例
命題1 證明從A 到B 的狀態更新,而命題2 驗證從B 到C 的進一步更新。命題1 和命題2 的證明可以合併為第三個命題,直接證明從A 到C 的更新。通過應用類似的遞歸邏輯,可以非常顯著地降低狀態更新的成本,達到最終延遲要求。
應用遞歸的另一個重要示例是壓縮來自多個證明的匯總數據。例如,對於像StarkNet 這樣的有效性證明Rollup,L2 每次存儲更新也作為傳輸數據在L1 更新,確保數據可用性。但是,不需要為同一個存儲單元發送多次更新,因為只有經過證明驗證過的交易最終才能滿足數據可用性。此優化已在單個StarkNet 區塊中執行。但是,通過為每個區塊生成證明,應用遞歸可以壓縮多個L2 區塊匯總數據。這可以顯著降低成本,降低L2 出塊時間,而不會犧牲L1 更新的可擴展性。
值得注意的是:應用遞歸可以與前面描述的應用通用遞歸結合使用。但這兩種優化互無關聯。
降低鏈上驗證器的複雜性
STARK 驗證器的複雜性取決於用以驗證的命題類型。特別是對於Cairo 命題,驗證器的複雜性取決於Cairo 語言中允許的特定要素,更具體地說,是支持的內置項(如果把Cairo 比喻成CPU,那麼內置項相當於CPU 中的微電路:計算執行太過頻繁,所以需要優化自身計算)。
Cairo 語言不斷發展並提供越來越多有用的內置項。另一方面,遞歸驗證器只需要使用一小部分內置項。因此,遞歸SHARP 可以通過支持遞歸驗證器中的完整語言來成功支持Cairo 中的任何命題。具體來說,L1 上的Solidity 驗證器只需要驗證遞歸證明,因此驗證器可以僅限於驗證Cairo 語言一個更穩定的子集:L1 驗證器不需要隨最新、最穩定的內置項更新。換句話說,命題不斷演化,複雜的驗證就交由L2 處理,L1 驗證器只需要驗證簡單、穩定的命題。
減少計算足跡
在遞歸之前,聚合多個命題為一個證明受到可用計算實例上可以證明的命題大小(以及生成此類證明所需的時間)的限制。
有了遞歸,無需再證明如此龐大的命題。因為有了更多又小又便宜的計算實例可供使用(儘管計算實例可能要比使用大型單片證明器時需要的更多)。這使得在更多的物理和虛擬環境中部署證明器實例成為可能。
總結
通用計算的遞歸證明現已為包括StarkNet 在內以太坊主網上的多個產品系統服務。
由於可以不斷改進,遞歸的優勢會逐步顯現。並行計算的潛力得以發揮後,Gas 費降低,延遲改善,超高擴展性終將實現。
遞歸在成本和延遲方面的優勢異常顯著,還會催生L3 和應用遞歸等新機會。遞歸驗證器持續優化,性能和成本效益也都會逐漸提升。
附錄
原文:Recursive STARKs
https://medium.com/starkware/recursive-starks-78f8dd401025
原文:Youtube:StarkEx – How Does it Work?
原文:Hello, Cario!
https://medium.com/starkware/hello-cairo-3cb43b13b209
原文:Hello, Cario!
原文:Wikipedia Entry: Recursion
https://en.wikipedia.org/wiki/Recursion
原文:《分形式擴容:從L2到L3》
https://mirror.xyz/starknet-zh.eth/-5oiKxwShIOzGUwuQJzIl070wopcPjqBcypVjRvyC1E