撰文: Iraklis Leontiadis
編譯:Hahaho
可能你正在閱讀本文的時,所使用的瀏覽器和內容終端之間的通信保密也正在運行中,這一過程得益於核心密碼原語實現的身份驗證。可能你沒聽說過類似加密(encryption)、簽名(signatures)、消息認證代碼(message authentication code)等抽象名詞,但端到端的安全也正被這些技術保護著,外部某一方是無法在不被發現的情況下閱讀傳輸的內容亦或改變內容的。在本文中,我們將重點分析數字簽名的內部結構以及它們在數字資產和加密貨幣中的作用。
傳統簽名
銀行支票本質是從發送方到接收方的資金轉移指令,而這一指令由發行支票的銀行確認。出票人要在支票上指定收款人及金額,隨後需要出票人在支票紙上的親筆簽名來驗證。在理想狀態下,不會出現任何問題,指定接收者去銀行,銀行驗證後進行資金轉移。但事實是,每張支票紙上的簽名不是唯一的,經常是相同的,這就使支票簽名容易被偽造。設想一下,如果你的支票被人篡改,轉賬金額多了位0 的損失將是巨大的。
銀行支票
數字簽名
這個問題如何解決呢?在傳統簽名中,發送人簽發信息的手寫簽名是唯一的(或同一的),數字簽名採取的方式是將需要簽名的信息與簽名本身綁定,每一個簽發信息的電子簽名都是一個新的字節流。在這一基礎上想偽造電子簽名,需要解決的難題以目前已有的工具和知識幾乎是不可能的,所以它相對更安全。
發送者可以指定其簽名鑰匙公開和保密的部分,接收者將發送者的公共信息與它的公共密鑰(通常是證書的形式)結合起來,驗證簽名的正確性。
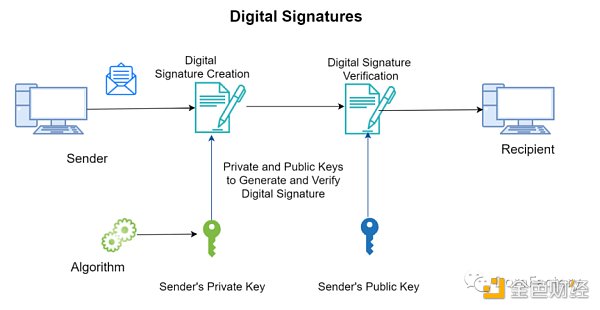
電子簽名
驗證機構將發送者的公鑰及其元數據簽名(可公開識別)進行綁定。協議的安全性不僅依賴於簽名的安全保證、整個過程的安全實現、秘鑰的安全存儲和可靠的通信渠道,還依賴於驗證機構本身是否足夠安全。攻擊者可以執行中間人攻擊或冒充相關方,攻擊驗證機構和發行「虛假」證書的後果是糟糕的,相關例子屢見不鮮,比如Diginotar、Comodo 和MonPass。
數字資產中的簽名
隨著分佈式賬本技術和在此基礎上的金融應用(加密貨幣)出現,人們提起了對數字簽名的興趣。數字簽名是數字資產系統的核心,保證了數字資產所有權,並防止了雙花問題(花費的比持有的多)。
在一個加密貨幣系統中,當史蒂夫想發送特定數量的數字資產(例如比特幣)給勞拉時,史蒂夫會在自己的賬戶簽署一個包含支出信息的字節流,然後,擁有公開信息的礦工(驗證者)驗證簽名的有效性,並根據基本的共識機制,將其作為主分佈式賬本上的一個區塊,最終完成交易。
數字簽名如果出現缺陷,會對系統的公平性和安全性產生破壞性的影響。攻擊者可以通過不安全的私鑰存儲,或底層算法的潛在缺陷,啟動未經授權的交易,造成的損失可能永遠無法恢復。在傳統金融系統中,卡號和密碼就是秘鑰,所以金融數字資產的安全就包括秘鑰的安全和數字簽名的安全。
目前有三種簽名管理分佈式賬本系統:ECDSA、Schnorr 和EdDSA。這些簽名方案都依賴於橢圓曲線組和數學難題。不同的曲線提供不同的效率和安全保證,例如愛德華曲線通常被認為更安全,因為它更容易在恆定的時間內實現,以避免因其通用形式而產生的側信道攻擊。
在下文,我們將把底層的橢圓曲線運算組作為一個「黑匣子」,只強調上面的代數方程。下文的所有簽名,都在一個質數階為q 的基礎組G 進行算術運算,所有的運算都是q 的模運算且存在一個散列函數H,輸入任意字節流,輸出的是Zq 中的元素。
ECDSA 簽名
比特幣網絡上線時,中本聰決定將ECDSA 定為基礎簽名方案。簽名算法的第一步,是對新的隨機k 進行採樣,如果不這樣,對手可以通過不同信息的兩個不同的簽名提取密鑰(例如PS3 被黑事件)。如果重複隨機性聽起來比較極端,那麼只要重複k 中的一部分字節,就足夠以良好的概率提取剩餘的隨機性。
簽名的另一個缺點是,它不易與區塊鏈所需的簽名副產品兼容,即:多重簽名、聚合簽名和MPC 協議。原因是逆元素k^-1 對計算簽名的s 部分的非線性方程的影響。
最後重要的是,ECDSA 根據定義是可塑的(可延展的):兩個不同的簽名可以映射同一個信息。這是可行的,因為(r,s) 和(r,-s modq) 可以通過對s 的形式實施限制來緩解(始終考慮較小的s),驗證信息m。

ECDSA 簽名
Schnorr 簽名
Schnorr 簽名方案,克服了ECDSA 的一些缺點,它具有線性形式,可以更輕鬆地實現其MPC 版本,使聚合和多重簽名的工作量變得更少。與ECDSA 相比,它不具有可塑性,但有更強的理論安全證明分析。然而,對新的隨機性的需求仍然存在,這使它容易受到實施錯誤的影響。

Schnorr 簽名
EdDSA 簽名
EdDSA 消除了對每個消息的新隨機性的需要。如下所述,簽名算法從密鑰和消息中確定地獲取隨機性。此外,EdDSA 是在Edward 曲線上實現的,如Curve25519 和Curve448,這使得它們在實施正確的情況下很容易保持恆定,並提供更有效的代數實現。

EdDSA 簽名
結論
密碼學研究隨著區塊鏈生態系統的設計、實施和部署而發展:閾值密碼學、零知識證明、聚合簽名、VDF、VRF、分佈式隨機信標等。在過去的幾年裡,從研究和工程方面投入到數字簽名的工作量呈指數級增長,我們見證了從協議描述到POC 到實現生產的最短時間週期。
我們也將看到替代上述簽名的新簽名;更快、更安全、更易於實施。從協議描述到POC 再到生產的每一步都需要進行徹底的審查,一個小缺陷都會造成巨大的損失。早期採用到成為標準需要數年時間的積累,加密協議是每個數字金融系統的核心,確保數字資產的安全,一個最佳選擇總是需要權衡取捨。
加密協議在生產環境中不是獨立存在的,安全分析僅是第一步,產品所有者、工程師、QA 和devops 需要與密碼學家加強合作,了解部署加密代碼的風險,並確保免受惡意用戶的影響。完美安全永遠不會存在,在Parfin 我們採取了所有必要的步驟來保護相關基礎設施,盡可能地信任並儘量減少潛在的關鍵信息暴露。