Vitalik：多項式承諾如何讓zk-SNARK 的實現更加高效？

原文標題：An approximate introduction to how zk-SNARKs are possible

原文作者：Vitalik Buterin

原文來源：vitalik.ca

編者註：說到過去十年來誕生的最強密碼學技術，肯定免不了提及零知識證明(zero knowledge proof)。在區塊鏈領域中，它們有兩大應用場景：可擴展性和隱私。 zk-SNARK 作為其中一種zkp 技術，在近幾年來也得到了較大的突破，以太坊上出現了諸如zkSync、Scroll、Hermez 等此類使用zk-SNARK 證明的通用擴容解決方案。

然而，實現zk-SNARK 並不簡單，因為對某個聲明生成了zk-SNARK 證明之後，驗證者需要以某種方式檢查計算中的數百萬個步驟。多項式承諾就是在這裡發揮其作用，即可以將計算編碼為多項式，然後使用一種特殊類型的多項式“哈希”(多項式承諾)，以允許驗證者在極短的時間內驗證多項式等式，即便這些計算背後的多項式規模無比大。

在本文中，Vitalik 介紹了zk-SNARK 技術的工作原理和難點，然後解釋了多項式以及多項式承諾如何讓zk-SNARK 的實現更加高效。

特別感謝Dankrad Feist、Karl Floersch 以及Hsiao-wei Wan 的反饋和校對。

過去十年來誕生的最強密碼學技術大概要數通用簡潔零知識證明，通常稱為zk-SNARK（zero knowledge succinct arguments of knowledge）。 zk-SNARK 允許你生成一個證明(這個證明是針對一些運算得出的特定輸出，可用於對該運算的驗證)，通過這種方式，即使底層計算十分耗時，該證明也可以被快速驗證。 “ZK”（零知識）為證明新增了一個額外特性：證明可以隱藏計算的某些輸入。

例如，您可以對以下聲明生成一個證明：“我知道一個秘密值，如果你將數字添加到挑選的單詞cow 的末尾，然後對其進行1 億次SHA256 哈希運算，那麼輸出的哈希值以0x57d00485aa 開頭”。驗證者驗證該證明的耗時可遠小於自行進行1 億次哈希運算的耗時，而且證明也不會洩漏秘密值。

在區塊鏈領域中，該技術有兩大應用場景：

1. 可擴展性：如果一個區塊的驗證十分耗時，某個人可以驗證區塊並生成一個證明，而其他人只需快速地驗證證明即可

2. 隱私：你可以證明你有權轉移某些資產（你收到了該資產，而且你還沒有轉走），而不透露該資產的來源。這不會對外洩漏交易雙方的信息，確保了交易的安全性。

然而，zk-SNARK 是相當複雜的；實際上，就在2014-17 年，它們還常被稱為“月亮數學”。好消息是，從那時起，協議愈發簡化，我們對它們的理解也愈發深入。本篇博客將試圖以一種數學水平普通的人能理解的方式來解釋ZK-SNARKs 的工作原理。

注意，我們將聚焦於可擴展性；一旦有了可擴展性，這些協議的隱私性就相對容易實現，因此我們將在最後回歸這個主題。

為什麼ZK-SNARK “會”很難

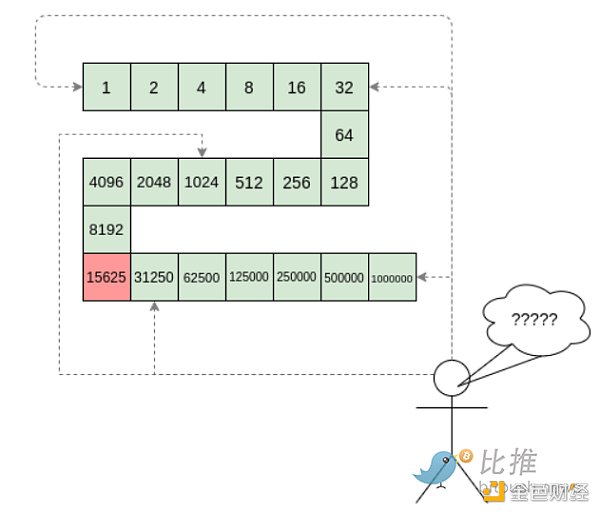
以開頭例子為例：我們有一個數字（我們可以將末尾跟著秘密輸入的“cow” 整體編碼為一個整數），我們計算該數字的SHA256 哈希，然後重複做9999999 次，最後我們檢查輸出的開頭。這裡面的計算量特別大。

一個“簡潔（succinct）”證明指的是證明大小和驗證耗時的增長遠慢於需驗證計算量的增長。如果我們想要一個“簡潔”證明，我們就不能要求驗證者在每輪哈希中做一些運算（因為那樣的話，驗證耗時將與計算量成正比）。相反，驗證者必須以某種方式檢查整個運算過程，而不必窺視運算過程中的每個部分。

有一種自然的技術就是隨機抽樣：讓驗證者只在500 個不同的地方檢查運算的正確性，如果所有的500 個檢查都通過了，那麼認為運算過程的其餘部分也大概率沒問題？

該流程甚至可以通過使用Fiat-Shamir 啟發式（Fiat-Shamir heuristic）轉化為非交互式證明：證明者計算運算過程的默克爾根，基於默克爾根偽隨機地選取500 個索引，並提供對應的500 個默克爾分支。核心思想是證明者並不知道將要揭示哪些分支，直到他們已經對數據生成了“承諾”。如果惡意證明者在了解到需要檢查哪些索引後試圖篡改數據，那麼這會改變默克爾根的值，而這將導致一組新隨機索引被選出，這將需要再次去篡改數據…讓惡意證明者陷入無休止的循環中，無法達成目的。

但不幸的是，簡單地隨機抽查運算過程存在一個致命的缺陷：運算過程本身並不健壯。如果惡意證明者在計算過程中的某個位置翻轉一個比特，可以導致一個完全不同的結果，而隨機抽樣驗證者幾乎永遠不會發現。

只需一次故意的插入錯誤，就會導致計算得出完全錯誤的結果，而這幾乎不會被隨機檢查所捕獲。

如果要提出一個zk-SNARK 協議，那麼很多人會走到上面這步，然後陷入困境，最終放棄。不單獨查看每個計算片段的情況下，驗證者究竟如何才能夠校驗每個計算片段？事實證明，有一個絕妙的解決方案。

多項式

多項式是一類特殊的代數表達式，具有以下形式：

• x+5

• x4

• x3

• +3×2

• +3x+1

• 628×271

• +318×270

• +530×269

• +…+69x+381

也就是說，它們是有限個形式為cxk 的項之和。

多項式有許多有趣的特性。但這裡，我們將聚焦於多項式的一個特性：多項式是一個可以包含無限信息量（多項式顯然可視為一個整數列表）的單一數學對像上。面的第四個示例包含tau 的816 位的信息，而且我們能夠很容易地想像出一個包含更多信息量的多項式。

此外，多項式間的單個等式就能夠表示無限個數間的方程。例如，考慮等式A(x)+B(x)=C(x)。如果該等式是正確的，那麼下面也是正確的：

• A(0)+B(0)=C(0)

• A(1)+B(1)=C(1)

• A(2)+B(2)=C(2)

• A(3)+B(3)=C(3)

可以類推到每個可能的下標。甚至，你可以構造特地表示一組數字的多項式，這樣你就可以一次性地檢查眾多等式。例如，假設您想檢查：

• 12 + 1 = 13

• 10 + 8 = 18

• 15 + 8 = 23

• 15 + 13 = 28

您可以使用一個名為拉格朗日插值的方法來構造多項式：A(x) 在某些特定下標集合（例如(0，1，2，3) 上的輸出為(12，10，15，15)），B(x) 在相同下標上的輸出為(1，8，8，13)，如此類推。準確地說，以下是相應的多項式：

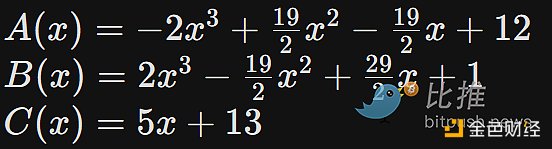
用這些多項式校驗等式A(x)+B(x)=C(x) 相當於同時校驗上述四個等式。

將多項式與自身進行比較

甚至，你可以用一個簡單的多項式等式來校驗相同多項式的大量相鄰取值的關係。這稍微更進一步。假設您想校驗，對於給定的多項式F，在整數範圍{0,1…98} 內滿足F(x+2)=F(x)+F(x+1)（因此，如果您還校驗F(0)=F(1)=1，那麼F(100) 將是第100 個斐波拉契數）。

作為多項式，F(x+2)−F(x+1)−F(x) 不會正好為零，因為它在x={0,1…98} 範圍外的取值是不受限的。但我們可以做一些巧妙的處理。一般而言，有這樣一條定則：如果多項式P 在某些集合S={x1，x2…xn} 上的取值為零，那麼可以表示為P(x)=Z(x)∗H(x) 的形式，其中Z(x)=(x−x1)∗（x−x2)∗…∗(x−xn)，而且H(x) 也是一個多項式。換句話說，在某個集合上值為零的任一多項式可以表示為在相同集合上值為零的最簡（最低階）多項式的（多項式）倍數。

為什麼會這樣？這其實是多項式長除法的一個巧妙的推論：因式定理（the factor theorem）。我們知道，當用Z(x) 除P(x) 時，我們將得到商Q(x) 和余數R(x)，滿足P(x)=Z(x)∗Q(x)+R(x)，其中餘數R(x) 的階嚴格小於Z(x)。因為我們知道多項式P 在集合S 上的取值為零，這意味著多項式R 在集合S 上的取值也必須為零。因此，我們可以通過多項式插值簡單地計算R(x)，因為它是一個階至多為n−1 的多項式，而我們知道其中的n 個取值（集合S 上的取值為零）。使用上述所有零值進行插值得到零多項式，因此，R(x)=0，H(x)=Q(x)。 （譯者註，一個有n 個解的n−1 次多項式必為零多項式）

回到我們的例子上，如果我們有一個編碼了斐波那契數的多項式F（因此，在x={0,1…98} 上滿足F(x+2)=F(x)+F(x+1)，那麼我可以通過證明多項式P(x)= F(x+2)−F(x+1)−F(x) 在該範圍的取值為零來向你證明F 確實滿足該條件： H(x)=(F(x+2)−F(x+1)−F(x))/Z(x)，其中Z(x)=(x−0)∗(x−1)∗…∗(x−98).

你可以自行計算Z(x)（理想情況下會被提前計算出來），檢查該等式，如果檢查通過，那麼F(x) 的確滿足條件！

現在，退一步，留意一下我們做了什麼。我們將一個步長100 的計算（計算第100 個斐波那契數）轉換為單個多項式等式。當然，證明第N 個斐波那契數的取值意義不大，尤其是因為斐波那契數具有閉合形式。但你可以使用完全相同的底層技術，只需一些額外的多項式和更複雜的等式，就可以對任意步長的任意計算進行編碼。

現在，如果存在一種使用多項式校驗等式的方法，而且這種方法比檢查每個係數快得多…

多項式承諾

再一次，事實證明，這樣的方法是存在的：多項式承諾。最好把多項式承諾看作一種對多項式進行“哈希”的特殊方法，該哈希擁有額外特性，即你可以通過校驗多項式哈希間的等式來校驗多項式間的等式。不同多項式承諾方案在適用等式類型上有著不同的特點。

下面是一些常見的例子，您可以使用各種多項式承諾方案（我們使用com(P)來表示“對多項式P 的承諾”）：

• 相加：給定com(P)、com(Q) 和com(R)，檢查是否滿足P+Q=R

• 相乘：給定com(P)、com(Q) 和com(R)，檢查是否滿足P∗Q=R

• 在某個點上求值：給定com(P)、w、z 和一個補充證明（或“見證”）Q，驗證P(w)=z

值得注意的是，這些原語可以相互組合。如果支持加法和乘法，那麼你可以這樣計算：為了證明P(w)=z，你可以構造出Q(x)=

（P(x)−z）/（x−w）， 然後驗證者可以驗證:

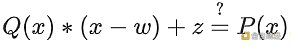
這行得通是因為如果存在這樣一個多項式Q(x)，那麼P(x)−z=Q(x)∗(x−w)，這意味著P(x)−z 在w 處等於零（因為x−w 在w 處等於零），因此P(x) 在w 處等於z。

如果你能計算出某點的取值，那麼你可以進行各種校驗。這是因為有一個數字定理表明：大體上，如果一些包含了一些多項式的等式在一個隨機選擇的下標下成立，那麼對多項式整體而言等式基本為真。因此，如果我們只有一個證明某點取值的機制，那麼我們就可以通過一個交互式遊戲進行驗證，如我們的方程P(x+2)−P(x+1)−P(x)=Z(x)∗H(x)：

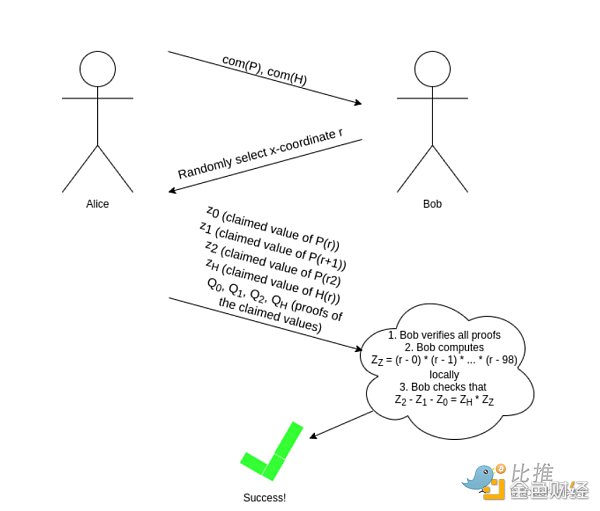
正如前面提到的，我們可以使用Fiat-Shamir 啟發式使其轉化為非交互式：證明者可以令r=hash(com(P), com(H))（其中hash 是任一加密哈希函數；它不需要擁有任何特殊屬性）併計算r。證明者不能通過挑選只“符合”特定r 的P 和H 來進行“欺詐行為”，因為他們在選取P 和H 時不知道r！

快速回顧

• ZK-SNARK很難，因為驗證者需要以某種方式檢查計算中的數百萬個步驟，而無需直接地檢查每個單獨的步驟（因為這會十分耗時）。

• 我們通過將計算編碼為多項式來解決這個問題。

• 單個多項式可以包含無限大的信息量，而且單個多項式表達式（例如，P(x+2)−P(x+1)−P(x)=Z(x)∗H(x)）可以代表無限個數間的方程。

• 如果你可以驗證多項式等式，那麼你同時在隱式地驗證所有的數值等式（用任何實際x 下標替換多項式中的x）。

• 我們使用一種特殊類型的多項式“哈希”，稱為多項式承諾，以允許我們在極短時間內驗證多項式等式，即使背後的多項式規模非常大。

那麼，這些神奇的多項式哈希是如何工作的？

目前有三種被廣泛使用的主流方案：bulletproofs, Kate and FRI。

• 這裡是Dankrad Feist對Kate承諾的描述：https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html

• 這裡是curve25519-dalek團隊對bulletproofs的描述：https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/index.html，而這裡是我的圖解：https://twitter.com/VitalikButerin/status/1371844878968176647

• 這裡是對FRI的描述，我寫的…：https://vitalik.ca/general/2017/11/22/starks_part_2.html

哇，哇，別緊張。試著簡單地講解其中一個，不要把我帶到更可怕的鏈接上

老實說，它們沒有那麼簡單。這就是為什麼所有的這些數學理論直到2015 年左右才真正崛起的緣故。

請？

在我看來，FRI 是最容易理解透的（如果你願意把橢圓曲線配對elliptic curve pairings 看作黑盒，Kate 會更容易理解，但配對確實很複雜，所以總體來說我覺得FRI 更簡單）。

以下是FRI 工作原理的簡化版（簡單起見，免去真正協議中的許多技巧和優化）。假設你有一個階小於n的多項式P。對P 的承諾是某組預選下標取值的默克爾根（例如，{0,1…8n−1} ，儘管這並不是最高效的選取方式）。現在我們需要額外添加一些東西來證明這組取值來自一個階小於n 的多項式。 （譯者註，需要驗證多項式階小於n 的原因是保證作惡者通過隨機抽樣概率盡可能低，給定多項式P，一個基本擬合P 的另一個多項式Q，也是能通過隨機抽樣的，但Q 的特點是其階要足夠大才能成功）

我們要求證明者提供Q(x) 和R(x) 的Merkle 根。然後，我們生成一個隨機數r，並要求證明者提供一個“隨機線性組合”S(x)=Q(x)+r∗R(x)。

我們偽隨機抽樣了一大組下標（像之前一樣，使用提供的Merkle根作為隨機種子），並要求證明者在這些下標處提供P、Q、R 和S 的Merkle 分支。在每個提供的下標處，我們校驗：

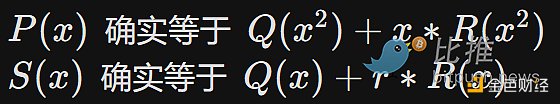
如果我們做了足夠校驗，那麼我們可以確信S(x) 的“預期”值與“提供”值最多（例如，1%）是不同的。

從這裡開始，我們簡單地用S 重複上面的遊戲，逐步“降低”我們關心的多項式的階，直到多項式的階低到我們可以直接校驗的程度。

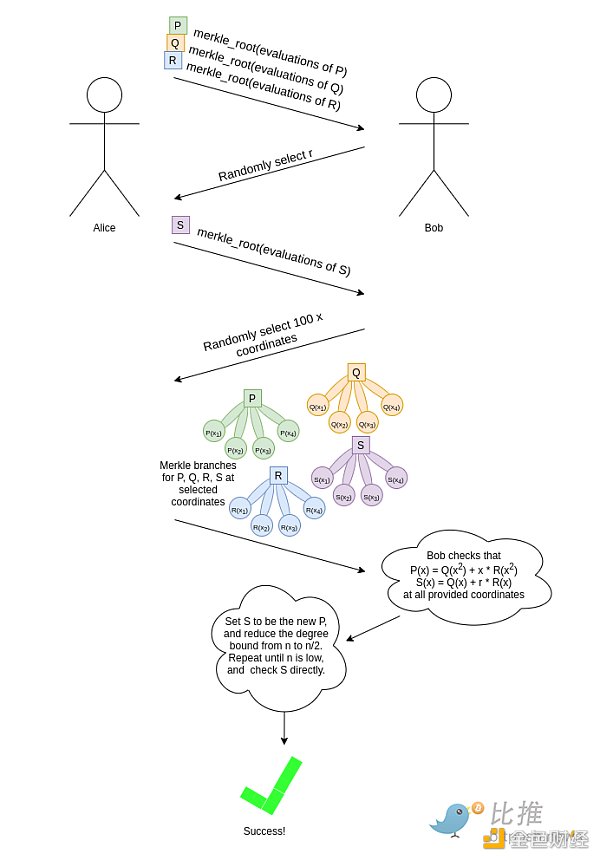
和前面的示例一樣，這裡的“Bob”是一個抽象概念，對密碼學家在思維上論證協議非常有用。事實上，Alice 自己生成了完整證明，為了防止她作弊，我們使用Fiat-Shamir：我們根據此前證明中生成的數據的哈希隨機選取每個樣本的下標或r 值。

（在該簡化協議中）一個對P 完整的“FRI承諾”包括：

流程中的每步都可能會引入一些“誤差”，但如果您進行了足夠多的檢查，那麼總誤差將低到你可以證明P(x) 在至少80% 的下標處等於一個階小於n 的多項式。這足以滿足我們用例的需求：如果你想在zk-SNARK 中作弊，你需要對少數值進行多項式承諾，其多項式的取值會在多處不同於真正階小於n 的多項式，因此任何對其進行FRI 承諾的嘗試都會失敗。

此外，您仔細檢查一下，FRI 承諾中對象的總數和大小是O(log階)，因此，對於大型多項式，承諾實際上比多項式本身小得多。

為了檢查這類不同多項式承諾間的等式（例如，給定對A、B 和C 的FRI 承諾，檢查A(x)+B(x)=C(x)），只需簡單地隨機選擇很多下標，要求驗證者提供在每個多項式的這些下標處的Merkle 分支，並驗證等式在每個下標處成立即可。

上面描述的是一種效率極低的協議；有很多代數技巧可以將協議效率提高約100 倍，如果你想要一個切實可行的協議，比如在區塊鏈交易中使用，你需要使用這些技巧。特別是，例如，Q 和R 實際上不是必要的，因為如果你非常聰明地選擇取值點，你可以直接從P 的取值重構出所需Q 和R 的取值。但是上面的描述應該足以讓你確信多項式承諾從原理上是可行的。

有限域

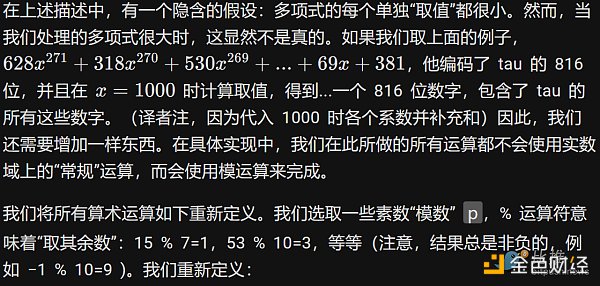
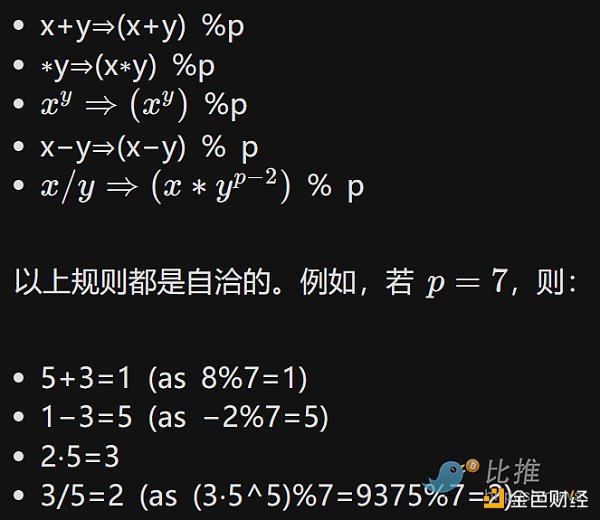
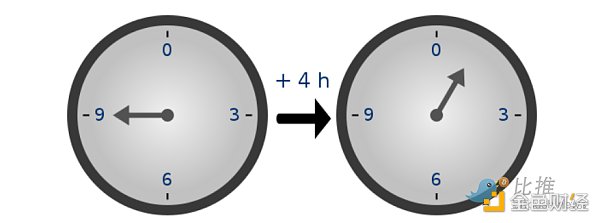
因為數字的“回環”方式，模運算有時被稱為“時鐘數學”

通過模運算，我們創造了一個全新的算術系統，它和傳統算術一樣是自洽的。因此，我們可以討論該域中的所有同類結構，包括我們在“常規數學”中討論的多項式。密碼學家喜歡使用模數學（或者，更一般的，“有限域”），因為任何模運算結果的大小都會有界-無論你做什麼，值都不會“超出”集合{0,1,2…p−1}。即使計算有限域中一個一百萬次多項式，也不會得出一個集合以外的值。

將計算轉化為一組多項式等式更具意義的例子？

隱私

但這裡有一個問題：我們怎麼知道對P(x) 和R(x) 的承諾不會“洩漏”信息（使得能夠揭示我們試圖隱藏的P(64) 的確切值）？

這裡有些好消息：這些證明是對大量的數據和計算生成的小證明。因此，一般來說，證明往往不夠大，只能暴露一點點信息。但我們能從“只有一點點”推進到“零”嗎？幸運的是，我們可以。

在這裡，一個相當通用的技巧是往多項式添加一些“模糊因子”。當我們選定P時，將Z(x) 的小倍數加到多項式中（即，取隨機E(X)，令P′(x)=P(x)+Z(x)∗E(x)）。這並不會影響命題的正確性（事實上，P′ 在“在計算發生”的下標處的值與P 相同，因此它仍是有效的轉義版本），但它可以在承諾中添加足夠多的額外“噪聲”，使得任何餘下信息不可恢復。此外，對於FRI，重要的是不要對計算發生範圍的隨機點進行採樣（在本例中為{0…64} ）。 （譯者註，這樣即使是同樣的多項式也會讓人猜不到）

我們能再回顧一下嗎？ ？

• 最優秀的三類多項式承諾是FRI、Kate 和bulletProof。

• Kate在概念上是最簡單的，但它依賴於非常複雜的橢圓曲線配對“黑盒”。

• FRI很酷，因為它只依賴哈希；它的工作原理是將多項式逐漸歸約為階越來越低的多項式，並在每步進行隨機抽樣檢查，使用Merkle 分支來證明等價性。

• 為了防止單個值大小的膨脹，我們不在整數上做算術運算和多項式運算，而是在有限域上做所有事情（通常是對一些素數p 進行模運算）

• 多項式承諾天然支持隱私保護，因為生成的證明已經比多項式小得多了，因此多項式承諾只能暴露多項式中一點點信息。但我們可以往多項式添加一些隨機性，將暴露的信息從“一點點”減少到“零”。

哪些問題仍在研究當中？

• 優化FRI：已經有很多涉及精心挑選的取值域的優化，“DEEP-FRI”，以及一系列其他讓FRI更高效的技巧。 Starkware 及其他人正在研究這塊。

• 將計算編碼為多項式的更佳方法：找出將涉及哈希函數、內存訪問和其他特徵的複雜計算編碼為多項式等式的最高效方法仍是一個挑戰。在這方面已經取得了很大的進展（例如，見PLOOKUP)，但我們仍需更多的進展，特別是如果我們想將通用虛擬機執行編碼為多項式的話。

• 增量可驗證計算：如果隨著計算繼續能夠高效地“擴展”證明，那就太好了。這在“單證明者”情況下很有價值，而且在“多證明者”的情況下也很有價值，特別對於不同參與者創建區塊的區塊鏈而言。最近一些在這方面的工作，請參見Halo。