Figment Capital：深入解讀零知識證明加速

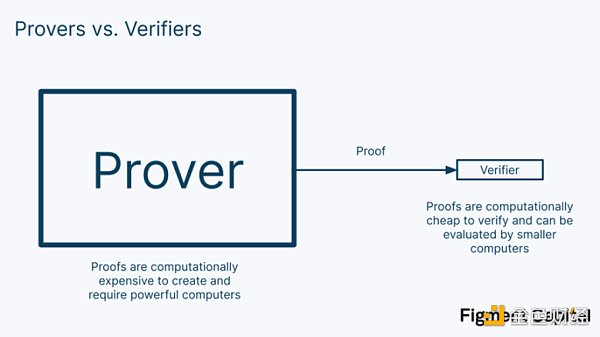
零知識證明允許一個團體在向另一個團體證明一條聲明時不需要透露除去「該聲明為真實的」的信息以外的任何額外信息。儘管這項密碼原語早在上世紀八十年代就已出現，但直到區塊鏈技術的萌發，零知識證明才發現其實際應用，包括區塊鏈擴展、隱私、互操作性，和身份。

儘管聲稱其可以解決區塊鏈技術中的許多最重大的難題，零知識證明仍舊是一項不成熟的技術。在這些問題之中，最主要的其中之一是其證明時間之久。零知識技術應用在不斷改進，其證明的複雜程度也在改進。這些聲明需要更大的算數電路，導致證明時間飆升。生產一個零知識證明可能需要比底層計算增加多達百萬倍。相應地，有大量的團隊正在研究可以改進加速零知識證明所需要的軟件和硬件。

在本文中，我們將提供加速零知識證明的概覽。我們將總結生產零知識證明的主要操作作為討論的起點，並在之後轉向討論這些操作可以如何被加速。

快速上手：什麼是零知識證明？

零知識證明允許一方（通常被稱為證明者），向另一方（通常被稱為驗證者）證明他們成功地完成了一次計算。一個零知識證明擁有以下三個關鍵特性：

• 完整性：如果證明者生成了一項有效的證明，一個誠實的驗證者將視該聲明是有效的。

• 合理性：如果該聲明是虛假的，一個證明者將無法生成一項看起來有效的證明。

• 零知識：如果該聲明是真實的，一個驗證者不會知道除去「該聲明是真實的」以外的任何信息。

區塊鏈背景下最主要的零知識證明的類型是zk-SNARK（全稱是「零知識的簡潔的非交互式知識論證」）。這終證明在上述的傳統的零知識證明的三個特性之上額外有兩條特性：簡潔性和非交互式。具有簡潔性意味著證明的規格小，通常只有幾百字節，並且可以迅速地被驗證者檢驗。非交互式的特性意味著證明者和驗證者之間不需要交互，單單該證明本身已經足夠。較老的零知識證明需要證明者和驗證者之間互發信息以生成一項證明。

簡介性使零知識證明能夠快速地驗證，且從計算角度來看很便宜。這使它們成為了一項很棒的擴展技術。在有效性rollup（也就是零知識rollup）中，強大的證明者能夠計算數以千計的交易的輸出，針對它們的正確性生產一個簡潔的證明，並將它們發送到底層鏈上。在那裡，驗證者能夠檢驗該證明並立刻接受所有已包含的交易的結果，而無需再自行計算。因此，在底層鏈保持去中心化的同時，網絡得以進行擴展。

將上千條交易打包進單一的證明需要巨量的計算工作，從而導致證明時間變長。冗長的證明時間會導致同樣冗長的最終確認時間。因為在交易和證明被發送至底層鏈之前，用戶的交易沒有完全的最終性。而這一過程可能要花一些時間。例如，在Starknet，我們預期證明時間初步上將需要幾個小時。零知識證明在更好的操作、安全、和UX 上都需要加速。

一個零知識證明系統包含三個步驟：配置，證明的生成，以及證明的檢驗。

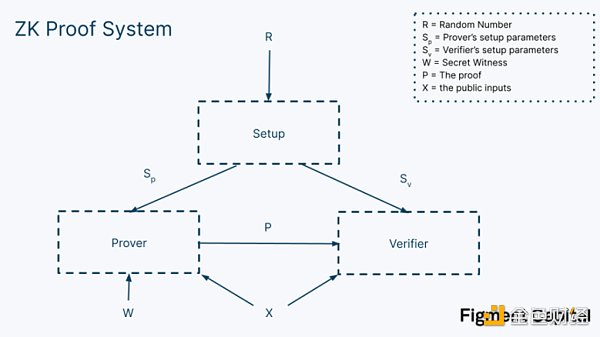
在證明中要用到6 個值：

• R – 隨即數字：建立一個零知識證明系統需要一個一次性的秘密隨機數。如果任何群體知道了該隨機數，他們就可以破解代碼並確認秘密輸入值，消除其零知識屬性。這便是「可信設置」的概念從何而來。在可信配置中，不同群體聚到一起，共同生成該隨機數，以保證沒有任何個體能夠知道該秘密。作為一名用戶，你必須信任該設置是被正確完成的（也就是說，沒有人知道R），以確保你的信息是私密的。注意，STARK 並不要求可信設置。

• Sₚ – 證明者設置常數：設置完成後將交由證明者的常數，允許其驗證一項有效的證明。

• Sᵥ – 驗證者設置常數：設置完成後將交由驗證者的常數，允許其驗證一項有效的證明。

• X – 公開輸入值：我們用於計算的輸入值。這些將被給到證明者和驗證者，且並不是保密的。

• W – 私密輸入值：這是秘密的輸入值，被稱作見證，只會被給到證明者。需要注意的是，在上面的圖表中，見證不會被交給驗證者。零知識的關鍵就是它使我們能夠證明有關見證的聲明，且不需要洩露見證。

• P – 證明：這是由證明者創建、發送給給驗證者的證明。

以上就是深入淺出的「什麼是零知識證明？」。就是這麼簡潔明了！當你真正過一遍其原理的時候，你會發現它其實挺簡單。但是如果要明白如何加速零知識證明，我們就必須先明白它們在幕後是如何工作的。

MSM 與NTT

零知識證明生成有兩大主要瓶頸：多標量乘法（Multi-scalar Multiplication，MSM）和數論變換（Number Theoretic Transform，NTT）。這兩項操作自己就能占到證明生成時間的80% 到95% ，具體則取決於零知識證明的承諾方案和具體的執行。首先，我們會介紹這些操作，其後，我們將提供各個操作能夠如何加速的概覽。

素數有限場

讓我們從素數有限域開始。 MSM 和NTT 都發生在素數有限域中，因此了解素數有限域是重要的第一步。

想像一下，我們有一組0-10 的數字。我們可以給這組數字添加一條規則，即：一旦我們數過數字10 ，我們就從數字0 重新開始。如果我們減去最低的數字0 ，我們就從最後的10 開始。

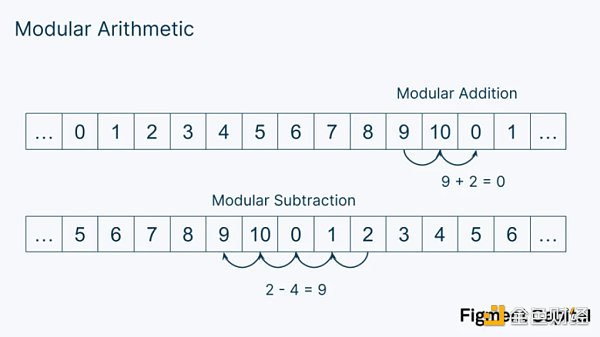
我們稱數字11 為模數，因為它是我們開始「循環」的數字。這種類型的數學被稱為模算數。我們與模算數互動的最直觀的經驗是在報時時，我們以12 為模數計算小時。

乘法也適用於模算數。如果我們把9 ✕ 3 = 27 ，我們會得到5 作為我們的輸出（如果你想檢查，自己算一下！）。這被稱為簡單除法中的「餘數」。我們可以把解決方案寫成：

9 ✕ 3 mod( 11) = 27 mod( 11) = 5, 因為11 ✕ 2 + 5 = 27. 2 代表我們循環的次數。

請注意，在我們這個0-10 的集合中，無論我們選擇什麼數字做加法、減法或乘法，我們的結果永遠是這個集合中的另一個數字。換句話說，沒有辦法跳出這個集合。在模算術中，除法要稍微複雜一些，但它的工作原理是相似的。因為我們的集合具有這種封閉性，所以它是一種特殊類型的集合，稱為場。

從一個場到一個素數有限場是微不足道的。一個有限場是一個具有有限個元素的場。素數有限場是一個以素數為模數的有限場。由於我們的例子中0-10 的集合是有限的，並且以質數11 作為其模數，所以它是一個質數有限場！

多標量乘法

現在我們已經涵蓋了素數有限場，我們能夠理解MSM 了。假設我們有兩行數字。我們可以對這些行進行的一個操作是，將一行中的每個元素，與另一行中的相應元素相乘，然後將乘積相加成為一個單一的數字。這種操作被稱為點積，在數學中常用。下面是它的樣子：

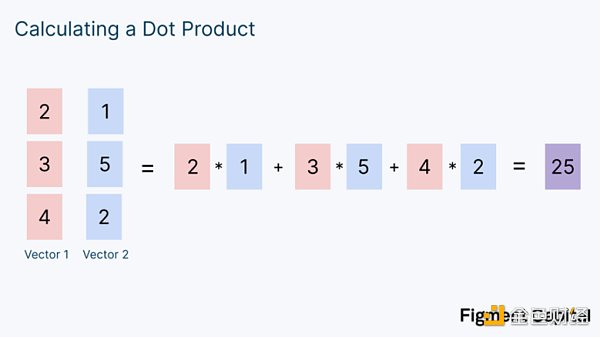
一個向量就是一個數字列表。注意，我們把兩個向量的數字作為輸入，並產生一個單一的數字作為輸出。現在，讓我們修改一下我們的例子。我們可以不計算2 個數字向量的點積，而是計算一個點的向量和一個數字向量的點積。

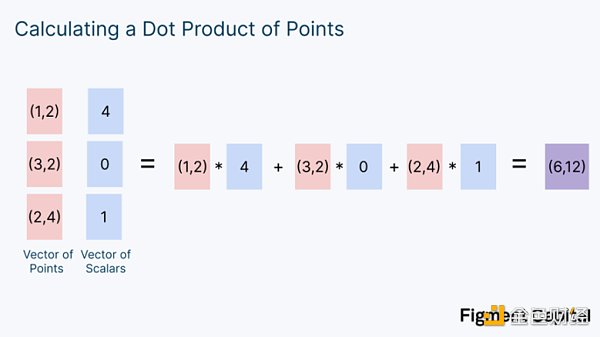
一個標量就是一個普通的數字。在這種情況下，我們的輸出不是一個單獨的數字，而是一個網格上的新點。從圖形上看，上面的計算看起來像下圖這樣：

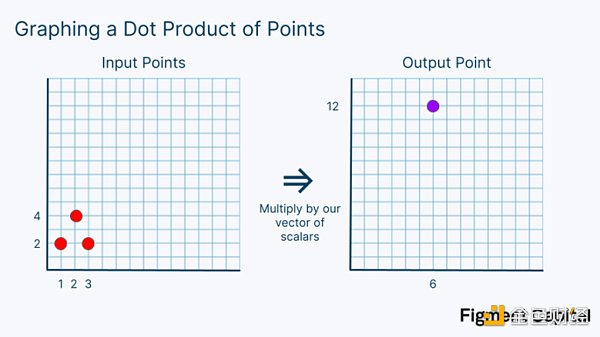
這個計算包括將網格上的每一個點按一定的係數進行縮放，然後將所有的點相加，得到一個新的點。請注意，無論我們在這個網格上選取什麼點，無論我們用什麼標量乘以它們，我們的輸出總是網格上的另一個點。

正如我們可以用網格上的點而不是整數來計算點積一樣，我們也可以用橢圓曲線上的點來進行這種計算。橢圓曲線（EC）看起來像這樣：

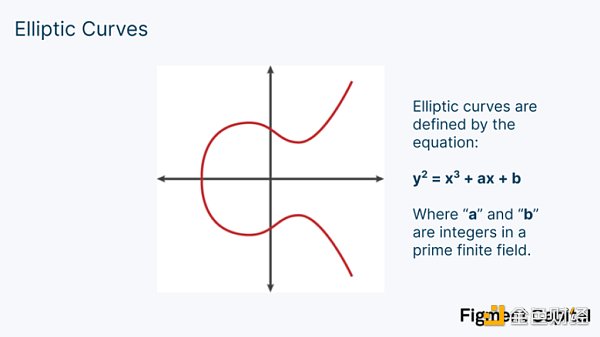
我們在零知識中使用的數學涉及橢圓曲線，它位於素數有限場中。因此，無論我們對橢圓曲線上的任何一點進行何種加法或乘法，其輸出都將是橢圓曲線上的另一個點。標量的點積會輸出另一個標量，（x, y）坐標的點積會產生另一個坐標，而橢圓曲線點的點積會產生另一個EC 點。從視覺上看，橢圓曲線的點積看起來像這樣：

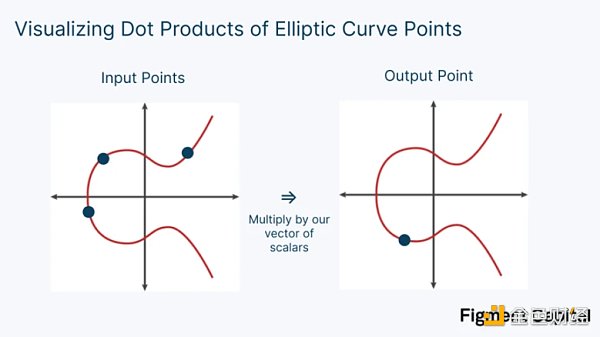
橢圓曲線上的一個點與一個標量相乘稱為點乘法。將兩個點相加稱為點加。點乘法和點加法都會在橢圓曲線上輸出一個新的點。

在視覺上，橢圓曲線加法是一個簡單的操作。給定任何兩個EC 點，我們可以在它們之間畫一條線。如果我們看一下這條線與曲線第三次相交的地方，我們可以找到它在X 軸上的反射，從而找到這兩個點的和。要把一個點G 加到自己身上，我們要找到曲線的切線，看看那條線與曲線的交點，然後在X 軸上畫一條反射線，直到再次與曲線相交。那個點就是2 G. 因此，點乘法也很容易直觀化。它只是涉及到將一個點本身相加。

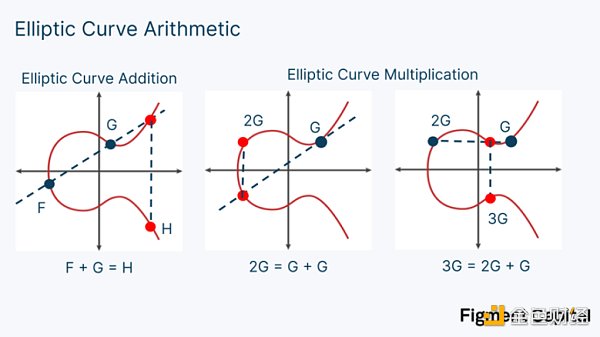
關於如何從數學上計算EC 加法的詳細解釋超出了本文的範圍。在高層次上，EC 加法將兩個非常大的整數相加，並以某個大的素數為模數。

這種將多個橢圓曲線點，與標量相乘（點乘），然後相加（點加），得到橢圓曲線上的一個新點的操作稱為多標量乘法（MSM）。 MSM 是ZKP 生成中最重要的操作之一，然而它只是一個點積。

實際上比這還要簡單： MSM 可以被改寫為一堆EC 點的加法。

因此，每當你聽到「多標量乘法」時，我們所做的就是把許多EC 點加在一起，得到一個新的EC 點。

水桶法

「水桶法」是用於加速MSM 計算的一個巧妙的技巧。點加法計算在計算上是很便宜的。 MSM 的問題在於點乘法。在真正的零知識證明中，我們的EC 點所乘的標量是非常大的。對於每一個點乘法，計算都需要數百萬次的求和。幸運的是，有一個簡單的方法可以加快MSM 的速度：我們可以並行計算所有的點乘法。

水桶法的關鍵思想是，我們可以將這些大點積減少為小點積，並行計算，然後將它們加在一起。

下面是它的工作原理。回顧一下，在計算機中，數字被表示為1 和0 的二進制數字。

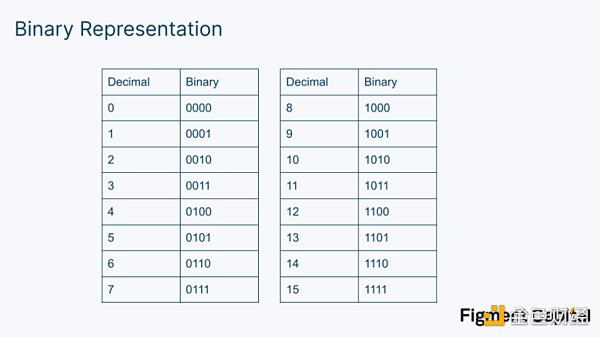
因此，在我們的計算機上，我們的EC 乘法實際上可能看起來像這樣（只是用大得多的二進制數字）：

水桶法的第一步是將這些二進制標量分割成一定位數的窗口。在下面的圖片中，我們將標量分割成4 比特的窗口。

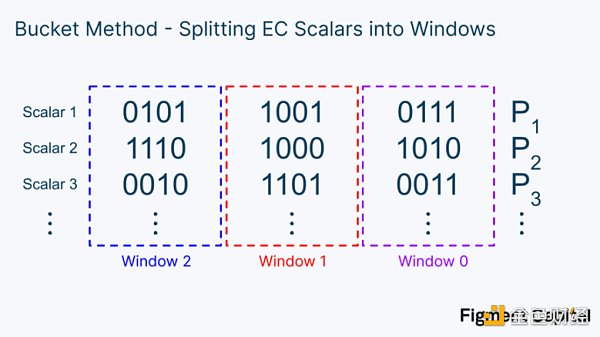
請注意，每個桶涵蓋的數值從0000 = 0 到1111 = 15. 在我們將標量分解成4 位的窗口後，我們可以將每個EC 點分類到涵蓋0-15 範圍的桶中。

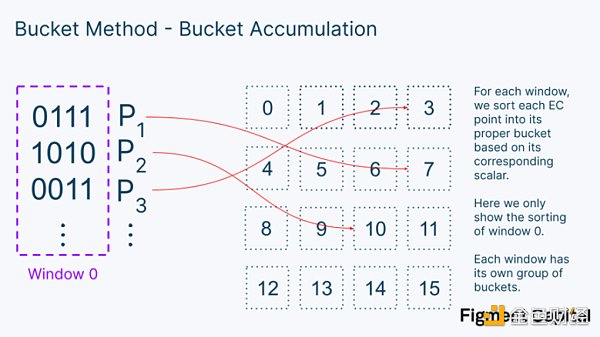
對於一個給定的窗口，一旦我們把每個點都分類到一個桶裡，我們就可以把所有的點加起來，得到每個桶的一個點。

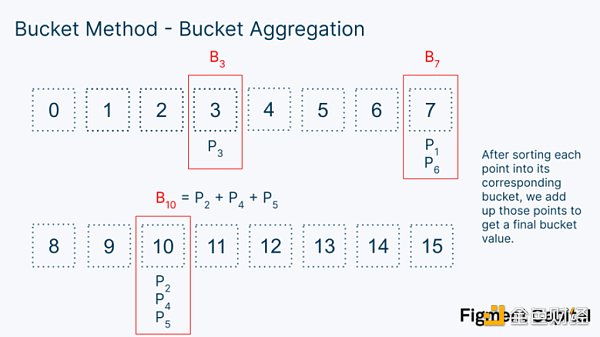
請注意，在這個例子中，我們只顯示了幾個點，但實際上，每個桶都包含很多數字。一旦我們有了每個桶的值，我們就可以把它們都乘以它們的桶號，得到整個窗口的最終值。這個窗口的計算只是另一個點積。

一旦我們計算出每個窗口的窗口值，我們就可以把它們全部加起來，得到我們的最終輸出。但首先，我們需要調整的是，每個窗口代表不同的數值範圍。要做到這一點，我們需要將每個窗口乘以2 ⁱ**ˢ，其中i 是窗口編號，s 是窗口長度。我們的窗口是4 比特長，所以窗口大小是4 。

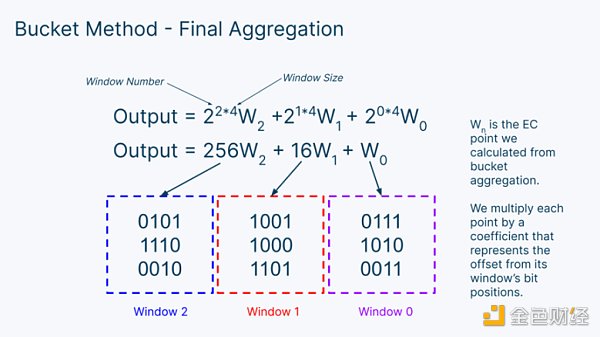
然後，我們只需將所有數字相加，就可以得到我們的MSM 的最終輸出結果！簡而言之，水桶法包括3 個步驟：桶式積累、桶式匯總和窗口匯總。

• 桶式積累：對於每個窗口，根據其係數，將每個EC 點分類到一個桶中。然後將每個桶中的所有點相加，得到每個桶的最終值。

• 桶式匯總：對於每個窗口，用所有的桶值乘以它們的桶號，然後加在一起，得到一個窗口值。

• 窗口匯總：把所有的窗口值，乘以它們的位偏移量，然後把它們加在一起，得到你最終的橢圓曲線點。

幾乎所有的零知識證明加速設置都使用了這種水桶法。例如，下面是由Jump Crypto 和Jump Trading 團隊共同設計的MSM 的硬件加速器的圖示。它的大部分內容看起來很熟悉！

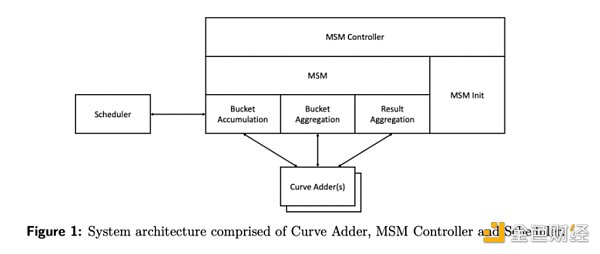
水桶法通過並行計算和有效平衡硬件上的工作負荷來加速MSM，從而使證明生成時間得到顯著改善。

數論變換（NTT）

NTT，也被稱為快速傅里葉變換（FFT），是零知識證明生成中的第二個關鍵瓶頸。其操作和基礎數學比MSM 更複雜，所以我們不會在此提供技術解釋。相反，我們將觸及一些關於如何和為什麼計算它們的直覺。

零知識證明涉及證明關於多項式的聲明。多項式是一個類似f(x) = x² + 3 x + 1 的函數。在零知識證明中，驗證者證明他們擁有一些秘密信息的方式是，證明他們知道一個給定的多項式的輸入，而這個輸入可以求值到一個給定的輸出。例如，驗證者可能被賦予上述多項式，並被要求找到一個使輸出等於11 的輸入（答案是x = 2 ）。雖然這個任務對於小多項式來說是微不足道的，但是當給定的多項式非常大時，它就變得很有挑戰性。事實上，零知識證明的整個基礎是，這項任務對於大多項式來說是如此困難，以至於驗證者將無法重複找到答案，除非他們知道秘密見證。

那麼一個必要的步驟就是對多項式進行評估，以證明它等於某個輸出。在零知識中，這些多項式是由算術電路表示的。

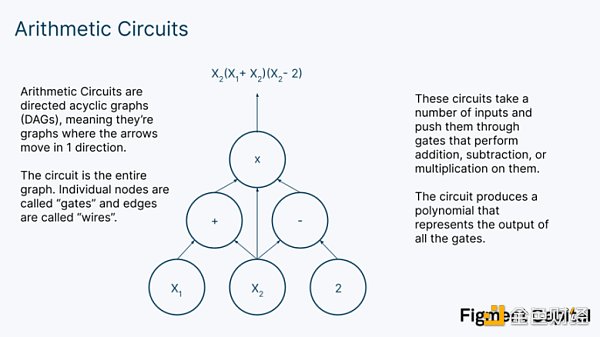
算術電路接受一個輸入矢量，並產生一個在這些點上評估的多項式。算術電路的大小因應用而大不相同，從~ 10000 到超過1000000.

我們可以通過插入一個數字併計算其輸出來直接評估一個多項式。這裡有一個例子：

這種方法被稱為直接評估，也是多項式的典型評估方式。問題是，直接求值的計算成本很高——它需要N² 次運算，其中N 是多項式的度數。因此，雖然這對小的多項式來說不是問題，但在處理大的算術電路時，直接評估會變得非常大。 NTT 解決了這個問題。通過利用非常大的多項式評估背後的模式，NTT 可以評估一項多項式，只需進行N*log(N) 計算。

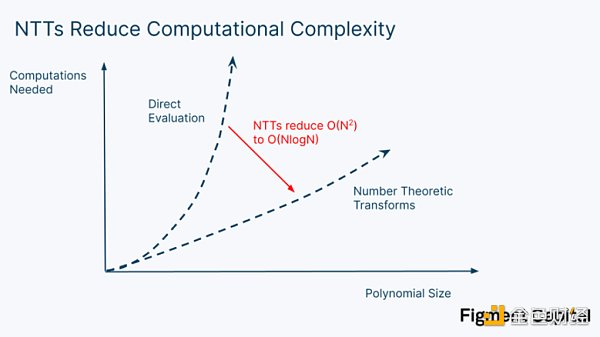
如果我們要評估一個度數為100 萬的多項式（意味著多項式中的最高指數為100 萬），直接評估需要1 萬億次操作。用NTT 計算同樣的多項式，只需要2000 萬次操作——速度提高了5 萬倍。

總之，評估多項式在零知識證明生成中起著關鍵作用，NTT 使我們能夠更有效地評估多項式。然而，即使採用這種技術，大型NTT 的處理時間仍然是零知識證明生成的主要瓶頸。

零知識硬件

我們已經對零知識證明加速的最重要的計算做了一個高層次的概述。算法上的改進，如用於MSM 的水桶法和用於評估多項式的NTT，導致了零知識證明時間的重大進步。但要進一步提高零知識證明性能，我們必須優化底層硬件。

加速MSM 和NTT 的發展

正如我們用水桶法所證明的那樣，MSM 很容易被並行化。然而，即使在嚴重並行化的情況下，計算時間仍然很長。此外，MSM 有大量的內存需求，因為需要存儲所有被操作的EC 值。因此，儘管MSM 具有在硬件上加速的潛力，但它們需要巨大的內存和並行計算。

NTT 對硬件不太友好。最重要的是，它們需要頻繁地將數據洗進洗出外部存儲器。數據是以隨機訪問模式從內存中檢索的，這就增加了數據傳輸時間的延遲。隨機內存訪問和數據洗牌成為一個主要瓶頸，限制了NTT 的並行化能力。大多數關於加速NTT 的工作都集中在管理計算與內存的互動方式上。例如，這篇來自Jump 的論文描述了一種方法，通過減少需要訪問內存的次數和將數據流向計算機芯片，從而加速NTT，將內存訪問延遲降到最低。

解決MSM 和NTT 瓶頸的最簡單方法是完全消除該操作。事實上，最近的一些工作，如Hyperplonk 引入了對Plonk 的修改，取消了執行NTT 的需要。這使得Hyperplonk 的加速更簡單，但是引入了新的瓶頸，比如昂貴的sumcheck 協議。在光譜的另一端，STARK 不需要MSM，也提供了一個更簡單的優化問題。

然而，加速MSM 和NTT 僅僅是零知識加速的第一步。即使我們可以假設將MSM 和NTT 的計算時間降至0 ，我們也只能實現證明生成時間的5-20 倍加速。這是由於阿姆達爾定律，該定律指出，加速度受我們實際進行計算的時間部分的限制。如果MSM 和NTT 佔了90% 的證明時間，消除它們仍會留下10% 的證明時間。

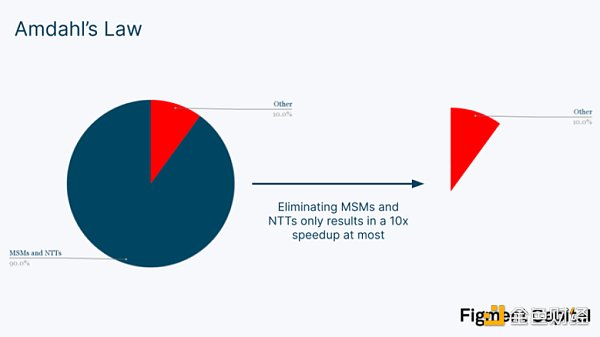
雖然加快MSM 和NTT 的速度很重要，但它們只是一個開始。為了取得進一步的進展，我們還必須加快「其他」操作，包括見證生成和散列。

硬件概述

有四種主要的計算機芯片類型： CPU、GPU、FPGA 和ASIC. 每種芯片在其結構、性能和通用性方面都有不同的權衡。

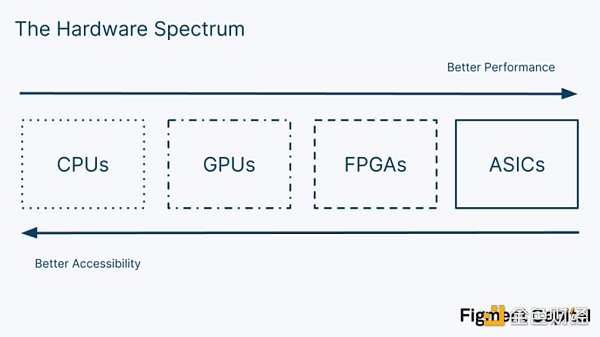
中央處理單元（CPU）是大多數消費類電子產品如筆記本電腦中的芯片。它們的通用性使它們很適合用於各種設備和日常任務。高通用性是以犧牲性能為代價的。 CPU 只能按順序處理操作，使其在許多應用中表現不佳。

圖形處理單元（GPU）是一種更專業的芯片。它們有大量的內核用於並行處理，使它們特別適合於圖形渲染和機器學習等應用。儘管沒有CPU 那麼普遍，也沒有FPGA 或ASIC 那麼專業，但GPU 是一種普遍的、可獲得的硬件。它們的流行導致了像CUDA 和OpenCL 這樣的低級庫的發展，幫助開發者利用GPU 的可並行性，而不需要了解底層硬件。

現場可編程門陣列（FPGA）是可定制的芯片，可以以可重複使用的方式為特定的應用進行優化。開發人員可以使用硬件描述語言（HDL）直接對其硬件進行編程，從而實現更高的性能。硬件可以被反復修改，而不需要新的芯片。 FPGA 的缺點是其更大的技術複雜性——很少有開發者有編程經驗。即使擁有必要的專業知識，定制FPGA 的研究和開發成本也很高。儘管如此，FPGA 在從國防科技到電信等行業都有應用。

特定應用集成電路（ASIC）是為某一特定任務過度優化的定制設計芯片。與允許硬件重新編程的FPGA 不同，ASIC 的規格是根植於芯片中的，防止它們被重新利用。對於任何特定的任務，ASIC 都是最強大和最節能的芯片。例如，比特幣挖礦是由ASIC 主導的，它計算的哈希值遠遠多於其他類型的芯片。

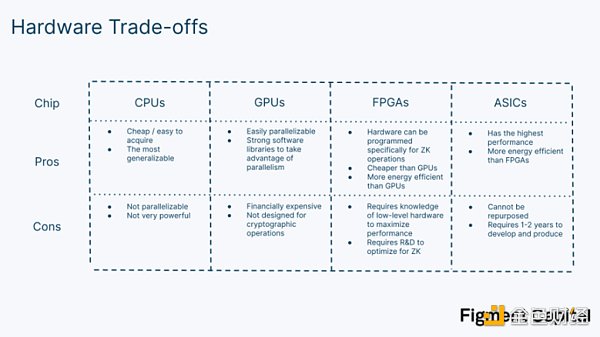
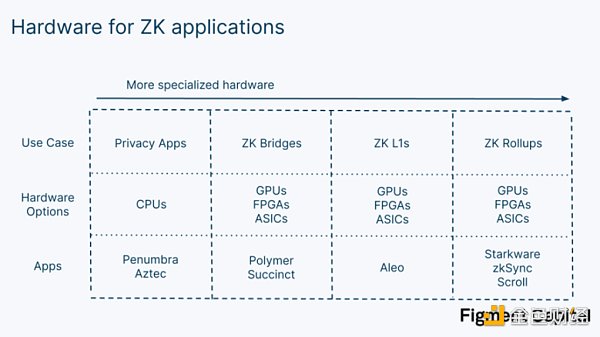
鑑於這些選擇，哪一個是最好的零知識證明成？這取決於應用程序。像Penumbra 和Aztec 這樣的隱私應用程序允許用戶在提交給網絡之前，通過創建其交易的SNARK 來進行私人交易。由於所需的證明相對較小，只需使用他們的CPU 就可以在他們的本地瀏覽器中生成。但對於真正需要硬件加速的較大的零知識證明，CPU 是不夠的。

硬件加速

我們可以通過多種方式在硬件上加速零知識證明：

• 並行處理：同時進行獨立計算。

• 管線： 確保我們的計算機的所有資源在任何時候都被使用，以最大限度地提高我們在一個時鐘週期內的計算量。

• 超頻： 將硬件的時鐘速度提高到超過默認速度，以加速計算。如果不小心這樣做，可能會損壞硬件。

• 增加內存帶寬：使用更高帶寬的內存來提高我們讀寫數據的速度。在零知識中，證明生成的瓶頸往往不是計算，而是數據的傳遞。

• 在內存中實現對大整數的更好表示： GPU 被設計為在浮點數（即十進制數字）上進行計算。零知識運算是在有限域的大整數上進行的。在內存中實現對這些大整數的更好表示，可以減少內存需求和數據洗牌。

• 使內存訪問模式可預測： 像PipeZK 這樣的論文探討了在計算NTT 的同時使內存訪問模式可預測的方法，使其更容易並行化。

任何類型的芯片都可以被流水線化和超頻。 GPU 非常適合併行化，但它們的架構是固定的；開發者被限制在所提供的內核和內存上。 GPU 不能為大整數創造更好的表示方法，也不能使內存訪問模式更可預測。雖然CUDA 和OpenCL 等GPU 庫提供了一定程度的靈活性，但硬件有局限性；更高的性能最終需要更靈活的硬件。儘管如此，GPU 仍然可以加速零知識證明。零知識硬件加速公司Ingonyama 正在建立ICICLE，這是一個用CUDA 為Nvidia GPU 建立的零知識加速庫。該庫包含加速常見零知識操作的工具，如MSM 和NTT.

FPGA 的時鐘速度比GPU 低，但可以通過編程來解決上述所有的加速策略。他們最大的問題只是對其進行編程。對於零知識來說，組織一個既有密碼學專業知識又有FPGA 工程專業知識的團隊是非常困難的。早期為零知識加速生產FPGA 的團隊是像Jump Crypto 和Jane Street 這樣已經擁有FPGA 和密碼學人才的複雜交易公司。 FPGA 也仍然有瓶頸——單個FPGA 往往沒有足夠的片上存儲器來執行NTT，需要額外的外部存儲器。

將硬件驅動的零知識速商業化的最嚴格的嘗試，甚至比單片FPGA 更進一步。為了獲得進一步的收益，像Cysic 和Ulvetanna 這樣的公司正在建立FPGA 服務器和FPGA 集群，結合多個FPGA 提供額外的存儲器和可並行計算，以進一步加速證明生成。這些團隊的早期結果是有希望的： Cysic 聲稱他們的FPGA 服務器在MSM 比Jump 的FPGA 架構快100 倍，在NTT 比最知名的GPU 實現快13 倍。標準化的基準還沒有建立起來，但結果指向了重大改進。

ASIC 能夠為零知識證明生成提供絕對最高的性能。今天的ZK ASIC 的問題是，他們正在為一個移動的目標進行優化——零知識正在迅速發展。由於ASIC 需要1 – 2 年和1000 – 2000 萬美元來生產，他們必須等到零知識已經足夠穩固，所生產的芯片不會很快被淘汰。另外，零知識證明的市場規模在未來幾年才變得足夠大，足以證明ASIC 所需的資本投資是合理的。

FPGA 和ASIC 之間有一個微妙的梯度。雖然FPGA 是可編程的，但它們的芯片有不可編程的硬化部分。固化部件的性能比可編程的要高得多。隨著零知識市場的發展，像Xilinx（AMD）和Altera（Intel）這樣的FPGA 公司可以生產新的FPGA，嵌入專門為零知識證明中的常見操作設計的硬化組件。同樣，ASIC 也可以被設計成包括一些靈活性。例如，Cysic 未來計劃生產專門針對MSM、NTT 和其他一般操作的ASIC，同時保持靈活性以適應許多證明系統。

從長遠來看，ASIC 將提供最強大的零知識證明加速功能。在此之前，我們預計FPGA 將服務於計算最密集的零知識用例，因為其可編程性使其能夠比GPU 更快地執行NTT、MSM 和其他加密操作。對於某些應用，GPU 將提供性能和可及性之間最具吸引力的平衡。

結論

區塊鏈行業多年來一直在等待零知識證明為生產做好準備。這項技術已經吸引了我們的想像力，承諾增強去中心化應用的可擴展性、隱私和互操作性。直到最近，該技術還不現實，主要是由於硬件限制和漫長的證明時間。這種情況正在迅速改變：零知識證明方案和硬件的進步正在解決MSM 和NTT 等計算瓶頸問題。有了更好的算法和更強大的硬件，我們可以將零知識證明加速到足以釋放其潛力，從而徹底改變Web3。

鳴謝： 特別感謝Brian Retford（RiscZero）、Leo Fan（Cysic）、Emanuele Cesena（Jump Crypto）、Mikhail Komarov（=nil; Foundation）、Anthony Rose（zkSync）、Will Wolf 和Luke Pearson（Polychain），以及Penumbra Labs 團隊的精彩討論和反饋，為本文做出了貢獻。

原文標題：Accelerating Zero-Knowledge Proofs

原文作者：Figment Capital

原文編譯：Lynn，MarsBit

來源：星球日報