TL;DR
我們提出OPML(Optimistic機器學習),它可以使用Optimistic方法對區塊鏈系統進行AI模型推理和訓練/微調。
與ZKML相比,OPML可以提供低成本、高效率的ML服務。 OPML的參與要求很低:我們現在能夠在沒有GPU的普通PC上運行帶有大型語言模型的OPML,例如7B-LLaMA(模型大小約為26GB)。
OPML採用驗證遊戲(類似於Truebit和Optimistic Rollup系統)來保證ML服務的去中心化和可驗證共識。
- 請求者首先啟動一個ML服務任務。
- 然後,服務器完成ML服務任務並將結果提交到鏈上。
- 驗證者將驗證結果。假設存在一個驗證者聲明結果是錯誤的。它通過與服務器的驗證遊戲(二分協議)啟動驗證遊戲,並試圖通過精確指出一個具體的錯誤步驟來反駁該聲明。
- 最後,在智能合約上進行單個步驟的仲裁。
單階段驗證遊戲
單階段精確定位協議的工作原理與計算委託(RDoC) 類似,其中假設兩個或多個參與方(至少有一個誠實的參與方)執行相同的程序。然後,雙方可以用精確的方式相互質疑,以找出有爭議的步驟。將步驟發送給計算能力較弱的法官(區塊鏈上的智能合約)進行仲裁。
在單階段OPML中:
- 我們構建了一個虛擬機(VM)用於鏈下執行和鏈上仲裁。我們保證了在智能合約上實現的鏈下VM和鏈上VM的等效性。
- 為了確保虛擬機中AI模型推理的效率,我們實現了一個專門為此目的設計的輕量級DNN庫,而不是依賴於流行的ML框架,如Tensorflow或PyTorch。此外,還提供了一個腳本,可以將Tensorflow和PyTorch模型轉換為這個輕量級庫。
- 採用交叉編譯技術將人工智能模型推理代碼編譯成虛擬機程序指令。
- 虛擬機鏡像是用默克爾樹管理的,只有默克爾根會被上傳到鏈上智能合約。 (默克爾根代表虛擬機狀態)
- 二分協議將幫助定位爭議步驟,該步驟將發送到區塊鏈上的仲裁合約
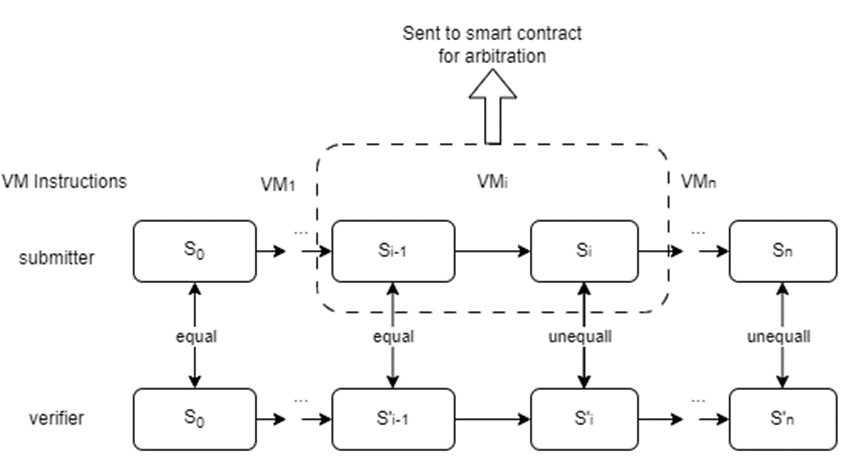
性能:我們在PC上測試了一個基本的AI模型(用於MNIST分類的DNN模型)。我們能夠在VM中2秒內完成DNN推理,在本地以太坊測試環境中,整個挑戰過程可以在2分鐘內完成。
多階段驗證遊戲
單階段精確定位協議的局限性
單階段驗證遊戲有一個嚴重的缺點:所有的計算必須在虛擬機(VM)內執行,這使我們無法充分利用GPU/TPU 加速或併行處理的潛力。因此,這一限制嚴重阻礙了大模型推理的效率,這也與當前RDoC協議的限制相一致。
過渡到多階段協議
為了解決單階段協議所帶來的限制,並確保OPML能夠達到與本機環境相當的性能水平,我們提出了對多階段協議的擴展。使用這種方法,我們只需要在最後階段在VM中進行計算,類似於單階段協議。對於其他階段,我們可以靈活地執行計算,從而在本機環境中實現狀態轉換,利用CPU、GPU、TPU甚至並行處理的能力。通過減少對VM的依賴,我們顯著地減少了開銷,從而顯著提高了OPML的執行性能,幾乎與本機環境類似。
下圖演示了一個驗證遊戲由兩個階段(k = 2)組成。在階段1中,該過程類似於一個單階段驗證遊戲,其中每個狀態轉換對應於一個改變虛擬機狀態的單個VM微指令。在階段2中,狀態轉換對應於包含改變計算上下文的多個微指令的“大指令”。
提交者和驗證者將首先使用二分協議啟動第二階段的驗證遊戲, 以定位“大指令”上的爭議步驟。此步驟將發送到下一階段,即phase -1。第一階段的工作原理類似於單階段驗證遊戲。第一階段的二分協議將有助於定位VM 微指令上的爭議步驟。該步驟將發送至區塊鏈上的仲裁合約。
為了確保過渡到下一階段的完整性和安全性,我們依賴於默克爾樹。該操作包括從更高級別的階段提取Merkle子樹,從而保證驗證過程的無縫延續。
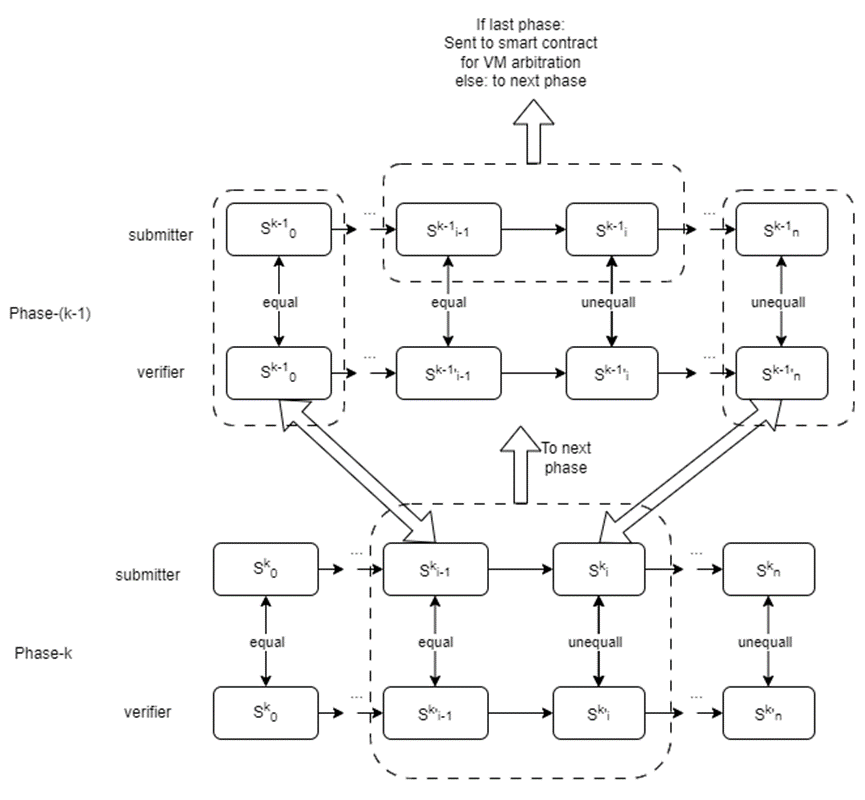
多階段OPML
在本演示中,我們提出了LLaMA 模型中使用的兩階段OPML 方法:
- 機器學習(ML),特別是深度神經網絡(DNN)的計算過程可以表示為計算圖,表示為G。該圖由各種計算節點組成,能夠存儲中間計算結果。
- DNN模型推理本質上是在上述計算圖上的計算過程。整個圖可以看作是推理狀態(Phase-2中的計算上下文)。在計算每個節點時,結果存儲在該節點中,從而將計算圖推進到下一個狀態。
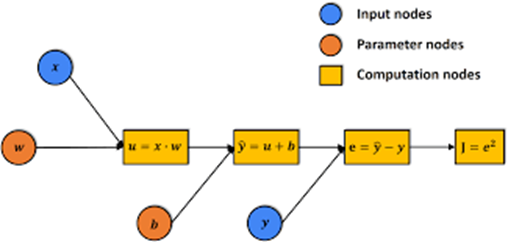
- 因此,我們可以先在計算圖上進行驗證博弈(在phase-2)。在第二階段驗證遊戲中,圖形節點的計算可以在本地環境中使用多線程CPU或GPU進行。二分協議將幫助定位爭議節點,該節點的計算將發送到下一階段(phase-1) 二分協議。
- 在第一階段二分中,我們將單個節點的計算轉換為虛擬機(VM)指令,類似於在單階段協議中所做的操作。
值得注意的是,當計算圖中單個節點的計算仍然計算複雜時,我們預計會引入多階段OPML方法(包括兩個以上階段)。這一延長將進一步提高驗證過程的整體效率和有效性。
性能改進
在這裡,我們對我們提出的多階段驗證框架進行了簡要的討論和分析。
假設有n DNN計算圖中的節點,每個節點需要取m VM微指令,在VM中完成計算。假設使用GPU或併行計算對每個節點的計算加速比為α 。該比率表示通過GPU或併行計算實現的加速,並且可以達到顯著值,通常比VM執行速度快幾十倍甚至數百倍。
基於這些考慮,我們得出以下結論:
1.兩階段OPML優於單階段OPML,實現了計算加速α次。多階段驗證的使用使我們能夠利用GPU或併行處理提供的加速計算能力,從而顯著提高整體性能。
2.當比較Merkle樹的大小時,我們發現在兩階段OPML中,大小為O(m+n),而在單階段OPML中,尺寸明顯大於O(mn)。 Merkle樹大小的減小進一步突出了多階段設計的效率和可擴展性。
總之,多階段驗證框架提供了顯著的性能改進,確保更高效和更快的計算,特別是在利用GPU或併行處理的加速能力時。此外,減小的Merkle樹大小增加了系統的有效性和可擴展性,使多階段OPML成為各種應用的選擇。
一致性與確定性
在OPML中,確保ML結果的一致性是至關重要的。
在DNN計算的本機執行過程中,特別是在不同的硬件平台上,由於浮點數的特性,可能會產生執行結果的差異。例如,涉及浮點數的並行計算,例如(a+b)+c與a+(b+c), 由於舍入誤差,通常會產生不相同的結果。此外,編程語言、編譯器版本和操作系統等因素都可能影響浮點數的計算結果,從而導致ML結果進一步不一致。
為了應對這些挑戰並保證OPML的一致性,我們採用了兩種關鍵方法:
1.採用定點算法,又稱量化技術。這種技術使我們能夠使用固定精度而不是浮點數來表示和執行計算。通過這樣做,我們減輕了浮點舍入誤差的影響,從而獲得更可靠和一致的結果。
2.我們利用基於軟件的浮點庫,這些庫旨在跨不同平台保持一致的功能。這些庫確保了ML結果的跨平台一致性和確定性,而無論底層硬件或軟件配置如何。
通過結合定點算法和基於軟件的浮點庫,我們為在OPML框架內實現一致和可靠的ML結果奠定了堅實的基礎。這種技術的協調使我們能夠克服浮點變量和平台差異帶來的固有挑戰,最終增強OPML計算的完整性和可靠性。
OPML vs ZKML
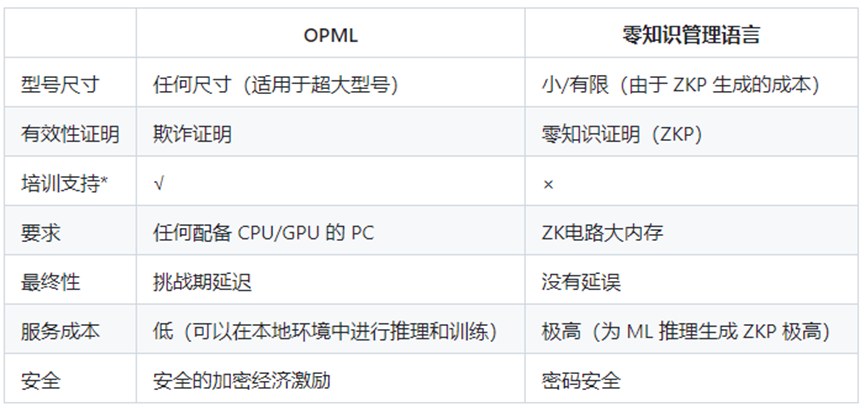
*:在當前的OPML框架中,我們的主要重點在於ML模型的推理,從而實現高效且安全的模型計算。然而,必須強調的是,我們的框架也支持訓練過程,使其成為各種機器學習任務的通用解決方案。
請注意,OPML仍在開發中。如果您有興趣成為這一激動人心的計劃的一部分,並為OPML項目做出貢獻,請隨時與我們聯繫。


