編譯:Antalpha Labs
今天,我們與Panoptic 的Guillaume Lambert 以及Bancor / Carbon 的Mark Richardson 進行了一次非常有趣的討論,主題涉及提供流動性(lp)、交易和自動做市商(AMM)。我想在這裡簡要地提出一些我已經思考了一段時間的想法,這些想法相互關聯,但是我也不是非常確定他們如何應用。
譯註:Guillaume Lambert 是在twitter 和medium 以及uniswap 社群中非常活躍的教授,有自己的專案Panoptic ,對lp 與選擇權的相關討論也非常多。
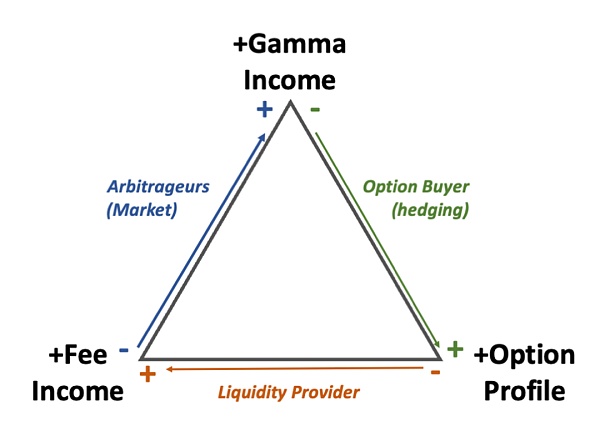
我想描述的關鍵概念,是我想稱之為”AMM三角形”的東西,一方面它代表了AMM(自動做市商)中不同參與者之間的關係(流動性提供者和套利者),另一方面是選擇權交易者(特別是對沖選擇權買家)。讓我們先從這個三角形開始:
AMM 三角
這個概念代表了與AMM(自動做市商)部位相關的三個價值流(暫時沒有更好的字眼來描述):
-
流動性提供者每次在AMM 上進行交易時收到的手續費
-
與無常損失相對應的選擇權組合,這裡考慮的是擁有一個看漲期權(與鏈接[1]中所述的平方根配置相符)的投資組合。
-
與選擇權配置對沖以及AMM 頭寸再平衡相對應的 Gamma 收入
譯註:這裡的開平方指的是,例如eth -u 的uniswap 部位的價值和eth-u 價格關係是開平方的關係。這個會在後續的文章中單獨補充說明。 call 選擇權也是廣義選擇權。
我們現在確定了三種典型的市場參與者,每一種都佔據了三角形的一條邊,這意味著他們在相應的頂點上是空頭,而在其他地方是多頭。更詳細地說:
-
流動性提供者獲得費用收入,但是做空對應選擇權組合,後者包含無常損失[2]和相對應的平方根選擇權收益[3]
-
套利者是交易手續費的收入的空頭,但是他們能獲得與無常損失相對應的gamma 收入
-
選擇權交易者長期持有選擇權組合併對其進行對沖,因此對gamma 收入持有空頭部位。
我在theammbook.org[4]論文的AMMs和金融衍生品[5]章節中詳細討論了這些主題,這裡只給出高層次的直覺。
流動性提供者的處境:AMM 在設計上給予其手續費,k=x*y 的恆定積的AMM 的無常損失損失對應的平方根期權對應已經研究的差不多了,同樣,集中流動性的期權特性也對應於流動性範圍內的選擇權組合。
套利者是交易手續費的空頭——這就是你在AMM 上交易時要支付的費用。可能不完全明顯的是,他們還是gamma 的多頭。要理解這一點,關鍵的訊息是,套利者的交易使價格從P0 移動到P1,平均成交價格是幾何平均sqrt(P0*P1)。這意味著什麼呢?讓我們使用標準的假設,沒有最終客戶,市場深度大且流動性好,套利者在該市場和AMM 之間進行交易。在這種情況下,眾所周知,AMMs 將被持續套利,使其邊際價格對應於市場價格。那麼,當價格從P0 移動到P1 並返回時會發生什麼?正如我們之前看到的,AMM 以相同的價格買入和賣出,即幾何平均數。然而,套利者已經以P0 的價格買入,並以P1 的價格賣出,即捕獲了完整的市場移動——這就是他們的“gamma 收入”,並且可以輕易地證明,這個伽馬確實對應於AMMs 的「暫時性損失」收益概況。
對於期權交易者來說,同樣地眾所周知:如果交易者持有一個期權概況並進行delta 對沖,那麼——當然只在理想的Black Scholes 世界中——他們的delta 對沖成本正好是他們在到期時的收益。
這個模型有一些基本的缺陷需要了解,部分原因是套利者和交易者都是在非常理想化的市場環境中被討論的,這其中存在一些基本的問題,例如:
-
如果有一個深度和流動性都很好的市場,我們為什麼需要AMMs?為什麼人們不都在那個深度和流動性好的市場上交易?
-
世界並不是一個Black Scholes 世界,delta 對沖並不是一個完美的複製策略
-
套利者有選擇不交易的權利,所以他們只會在他們的gamma 收入高於他們支付的費用時參與;伽馬等同於期權到期收益,因此費用永遠不能補償暫時性損失
現實是,市場微觀結構比Black Scholes 和深度-流動市場假設所暗示的要豐富得多,在現實世界中,每個人都有他們的位置。然而——在我看來,AMM 三角形給出了一個很好的結構性指示,說明了這些不同方面是如何相互關聯的,以及如何結合它們來提取某些特定的流動性,特別是與期權相關的流動性。