原創:劉教鏈
一片花飛減卻春,風飄萬點正愁人。且看欲盡花經眼,莫厭傷多酒入唇。
五月的加密市場,BTC(比特幣)在6萬刀踟躕不前,春去花落一片紅。無甚熱鬧,但徜徉湖邊,看綠水青山,心底寧靜,部位致遠。
BTC乃加密產業之根。總量2100萬之上限,乃BTC之本。一切都從這個神奇的數字展開。可是它,為何是這樣一個數字呢?
教鏈在2020年12月5日文章《為什麼比特幣最多只會有2,100萬枚? 》中,就曾介紹過這個數字的計算方法。簡而言之是這樣的:
1. 每區塊產量50 BTC
2. 每21萬個區塊,產量減半
使用等比數列求和可以輕鬆算出,最終BTC的總產量為:(50 + 25 + 12.5 + 6.25 + 3.125 + …) x 21萬= 2100萬枚。
進一步的,調節「挖礦」難度使得大約每10分鐘產生一個新區塊,即每小時6個新區塊,21萬個區塊就大概是人間4年。
這也就是比特幣4年產量減半週期的來歷。
但是,如此只是對既定事實的鋪敘而已。一是缺乏一些細節的考察;二是並未真正揭示比特幣發明人中本聰為何要選擇和設計這樣一個數字的原因。
先說細節。
首先,2,100萬並非2,100萬,而是2,099,999,997,690,000。對,後面這個數字比2,100萬大1億倍,約是2,100兆。在比特幣系統內部,都是這個兆級的整數。
當我們把BTC「展示」為這個整數點上8位小數位,也就變成了2 0,99 9,99 9.97 690 000。這裡我用空格提示了上面當整數時的千分位分割點。我們一眼就會看到,中本聰選擇8位小數位其實有些奇怪的,因為這樣會導致8位小數的BTC整數部分的逗號分割點,和系統內真正的整數的逗號分割點不一致。
8位小數位,也就是1億分之一,這個就不太西方。眾所周知,英文裡對數字採用千分位分割,所以計數法的單位是千(thousand)、百萬(million)、十億(billion)、萬億(trillion)。英文裡並沒有「億」這個單位。而中國的計數法略有不同,是以4位數字也就是萬分位為分割的,乃有萬、億、萬億。
2100兆用萬分位分割就是這樣的:2099 9999 9769 0000;2100萬帶8位小數則是這樣的:2099 9999.9769 0000。都是4小節,每小節4位數,沒有任何混亂。所以看起來,8位小數位,1億分之一,嗯,這很東方。
其次,2100兆之所以是2,099,999,997,690,000而不是精確的2,100,000,000,000,000,也正是因為8位小數位的精度限制。
上文的等比數列(50 + 25 + 12.5 + 6.25 + 3.125 + …)並非真正的無窮數列,而是當它減小到0.0000 0001之後,再減半就歸零了。因此,這是一個截斷了的有窮數列,其加和就要小於無窮數列求和的結果100。所以,乘以21萬之後,最終結果也要略小於2100萬。
第三,注意第一點的敘述,8位小數位和小數點只是一個「展示」層面的設計。在系統內部只有那個萬億級的整數。
既然只是“展示”,那麼其實小數點是可以任意挪動的。現在點在8位小數的位置,以後也可以點在5位或4位小數的位置。
例如,20,999,999,976.90000(5位小數),或2099 9999 9769.0000(4位小數)。
那麼,8位小數時的1枚比特幣,當移位到5位小數時,就顯示為1000,移位到4位小數時,就顯示為10000。對應的,原來的0.001或0.0001 BTC現在就會顯示為1。
這移位的想法並非教鏈杜撰的,而是中本聰真實的想法。2009年4月12日中本聰給Mike Hearn的回信[1]中,他這樣寫道:
“My choice for the number of coins and distribution schedule was an educated guess. It was a difficult choice, because once the network is going it’s locked in and we’re stuck with it。 existing currencies, but without knowing the future, that’s very hard. I ended up picking something in the middle. If Bitcoin remains a small niche, it’ll be worth less per unit than existing currencies。 of world commerce, then there’s only going to be 21 million coins for the whole world, so it would be worth much more per unit. Values are 64-bit integers with 8 decimal pers, unit. Values are 64-bit integers with 8 decimal 0s, 5 1 coin as 0. of granularity if typical prices become small. For example, if 0.001 is worth 1 Euro, then it might be easier to change where the decimal point is displayed, so if you had 1change where the decimal point is displayed, so if you had 1 .”
「我對硬幣數量和發行時間表的選擇是經過深思熟慮的。這是一個艱難的選擇,因為一旦網路開始運行,它就會被鎖定,我們就會被它困住。我想選擇一種能讓價格與現有貨幣相近的(數字),但在不知道未來的情況下,這很難做到。就會低於現有貨幣。位元整數,因此1 枚硬幣在內部表示為100000000。和使用),所以如果你有1 個比特幣,現在顯示為1000,而0.001 顯示為1。
有人說,對於普遍的64位元電腦而言,如果我們使用64位元二進制數同時表示整數和小數(又稱浮點數),那麼最安全的做法是把整數限制在浮點數的整數部分可表達的上限內。
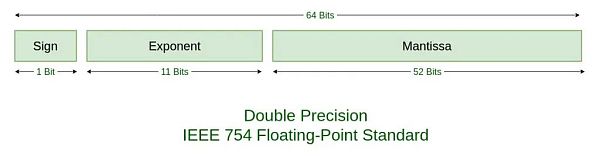
稍微了解電腦原理的朋友都知道,電腦內部並沒有什麼小數,都是0和1的數位。所謂64位元整數,就是指64個0或1所組成的二進位整數。對應10進位就是2^64 = 18446744073709551616。這個數字要遠大於2100兆。但是,如果要讓電腦能夠處理浮點數,那麼就要把64位元中拆出一部分用來表示小數部分,還要留出1位元來表示正負號。這就成了IEEE 754浮點數編碼標準。其中標準定義,雙精確度浮點數用64位元二進位是這樣編碼的:
這樣一來,整數部分就只能使用53位,也就是最大不超過2^53 = 9007199254740992。而如果希望容易測試結果是否為整數,則最好不要超過2^51 = 2251799813685248。如此,可以選擇22(百萬億),但22不是一個「三角數」(triangular number),所以中本聰選擇了21(百萬億)。

據此許多人認為中本聰選擇2100萬億,大大方便了各種程式語言處理比特幣數量相關的計算。
不過,教鏈看了中本聰的郵件後,覺得中本聰或許並沒有這麼複雜的想法。或者他的確思忖過,但是並沒有講透他的全盤考慮。他只是講,也曾經考慮過其他數字,比如4200萬億,但是感覺太大了,於是就折中成了2100萬億。2011年1月10日中本聰回覆Mike Hearn的郵件[2]中,他是這樣寫的:
“It works out to an even 10 minutes per block:
21000000 / (50 BTC * 24hrs * 365days * 4years * 2) = 5.99 blocks/hour
“I fudged it to 364.58333 days/year. The halving of 50 BTC to 25 BTC is after 210000 blocks or around 3.9954 years, which is approximate anyway based on the retsgainst’m’t’t’t 面’
“I thought about 100 BTC and 42 million, but 42 million seemed high.
“I wanted typical amounts to be in a familiar range. If you’re tossing around 100000 units, it doesn’t feel scarce. The brain is better able to work with numbers from 0.01 to 10000.
“If it gets really big, the decimal can move two places and cents become the new coins.”
看起來,中本聰是先定了時間諸參數,而後調整區塊產量和總量,並思考多大的數字較為適合。
依中本聰的意思,大多數人手上的BTC數量最好在0.01到1000之間,不要動輒就搞個6、7位數的幣,那樣會缺乏稀缺感。
以上就是關於2100萬枚總量數字的來龍去脈。